A tuning fork is in unison with 1.0 m length of sonometer wire. When the stretching weights are immersed in water, the length of the wire in unison with the same tuning fork is 0.934 m. Calculate the density of the material of the weights ?
The correct Answer is: Relative density =. Density
To solve the problem, we will follow these steps:
Step 1: Understand the relationship between frequency and length of the wire
The frequency of a vibrating string (or wire) is given by the formula:
f=12L√Wm
where:
- f is the frequency,
- L is the length of the wire,
- W is the weight (force due to gravity on the weights),
- m is the mass of the wire.
Step 2: Set up the equations for the two lengths
Given:
- Length L1=1.0m
- Length L2=0.934m
Since the tuning fork is in unison with both lengths, we can set up two equations using the frequency formula:
1. For L1:
f1=12L1√W1m
2. For L2:
f2=12L2√W2m
Step 3: Equate the frequencies
Since f1=f2, we can set the two equations equal to each other:
12L1√W1m=12L2√W2m
Step 4: Simplify the equation
Cancel out the common terms:
1L1√W1=1L2√W2
Rearranging gives:
√W1√W2=L1L2
Step 5: Substitute the known lengths
Substituting L1=1.0m and L2=0.934m:
√W1√W2=1.00.934
Step 6: Square both sides
Squaring both sides gives:
W1W2=(1.00.934)2
Calculating this:
W1W2≈1.146
Step 7: Relate the weights to density
The density ρ of the weights can be calculated using the formula:
ρ=WV
where V is the volume of the weights. The volume can be expressed in terms of the weight and density of water (since the weights are immersed in water):
V=Wρwater(where ρwater≈1000kg/m3)
Step 8: Calculate the density of the weights
Using the relationship between the weights:
Let W1=W and W2=W1.146
The relative density of the weights can be expressed as:
Relative Density=W1W1−W2=WW−W1.146=11−11.146≈7.849
Step 9: Convert to kg/m³
To convert from grams per cubic meter to kilograms per cubic meter:
ρ≈7.849×103kg/m3
Final Answer
The density of the material of the weights is approximately:
ρ≈7849kg/m3
---
The frequency of a vibrating string (or wire) is given by the formula:
f=12L√Wm
where:
- f is the frequency,
- L is the length of the wire,
- W is the weight (force due to gravity on the weights),
- m is the mass of the wire.
Given:
- Length L1=1.0m
- Length L2=0.934m
f1=12L1√W1m
f2=12L2√W2m
Since f1=f2, we can set the two equations equal to each other:
12L1√W1m=12L2√W2m
Cancel out the common terms:
1L1√W1=1L2√W2
√W1√W2=L1L2
Substituting L1=1.0m and L2=0.934m:
√W1√W2=1.00.934
Squaring both sides gives:
W1W2=(1.00.934)2
Calculating this:
W1W2≈1.146
The density ρ of the weights can be calculated using the formula:
ρ=WV
where V is the volume of the weights. The volume can be expressed in terms of the weight and density of water (since the weights are immersed in water):
V=Wρwater(where ρwater≈1000kg/m3)
Using the relationship between the weights:
Let W1=W and W2=W1.146
The relative density of the weights can be expressed as:
Relative Density=W1W1−W2=WW−W1.146=11−11.146≈7.849
To convert from grams per cubic meter to kilograms per cubic meter:
ρ≈7.849×103kg/m3
The density of the material of the weights is approximately:
ρ≈7849kg/m3
Topper's Solved these Questions
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - From Organ Pipes
22 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - From Beats
15 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Selected Problems (From Wave Equation, Intensity , Energy Density)
24 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS
79 Videos
Similar Questions
An iron load of 2Kg is suspended in the air from the free end of a sonometer wire of length 1m.A tuning frok of frequency 256 Hz, is in resonace with 1√7 times the length of the sonometer wire. If the looad is immersed in water, the length of the wire in metre that will be in resonance with the same tuning fork is (specific gravity of iron=8)
View SolutionA stone is hung in air from a wire which is stretched over a sonometer. The bridges of the sonometer are L cm apart when the wire is in unison with a tuning fork of frequency N . When the stone is completely immersed in water, the length between the bridges is l cm for re-establishing unison, the specific gravity of the material of the stone is
View SolutionA stone in hung in air from a wire which is stretched over a sonometer . The bridges of the sonometer are 40cm apart when the wire is in unison with a tuning fork of frequency 256Hz. When the stone is completely immersed in water , the length between the bridges is 22cm for re - establishing unison . The specific gravity of the material of the stone is
View SolutionA tuning fork is in unison with a sonometer wire 80 cm long. If 2 beats are heard on shortening the wire by one centimeter find the frequency of the fork?
View SolutionTwo tuning forks produce 5beats when sounded together.A is in unison with 40cm length of a sonometer wire under a constant tension and B is in unison with the same wire of length 40.5cm under the same tension. Calculate fundamental frequency of the forks.
View SolutionA string is stretched by a block going over a pulley . The string vibrates in its fifth harmonic in unison with a particular tuning fork . When a beaker containing a liquid of density ρ is brought under the block so that the block is completely dipped into the beaker , the string vibrates in its seventh harmonic in unison with the tuning fork . Find the density of the material of the block.
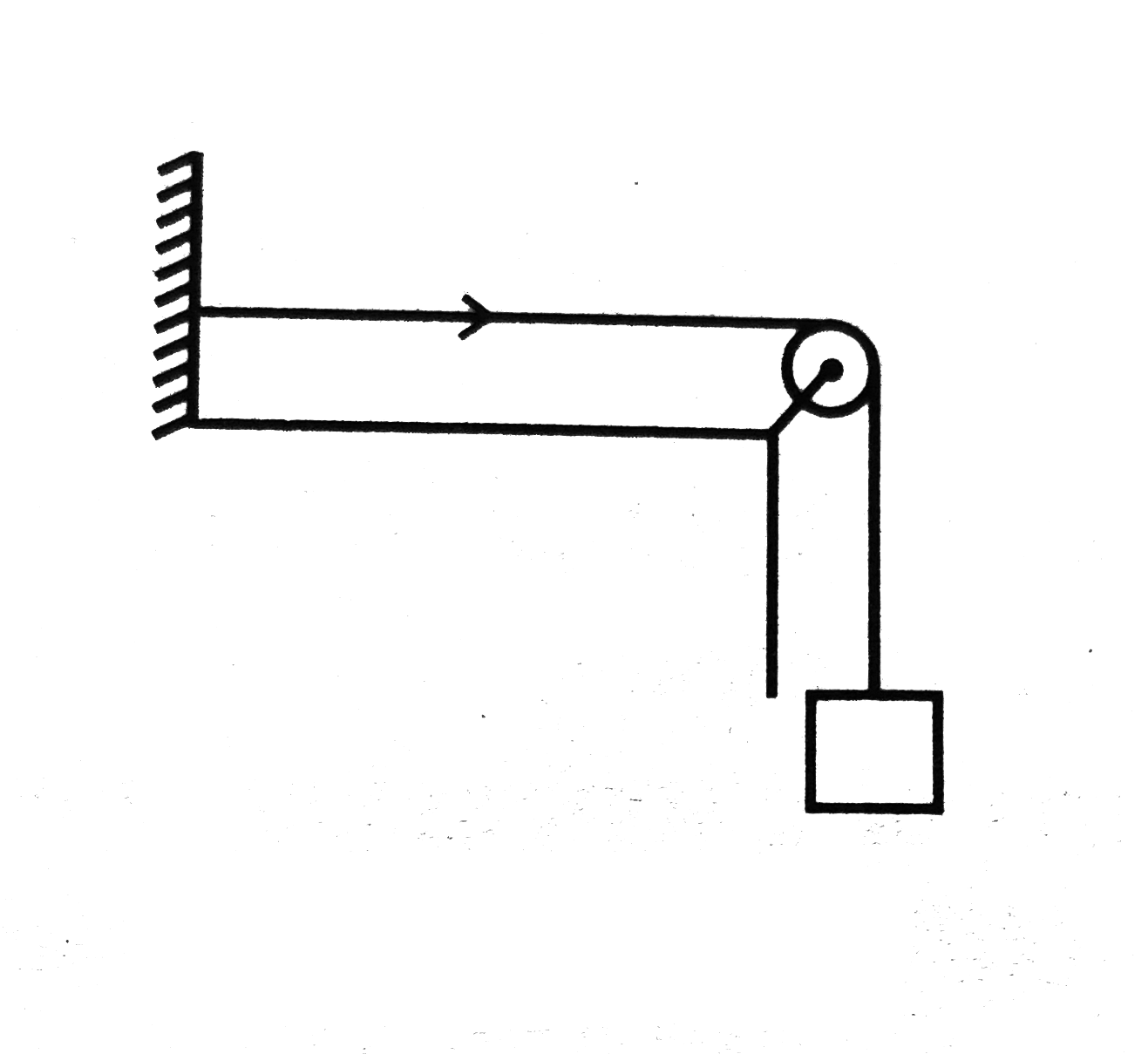
View SolutionTwo forks A and B when sounded together produce 4 beat/s. The fork A is in unison with 30 cm length of a sonometer wire and B is in unison with 25 cm length of the same wire at the same tension Calculate the frequency of the forks.
View SolutionIn the sonometer experiment , a tuning fork of frequency 256Hz is in resonance with 0.4m length of the wire when the iron load attached to free end of wire is 2kg. If the load is immersed in water , the length of the wire in resonance would be ( specific gravity of iron =8)
View SolutionA wire is suspended vertically from a rigid support. When loaded with a steel weight in air, the wire extends by 16cm. When the weight is completely immersed in Water, the extension is reduced to 14cm. The relative density of the material of the weight is
View SolutionFor definite length of wire, if the weight used for applying tension is immersed in water , then frequency will
View Solution
