The distance between the toothed wheel with 720 teeth and the mirror in the Fizeau experiment is 7.0 km. Two consecutive rotation speeds of the wheel for which the light disappeared were 283 r.p.s and 313 r.p.s .Find the velocity of light.
The correct Answer is: m//s
The transit time of the light pulse from the light pulse from the toothed wheel to the mirror and back is . During this time the toothed wheel rotating at = 313 r.p.s. will turn through k + 1 teeth, so k + teeth, so k + 1 . Subtracting we obtain 1 = .from which
Similar Questions
The distance beween the toothed wheel with 720 teeth and the mirror in an experiment based on Fizeau's method is 7 km. The two consecutive speeds of rotation of the wheel for which light disappeared were 283 rps and 313 rps. Find the velocity of light.
View SolutionIn the Fizeau experiment on measurement of the velocity of light the distance between the gear wheel and the mirror is l=7.0km, the number of teeth is z=720. Two successive disappearances of light are observed at the folllowing rotation velocities of the wheel: n1=283rps and n2=313 rps. Find the velocity of light.
View Solution
Knowledge Check
If the distance between two cities P and Q is more than the distance between another two cities R and S (the speeds of mode of transport used is same for both), then
Atime taken will be more in travelling from P to Q than from R to SBtime taken will be more in travelling from R to S than from P to QCtime taken will be same in both journeysDdata insufficient.In Young’s double slit experiment, the distance between slits and screen is 2 m and distance between slits is 0.25 mm. A light of wavelength 800 nm is used to find fringes on the screen. If screen moves with a speed of 5 m/s, then first maxima will move with a speed of
A16 mm/sB8 mm/sC20 m/sD50 mm/s
In a biprism experiment , a monochromatic light of wavelength 6×10−7 m is used . The distance between the slit and the prism is 10 cm and that between the biprism and the eyepiece is 65 cm . If the distance between two consecutive dark bands is 0.03 m . calculate the distance between the two virtual images of the slits .
View SolutionIn Fizeau's experiment the distancec between the source and the reflector is 8 km and there are 720 teeth in the toothed wheel. At what speed would the first, second and third eclipses occur? (Velocity of light =3×109ms−1)
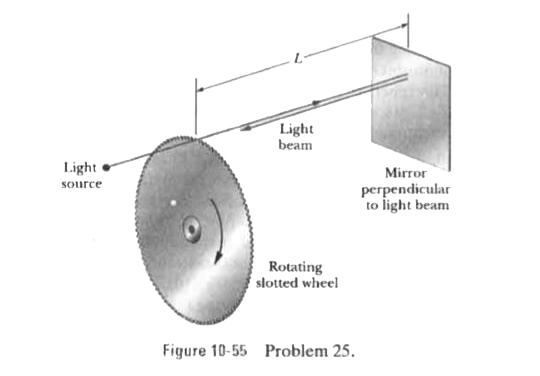
View SolutionFigure 10-55 shows an early method of measuring the speed of light that makes use of a rotating slotted wheel. A beam of light passes through one of the slots at the outside edge of the wheel, travels to a distant mirror, and returns to the wheel just in time to pass through the next slot in the wheel. One such slotted wheel has a radius of 5.0 cm and 500 slots around its edge. Measurements taken when the mirror is L = 500 m from the wheel indicate a speed of light of 3.0×105km/s. (a) What is the (constant) angular speed of the wheel? (b) What is the linear speed of a point on the edge of the wheel?
View SolutionIn an experiment with Foucault's apparatus, the various distances used are as follows :
Distance between the rotating and the fixed mirror = 16 m
Distance between the lens and the rotating mirror = 6 m,
Distance between the source and the lens = 2 m. When the mirror is rotated at a speed of 356 revolutions per second, the image shifts by 0.7 mm. Calculate the speed of light from these data.
View SolutionIn an experiment with Foucault's apparatus, the various distances used are as follows :
Distance between the rotating and the fixed mirror = 16 m
Distance between the lens and the rotating mirror = 6 m,
Distance between the source and the lens = 2 m. When the mirror is rotated at a speed of 356 revolutions per second, the image shifts by 0.7 mm. Calculate the speed of light from these data.
View SolutionA wheel of radius R rolls without slipping on the horizontal surface with speed v0. When the contact point is P on the road, a small patch of mud separates from the wheel at its highest point strikes the road at point Q. Find distance PQ.
View Solution
