Consider the 2-place Boolean function f:{0,1}→{0,1} defined by f(x1,x2)=x1+x2.x2 Then following f(0,1) is equal toSolution in Bengali
0
1
not defined
none of these
The correct Answer is:B
Step by step video, text & image solution for Consider the 2-place Boolean function f :{0,1} rarr{0,1} defined by f(x_1 , x_2)= x_1+x_2.x_2 Then following f(0,1) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
For a frequency distribution, mean deviation about mean is computed by
View SolutionFind the equation of the straight line which is perpendicular to y=x and passes through (3,2).
View SolutionIf f is a real valued function, not identically zeroand satisfying f(x_1 + x_2)) + f(x_1 - x_2) = 2 f(x_1)f(x_2)forall x_1,x_2 , then f(x) is (1) An odd function(2) An even function (3) Neither even nor odd(4) f(0) = 1/2
View SolutionIf |f(x1)−f(x2)|≤(x1−x2)2,∀x1,x2∈R. Find the equation of tangent to the curve y=f(x) at the point (1,2).
View SolutionFind the domain of definition of f(x)=loge.1−x1+x. Further show that,
f(x1)+f(x2)=f(x1+x21+x1x2),x1,x2∈(−1,1)
View SolutionI : If f(x) = cosh x + sinh x then f(x1+x2+...+xa)=f(x1)⋅f(x2)⋆f(xn)
II : If f(x) = cosh x + sinh x then f(x1)+f(x2)+...+f(xn)=f(x1)⋅f(x2)⋆f(xn)
View SolutionIn interval I if x_1 < x_2 and f(x_1) le f(x_2) for all x_1 , x_2 in I then f is
View SolutionIn interval I if x_1 f(x_2) for all x_1 , x_2 in I then f is
View Solutionf(x)=loge(1−x1+x) অপেক্ষকটির সংজ্ঞার ক্ষেত্র নির্ণয় করো। দেখাও যে , f(x1)+f(x2)=f(x1+x21+x1x2),x1,x2∈(−1,1)
View SolutionIf f:N→N,and x2>x1⇒f(x2)>f(x1) for x1,x2∈N a n df(f(n))=2n∀n∈N, then f(2)=_________
View Solutionif |f(x1)−f(x2)|≤(x1−x2)2Find the equation of tangent to the curve y=f(x) at the point (1,2).
View SolutionThe following functions are defined for the set of variables x1,x2,x3,.......,xn
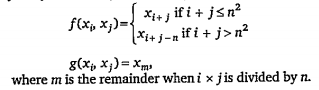
Find the value of f(f(x2,x3),f(x5,x6)) if n=3
View SolutionFind the domain of definition of f(x)=loge(1−x1+x) Further show thatf(x1)+f(x2)=f(x1+x21+x1x2),x1,x2∈(−1,1)
View SolutionIf y=f(x) is a curve and if there exists two points A(x1,f(x1)) and B(x2,f(x2)) on it such that f'(x1)=−1f(x2), then the tangent at x1 is normal at x2 for that curve. Number of such lines on the curve y=sinx is
View SolutionIF [x1x2y1y2]−[2301]=[3512] then determine x1,x2,y1,y2.
View Solution
