If limx→c−{lnx}andlimx→c+{lnx} exist finitely but they are not equal (where {.} denotes fractional part function), then:
c' can take only rational values
c' can take only irrational values
c' can take infinite values in which only one is irrational
c' can take infinite values I which only one is rational
The correct Answer is:D
To solve the problem, we need to analyze the limits of the fractional part of the natural logarithm function as x approaches c from the left and right. The fractional part function is denoted as {x}=x−⌊x⌋, where ⌊x⌋ is the greatest integer less than or equal to x.
1. Understanding the Limits:
We need to evaluate limx→c−{lnx} and limx→c+{lnx}. We know that these limits exist finitely but are not equal.
2. Choosing a Value for c:
Let's consider c=e (the base of the natural logarithm). As x approaches e from the left (c−):
lnx→lne=1(from the left)
Thus, limx→e−{lnx}={1}=1−0=1.
3. Evaluating the Right Limit:
As x approaches e from the right (c+):
lnx→lne=1(from the right)
Thus, limx→e+{lnx}={1}=0(since we take the fractional part).
4. Conclusion from the Limits:
We find that:
limx→e−{lnx}=1andlimx→e+{lnx}=0
Since these two limits exist but are not equal, we confirm the conditions of the problem.
5. Generalizing the Result:
This behavior can be generalized for other values of c that are positive and irrational. For rational values of c, the limits will also differ, but the key takeaway is that for irrational values of c, the limits will yield fractional parts that differ.
Final Answer:
The limits exist finitely but are not equal, indicating that c must be an irrational number.
We need to evaluate limx→c−{lnx} and limx→c+{lnx}. We know that these limits exist finitely but are not equal.
Let's consider c=e (the base of the natural logarithm). As x approaches e from the left (c−):
lnx→lne=1(from the left)
Thus, limx→e−{lnx}={1}=1−0=1.
As x approaches e from the right (c+):
lnx→lne=1(from the right)
Thus, limx→e+{lnx}={1}=0(since we take the fractional part).
We find that:
limx→e−{lnx}=1andlimx→e+{lnx}=0
Since these two limits exist but are not equal, we confirm the conditions of the problem.
This behavior can be generalized for other values of c that are positive and irrational. For rational values of c, the limits will also differ, but the key takeaway is that for irrational values of c, the limits will yield fractional parts that differ.
The limits exist finitely but are not equal, indicating that c must be an irrational number.
Topper's Solved these Questions
- LIMITBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - LIMITEXERCISE - EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)
24 Videos
- LIMITBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - LIMITEXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
7 Videos
- INVERSE TRIGONOMETRIC FUNTIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNTIONS EXERCISE - Exercise-5 : Subjective Type Problems
5 Videos
- LOGARITHMS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - LOGARITHMS EXERCISE - Exercise-5 : Subjective Type Problems
19 Videos
Similar Questions
The value of limx→0sin−1{x} (where {.} denotes fractional part of x) is
View Solutionlimx→1−e{x}−{x}−1{x}2 equal, where {.} is fractional part function and I is aan integer, to :
View Solutionlimx→cf(x) does not exist when
where [.] and {.} denotes greatest integer and fractional part of x
View SolutionIf both Limx→c−f(x) and Limx→c+f(x) exist finitely and are equal, then the function f is said to have removable discontinuity at x=c. If both the limits i.e. Limx→c−f(x) and Limx→c+f(x) exist finitely and are not equal, then the function f is said to have non-removable discontinuity at x=c.
Which of the following function not defined at x=0 has removable discontinuity at the origin?
View SolutionLet f(x)=limn→∞n2tan(ln(secxn))andg(x)=min(f(x),{x}}
(where {.} denotes fractional part function)
Left derivative of ϕ(x)=e√2f(x)atx=0 is:
View SolutionGraph of y=f(x) is shown in the adjacent figure
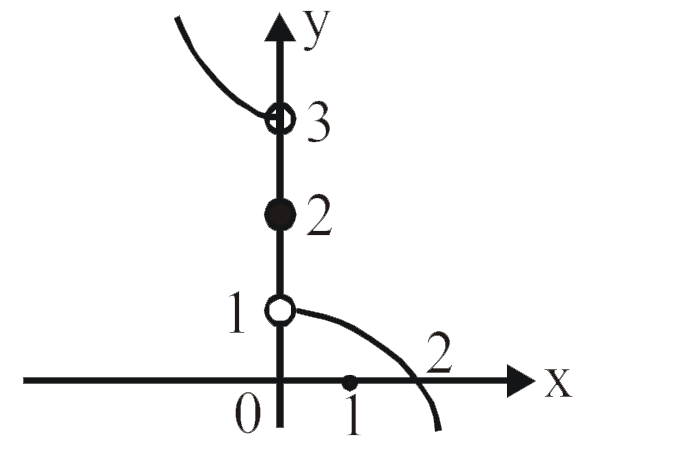
Value of lim0+({f(x)−1}) is equal to (wher {.} denotes fractional part function)
View Solutionlimx→(2+){x}sin(x−2)(x−2)2= (where [.] denotes the fractional part function) a. 0 b. 2 c. 1 d. does not exist
View Solutionlimx→1(x−1){x}. where {.) denotes the fractional part, is equal to:
View SolutionThe value of limx→0(tan({x}−1))sin{x}{x}({x}−1) is where {x} denotes the fractional part function
View Solutionlimx→0{(1+x)2x} (where {.} denotes the fractional part of x) is equal to
View Solution
