Let then :
i) Δ
depends on a
ii)Δ
depends on d
iii)Δ
is independent of a,d
iv)Δ
=
0
depends on a
depends on d
is independent of a,d
The correct Answer is:A, B
To solve the determinant Δ=∣∣
∣∣aa+da+3da+da+2daa+2daa+d∣∣
∣∣, we will follow these steps:
Step 1: Write the determinant
We start with the determinant as given:
Δ=∣∣
∣∣aa+da+3da+da+2daa+2daa+d∣∣
∣∣
Step 2: Simplify the determinant
We can perform row operations to simplify the determinant. Let's subtract the first row from the second and the third rows:
Δ=∣∣
∣
∣∣aa+da+3d(a+d−a)(a+2d−(a+d))(a−(a+3d))(a+2d−a)(a−(a+d))(a+d−(a+3d))∣∣
∣
∣∣
This simplifies to:
Δ=∣∣
∣∣aa+da+3ddd−3d2d−d−2d∣∣
∣∣
Step 3: Factor out common terms
Next, we can factor out d from the second and third rows:
Δ=d⋅d⋅∣∣
∣∣aa+da+3d11−32−1−2∣∣
∣∣
This gives us:
Δ=d2∣∣
∣∣aa+da+3d11−32−1−2∣∣
∣∣
Step 4: Calculate the determinant
Now we can calculate the determinant:
Δ=d2⋅(a∣∣∣1−3−1−2∣∣∣−(a+d)∣∣∣1−32−2∣∣∣+(a+3d)∣∣∣112−1∣∣∣)
Calculating the 2x2 determinants:
1. ∣∣∣1−3−1−2∣∣∣=(1)(−2)−(−3)(−1)=−2−3=−5
2. ∣∣∣1−32−2∣∣∣=(1)(−2)−(−3)(2)=−2+6=4
3. ∣∣∣112−1∣∣∣=(1)(−1)−(1)(2)=−1−2=−3
Putting it all together:
Δ=d2(a(−5)−(a+d)(4)+(a+3d)(−3))
Expanding this:
Δ=d2(−5a−4a−4d−3a−9d)=d2(−12a−13d)
Step 5: Conclusion
Thus, we have:
Δ=−d2(12a+13d)
Final Result
From this expression, we can conclude:
- Δ depends on d and a.
- Δ is not independent of a and d.
- Δ is not equal to zero unless both d and a are zero.
∣∣aa+da+3da+da+2daa+2daa+d∣∣
∣∣, we will follow these steps:
We start with the determinant as given:
Δ=∣∣
∣∣aa+da+3da+da+2daa+2daa+d∣∣
∣∣
We can perform row operations to simplify the determinant. Let's subtract the first row from the second and the third rows:
Δ=∣∣
∣
∣∣aa+da+3d(a+d−a)(a+2d−(a+d))(a−(a+3d))(a+2d−a)(a−(a+d))(a+d−(a+3d))∣∣
∣
∣∣
This simplifies to:
Δ=∣∣
∣∣aa+da+3ddd−3d2d−d−2d∣∣
∣∣
Next, we can factor out d from the second and third rows:
Δ=d⋅d⋅∣∣
∣∣aa+da+3d11−32−1−2∣∣
∣∣
This gives us:
Δ=d2∣∣
∣∣aa+da+3d11−32−1−2∣∣
∣∣
Now we can calculate the determinant:
Δ=d2⋅(a∣∣∣1−3−1−2∣∣∣−(a+d)∣∣∣1−32−2∣∣∣+(a+3d)∣∣∣112−1∣∣∣)
1. ∣∣∣1−3−1−2∣∣∣=(1)(−2)−(−3)(−1)=−2−3=−5
2. ∣∣∣1−32−2∣∣∣=(1)(−2)−(−3)(2)=−2+6=4
3. ∣∣∣112−1∣∣∣=(1)(−1)−(1)(2)=−1−2=−3
Δ=d2(a(−5)−(a+d)(4)+(a+3d)(−3))
Expanding this:
Δ=d2(−5a−4a−4d−3a−9d)=d2(−12a−13d)
Thus, we have:
Δ=−d2(12a+13d)
From this expression, we can conclude:
- Δ depends on d and a.
- Δ is not independent of a and d.
- Δ is not equal to zero unless both d and a are zero.
Topper's Solved these Questions
- DETERMINANTSBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - DETERMINANTSEXERCISE - EXERCISE-3:COMPREHENSION TYPE PROBLEMS
3 Videos
- DETERMINANTSBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - DETERMINANTSEXERCISE - EXERCISE-4 : SUBJECTIVE TYPE PROBLEMS
12 Videos
- DETERMINANTSBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - DETERMINANTSEXERCISE - EXERCISE-4 : SUBJECTIVE TYPE PROBLEMS
12 Videos
- CONTINUITY, DIFFERENTIABILITY AND DIFFERENTIATIONBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - CONTINUITY, DIFFERENTIABILITY AND DIFFERENTIATIONEXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
24 Videos
- DIFFERENTIAL EQUATIONSBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
6 Videos
Similar Questions
Knowledge Check
If c−3d4=d2, what is the ratio of c to d?
A5:1B3:2C4:3D3:4If A,B,C,D are angles of a quadrilateral, then sin A + sin (B+ C + D) = (i) 0 (ii) 1 (iii) 2 (iv) None of these
A0B1C2DNone of these
If c and d are integers, is c−3d even?
(1) c and d are odd.
(2) c−2d is odd.
View SolutionHow many integers are between? (i) −4 and 3 (ii) 5 and 12 (iii) −9 and−2 (iv) 0 and 5
View SolutionIf A=⎡⎢⎣3−342−340−11⎤⎥⎦ , then a. adj(adjA)=A b. |adj(adjA)|=1 c. adjA=I d. none of these
View SolutionLet A={a,b,{c,d}, e} . Which of the following statements are false and why? (i) {c,d}⊂A (ii) {c,d}∈A (iii) {{c,d}}⊂A
View Solution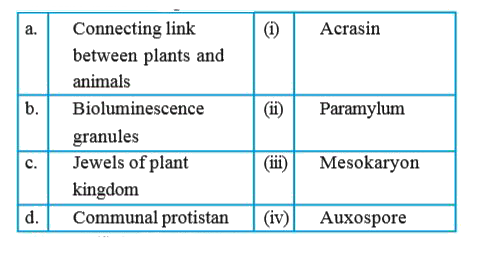
1 a(iii), b(ii), c(i), d(iv)
2 a(i), b(iv), c(i), d(iii)
3 a(iv), b(i), c(iii), d(iv)
4 a(ii), b(iii), c(iv), d(i)
View SolutionThe sum of the series a−(a+d)+(a+2d)−(a+3d)+... up to (2n+1) terms is: a. −nd. b. a+2nd. c. a+nd. d. 2nd
View Solution
