Which of the following graph represent the function du, for
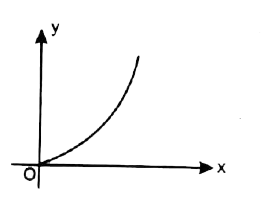
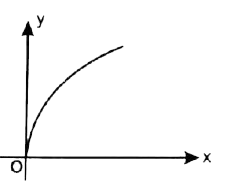
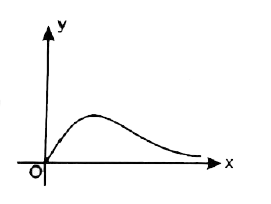
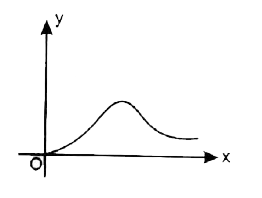
The correct Answer is:B
To solve the problem, we need to analyze the function given by the integral:
f(x)=∫√x0eu2xdu
for x>0 and f(0)=0.
Step 1: Applying the Fundamental Theorem of Calculus
We will differentiate f(x) with respect to x using the Leibniz rule (also known as the Fundamental Theorem of Calculus). According to this theorem:
ddx(∫b(x)a(x)f(u,x)du)=f(b(x),x)⋅b′(x)−f(a(x),x)⋅a′(x)+∫b(x)a(x)∂f∂xdu
In our case, a(x)=0, b(x)=√x, and f(u,x)=eu2x.
Step 2: Finding f(b(x),x) and b′(x)
1. Evaluate f(b(x),x):
f(b(x),x)=e(√x)2x=exx=e1=e
2. Find b′(x):
b′(x)=ddx(√x)=12√x
Step 3: Finding f(a(x),x) and a′(x)
1. Evaluate f(a(x),x):
f(a(x),x)=f(0,x)=e02x=e0=1
2. Find a′(x):
a′(x)=0
Step 4: Finding ∂f∂x
Now we need to find ∂f∂x:
∂∂x(eu2x)=eu2x⋅(−u2x2)
Step 5: Putting it all together
Now we can apply the Leibniz rule:
f′(x)=e⋅12√x−0+∫√x0eu2x(−u2x2)du
Step 6: Analyzing the behavior of f(x)
1. As x→0, f(0)=0 is given.
2. For x>0, f(x) is positive and increases as x increases.
Step 7: Finding the graph representation
From our analysis, we can see that the function behaves like a parabola. Since f(0)=0 and increases for x>0, we can represent it as:
y^2 = e^2 x \quad \text{(where e^2 is a constant)}
This is a standard form of a parabola opening to the right.
Conclusion
The graph of the function f(x) is a parabola that opens to the right, which corresponds to the equation y2=4ax where a=e24.
f(b(x),x)=e(√x)2x=exx=e1=e
b′(x)=ddx(√x)=12√x
f(a(x),x)=f(0,x)=e02x=e0=1
a′(x)=0
∂∂x(eu2x)=eu2x⋅(−u2x2)
f′(x)=e⋅12√x−0+∫√x0eu2x(−u2x2)du
2. For x>0, f(x) is positive and increases as x increases.
y^2 = e^2 x \quad \text{(where e^2 is a constant)}
Topper's Solved these Questions
- APPLICATION OF DERIVATIVES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (ONE OR MORE THAN ANSWER IS/ARE CORRECT )
29 Videos
- APPLICATION OF DERIVATIVES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)
15 Videos
- AREA UNDER CURVESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - AREA UNDER CURVESEXERCISE - AXERCISE (SUBJECTIVE TYPE PROBLEMS)
8 Videos
Similar Questions
Knowledge Check
The least value of the function f(x)=ax+bx(x>0,a>0,b>0)
A√abB2√abCabD2ab
For the functions f(x)=∫x0sinttdt where x>0. At x=nπ f(x) attains
View SolutionIf the function f(x)=x(esinx−1)1−cosx is continuous at x =0 then f(0)=
View SolutionLet f(x) be a differentiable function satisfying f(x)=∫x0e(2tx−t2)cos(x−t)dt, then find the value of f''(0).
View SolutionIf the function f(x)={3x<012x>0 then limx→0f(x)=
View SolutionLet f be a differentiable function such that f'(x)=f(x)+∫20f(x)dxandf(0)=4−e23. Find f(x).
View SolutionIf F(x)=∫x3x2logtdt(x>0), then F'(x) equals
View SolutionEquation of normal drawn to the graph of the function defined as f(x) = sinx2x , x≠0 and f(0) =0, at the origin.
View Solution
