The rule of an "obstacle course" specifies that at the nth obstacle a person has to tos a fair 6 sided die n times. If the sum of points in these n tosses is bigger than 2n, the person is said to have crossed the obstacle.
Q. The probability that a person crosses the first three obstacles :
143216
100243
216243
100216
The correct Answer is:B
To solve the problem of finding the probability that a person crosses the first three obstacles in the obstacle course, we will follow these steps:
Step 1: Calculate Probability for the First Obstacle (n = 1)
At the first obstacle, the person rolls a die once (n = 1). The condition to cross the obstacle is that the sum of the points must be greater than 21=2.
- Total Outcomes: The possible outcomes when rolling a die once are {1, 2, 3, 4, 5, 6}. Thus, there are 6 total outcomes.
- Favorable Outcomes: The outcomes that are greater than 2 are {3, 4, 5, 6}. Hence, there are 4 favorable outcomes.
Probability (P1):
P1=Number of favorable outcomesTotal outcomes=46=23
Step 2: Calculate Probability for the Second Obstacle (n = 2)
At the second obstacle, the person rolls the die twice (n = 2). The condition to cross this obstacle is that the sum of the points must be greater than 22=4.
- Total Outcomes: The total outcomes when rolling a die twice are 6×6=36.
- Favorable Outcomes: We need to find pairs (x, y) such that x+y>4. The pairs that satisfy this condition are:
- For (1, _): (1, 4), (1, 5), (1, 6) → 3 outcomes
- For (2, _): (2, 3), (2, 4), (2, 5), (2, 6) → 4 outcomes
- For (3, _): (3, 2), (3, 3), (3, 4), (3, 5), (3, 6) → 5 outcomes
- For (4, _): (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6) → 6 outcomes
- For (5, _): (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6) → 6 outcomes
- For (6, _): (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) → 6 outcomes
Counting these gives us:
- 3 + 4 + 5 + 6 + 6 + 6 = 30 favorable outcomes.
Probability (P2):
P2=3036=56
Step 3: Calculate Probability for the Third Obstacle (n = 3)
At the third obstacle, the person rolls the die three times (n = 3). The condition to cross this obstacle is that the sum of the points must be greater than 23=8.
- Total Outcomes: The total outcomes when rolling a die three times are 63=216.
- Favorable Outcomes: We need to find combinations (x, y, z) such that x+y+z>8. The total combinations can be calculated by finding the total combinations that yield sums of 3 to 8 and subtracting them from 216.
Calculating the sums:
- The minimum sum (1+1+1) = 3.
- The maximum sum (6+6+6) = 18.
The combinations yielding sums ≤ 8 can be calculated systematically or through generating functions, but for simplicity, we can use the complementary counting approach.
After calculating or using a generating function, we find that the number of outcomes where x+y+z≤8 is 56.
Thus, the favorable outcomes for crossing the third obstacle are:
216−56=160
Probability (P3):
P3=160216=2027
Step 4: Calculate the Overall Probability
The overall probability that the person crosses all three obstacles is the product of the individual probabilities:
P=P1×P2×P3=23×56×2027
Calculating this gives:
P=2×5×203×6×27=200486=100243
Final Answer
The probability that a person crosses the first three obstacles is 100243.
---
At the first obstacle, the person rolls a die once (n = 1). The condition to cross the obstacle is that the sum of the points must be greater than 21=2.
- Favorable Outcomes: The outcomes that are greater than 2 are {3, 4, 5, 6}. Hence, there are 4 favorable outcomes.
P1=Number of favorable outcomesTotal outcomes=46=23
At the second obstacle, the person rolls the die twice (n = 2). The condition to cross this obstacle is that the sum of the points must be greater than 22=4.
- Favorable Outcomes: We need to find pairs (x, y) such that x+y>4. The pairs that satisfy this condition are:
- For (1, _): (1, 4), (1, 5), (1, 6) → 3 outcomes
- For (2, _): (2, 3), (2, 4), (2, 5), (2, 6) → 4 outcomes
- For (3, _): (3, 2), (3, 3), (3, 4), (3, 5), (3, 6) → 5 outcomes
- For (4, _): (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6) → 6 outcomes
- For (5, _): (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6) → 6 outcomes
- For (6, _): (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) → 6 outcomes
- 3 + 4 + 5 + 6 + 6 + 6 = 30 favorable outcomes.
P2=3036=56
At the third obstacle, the person rolls the die three times (n = 3). The condition to cross this obstacle is that the sum of the points must be greater than 23=8.
- Favorable Outcomes: We need to find combinations (x, y, z) such that x+y+z>8. The total combinations can be calculated by finding the total combinations that yield sums of 3 to 8 and subtracting them from 216.
- The minimum sum (1+1+1) = 3.
- The maximum sum (6+6+6) = 18.
216−56=160
P3=160216=2027
The overall probability that the person crosses all three obstacles is the product of the individual probabilities:
P=P1×P2×P3=23×56×2027
P=2×5×203×6×27=200486=100243
The probability that a person crosses the first three obstacles is 100243.
Topper's Solved these Questions
- PROBABILITY BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - PROBABILITY EXERCISE - Exercise-4 : Matching Type Problems
1 Video
- PROBABILITY BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - PROBABILITY EXERCISE - Exercise -5 : Subjective Type problems
11 Videos
- PROBABILITY BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - PROBABILITY EXERCISE - Exercise-2 : One or More than One Answer is/are Correct
4 Videos
- PERMUTATION AND COMBINATIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - PERMUTATION AND COMBINATIONS EXERCISE - Exercise-5 : Subjective Type Problems
13 Videos
- QUADRATIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
45 Videos
Similar Questions
The rule of an "obstacle course" specifies that at the nth obstacle a person has to tos a fair 6 sided die n times. If the sum of points in these n tosses is bigger than 2n, the person is said to have crossed the obstacle.
Q. The probability that a person crosses the first two obstacles but fails to cross the third obstacle.
View SolutionA fair coin is tossed 2n times, The probability of getting as many heads in the first n tosses as in the last n is
View SolutionA bag contains (2n+1) coins. It is known that n of these coins have a head on both sides whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is 3142 , determine the value of n .
View SolutionA bag contains (2n+1) coins. It is known that n of these coins have a head on both sides whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is 3142 , determine the value of n .
View SolutionA box contains N coins, m of which are fair and the rest are biased. The probability of getting a head when a fair coin is tossed is 1/2 while it is 2/3 when a biased coin is tossed. A coin is drawn from the box at random and is tossed twice. The first time it shows head and the second time it shows tail. What is the probability that the coin drawn is fair?
View SolutionDie A has 4 red and 2 white faces, whereas die B has 2 red and 4 white faces. A coins is flipped once. If it shows a head, the game continues by throwing die A: if it shows tail, then die B is to be used. If the probability that die A is used is 32/33 when it is given that red turns up every time in first n throws, then find the value of n.
View SolutionDie A has 4 red and 2 white faces, whereas die B has 2 red and 4 white faces. A coins is flipped once. If it shows a head, the game continues by throwing die A: if it shows tail, then die B is to be used. If the probability that die A is used is 32/33 when it is given that red turns up every time in first n throws, then find the value of n.
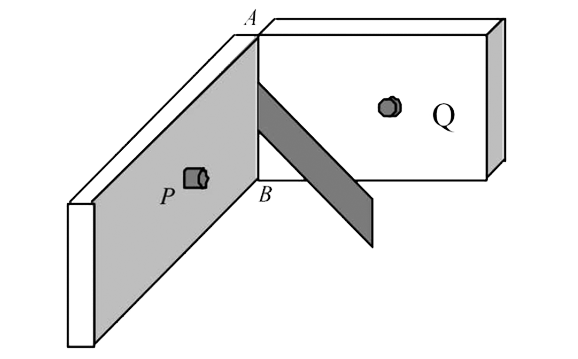
View SolutionTwo heavy metallic plates are joined together at 90∘ to each other. A laminar sheet of mass 30kg is hinged at the line AB joining the two heavy metallic plates. The hinges are frictionless. The moment of inertia of the laminar sheet about an axis parallel to AB and passing through its center of mass is 1.2 kg m2. Two rubber obstacles P and Q are fixed, one on each metallic plate at a distance 0.5m from the line AB. This distance is chosen so that the reaction due to the hinges on the laminar sheet is zero during the impact. Initially the laminar sheet hits one of the obstacles with an angular velocity 1 rad/s and turns back. If the impulse on the sheet due to each obstacal is 6 N-s,
(a) Find the location of the center of mass of the laminar sheet from AB.
(b) At what angular velocity does the laminar sheet come back after the first impact?
(c) After how many impacts, does the laminar sheet come to rest?
View SolutionIf N is the number of ways in which a person can walk up a stairway which has 7 steps if he can take 1 or 2 steps up the stairs at a time then the value of N/3 is _______.
View SolutionTwo person pull a rope towards themselves. Each person exerts a force of 100 N on the rope. Find the Young modulus of the material of the rope if it extends in length by 1 cm. Original length of the rope=2 m and the area of cross section =2cm2.
View Solution
