The graph of x4=x2y2 is a union of n different lines, then the value of n is.
The correct Answer is:3
To solve the equation x4=x2y2 and determine the number of different lines represented by the graph, we can follow these steps:
Step 1: Rearrange the equation
Start with the given equation:
x4=x2y2
We can rearrange this by bringing all terms to one side:
x4−x2y2=0
Step 2: Factor the equation
Next, we can factor out x2 from the equation:
x2(x2−y2)=0
Step 3: Set each factor to zero
Now, we set each factor equal to zero:
1. x2=0
2. x2−y2=0
Step 4: Solve the first equation
From the first equation x2=0:
x=0
This represents a vertical line along the y-axis.
Step 5: Solve the second equation
From the second equation x2−y2=0:
y2=x2
Taking the square root of both sides gives us:
y=xandy=−x
These represent two lines: one with a positive slope (y = x) and one with a negative slope (y = -x).
Step 6: Count the lines
Now, we have identified:
1. One line from x=0 (the y-axis).
2. Two lines from y=x and y=−x.
In total, we have:
1+2=3 lines
Conclusion
Thus, the value of n, which represents the number of different lines in the graph, is:
3
---
Start with the given equation:
x4=x2y2
We can rearrange this by bringing all terms to one side:
x4−x2y2=0
Next, we can factor out x2 from the equation:
x2(x2−y2)=0
Now, we set each factor equal to zero:
1. x2=0
2. x2−y2=0
From the first equation x2=0:
x=0
This represents a vertical line along the y-axis.
From the second equation x2−y2=0:
y2=x2
Taking the square root of both sides gives us:
y=xandy=−x
These represent two lines: one with a positive slope (y = x) and one with a negative slope (y = -x).
Now, we have identified:
1. One line from x=0 (the y-axis).
2. Two lines from y=x and y=−x.
1+2=3 lines
Thus, the value of n, which represents the number of different lines in the graph, is:
3
Topper's Solved these Questions
- STRAIGHT LINES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-4 : Matching Type Problems
2 Videos
- SOLUTION OF TRIANGLESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-5 : Subjective Type Problems
11 Videos
- TRIGONOMETRIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems
9 Videos
Similar Questions
Knowledge Check
If 4x⋅n2=4x+1⋅n and x and n are both positive integers, what is the value of n?
A2B4C6D8
If the line passing through (4,3)and(2,k) is parallel to the line y=2x+3, then find the value of k.
View SolutionIf the line passing through (4,3)and(2,k) is parallel to the line y=2x+3, then find the value of k.
View Solution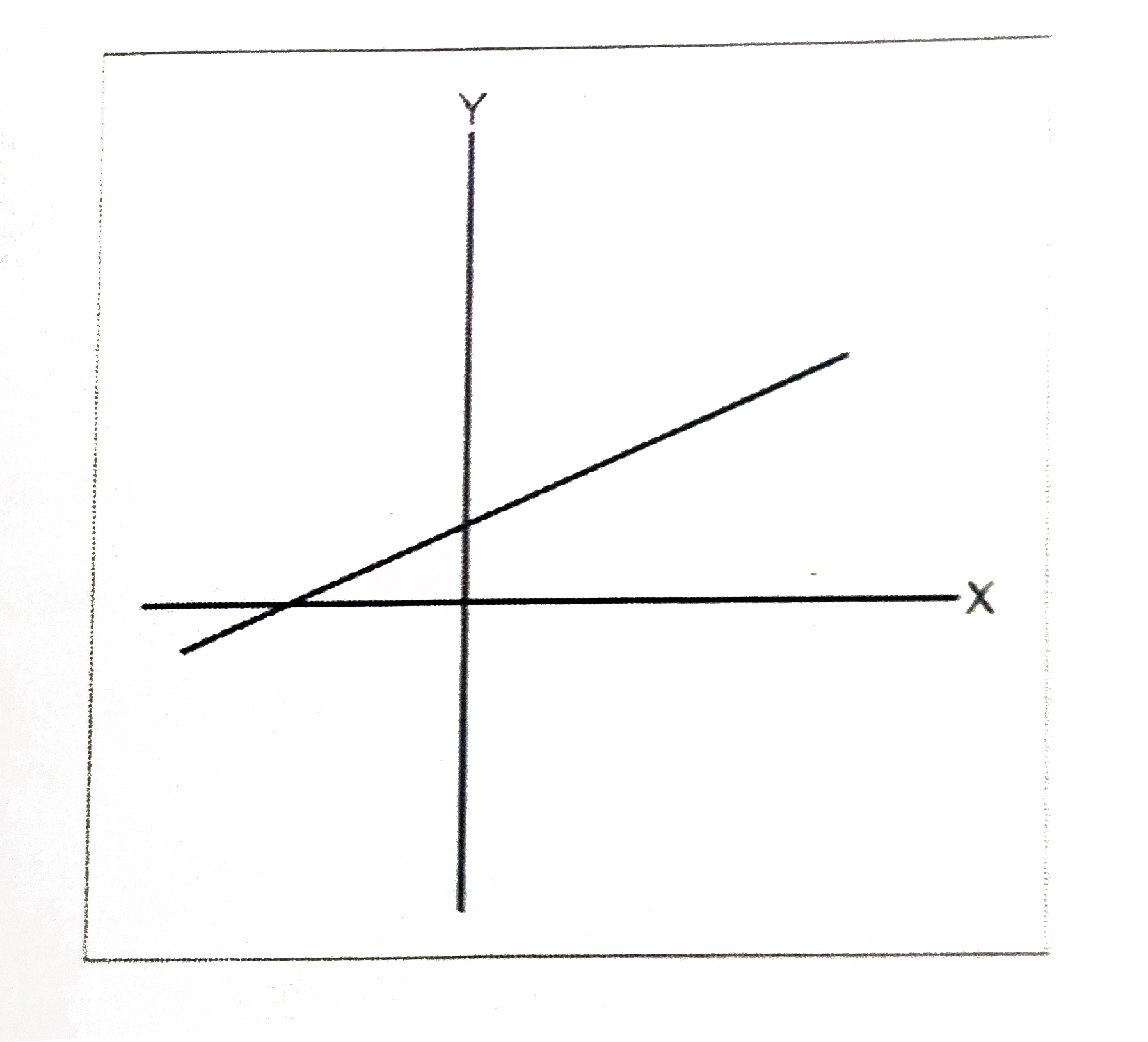
The graph below depicts the straight line y=x2+3. If the line is reflected about the X axis and the equation of the new lines is y=mx+n, what is the value of |m+n| ?
View SolutionDraw the graph of the equation x+2y =4, use graph to find :
(a) X1, the value of x when y=4(b)Y1 the value of y when x= -2
View SolutionIf the line lx+my+n=0 cuts the ellipse (x2a2)+(y2b2)=1 at points whose eccentric angles differ by π2, then find the value of a2l2+b2m2n2 .
View SolutionIf x∈[(4n+1)π2,(4n+3)π2] and n∈N, then the value of ∫x0[cost]dt, is
View SolutionThe 2nd, 3rd and 4th terms in the expansion of (x+y)n are 240,720and1080 respectively, find the values of x,yandn.
View Solution
