Points AandB lie on the parabola y=2x2+4x−2, such that origin is the mid-point of the linesegment AB. If l be the length of the line segment AB, then find the unit digit of l2.
The correct Answer is:8
To solve the problem step by step, we will follow the reasoning outlined in the video transcript while providing a clearer structure.
Step 1: Identify the Parabola
The equation of the parabola is given as:
y=2x2+4x−2
Step 2: Find the Vertex of the Parabola
To rewrite the parabola in vertex form, we can complete the square:
1. Factor out the coefficient of x2:
y=2(x2+2x)−2
2. Complete the square inside the parentheses:
y=2((x+1)2−1)−2
y=2(x+1)2−2−2
y=2(x+1)2−4
The vertex of the parabola is at the point (−1,−4).
Step 3: Determine the Points A and B
Given that the origin (0, 0) is the midpoint of the line segment AB, we can denote the coordinates of points A and B as:
- A(x1,y1)
- B(x2,y2)
Since the midpoint is at the origin:
x1+x22=0⇒x1+x2=0
This implies x2=−x1.
Step 4: Find the Equation of Line AB
The line segment AB can be represented as:
y=mx
Since it passes through the origin.
Step 5: Find the Intersection of Line AB with the Parabola
Substituting y=mx into the parabola's equation:
mx=2x2+4x−2
Rearranging gives:
2x2+(4−m)x−2=0
Step 6: Use the Condition for the Midpoint
From the quadratic equation, the sum of the roots x1+x2 can be expressed as:
x1+x2=−ba=−4−m2
Setting this equal to zero (from the midpoint condition):
−4−m2=0
This leads to:
4−m=0⇒m=4
Step 7: Substitute m Back into the Line Equation
Now we have the equation of line AB:
y=4x
Step 8: Find the Points of Intersection
Substituting y=4x back into the parabola:
4x=2x2+4x−2
This simplifies to:
2x2−2=0
x2=1⇒x=1 or x=−1
Step 9: Calculate the Corresponding y-coordinates
For x=1:
y=4(1)=4⇒A(1,4)
For x=−1:
y=4(−1)=−4⇒B(−1,−4)
Step 10: Calculate the Length of Segment AB
The length l of segment AB is given by the distance formula:
l=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of A and B:
l=√((−1)−1)2+((−4)−4)2=√(−2)2+(−8)2=√4+64=√68
Step 11: Find l2 and its Unit Digit
Calculating l2:
l2=68
The unit digit of l2 is 8.
Final Answer
The unit digit of l2 is 8.
The equation of the parabola is given as:
y=2x2+4x−2
To rewrite the parabola in vertex form, we can complete the square:
1. Factor out the coefficient of x2:
y=2(x2+2x)−2
2. Complete the square inside the parentheses:
y=2((x+1)2−1)−2
y=2(x+1)2−2−2
y=2(x+1)2−4
Given that the origin (0, 0) is the midpoint of the line segment AB, we can denote the coordinates of points A and B as:
- A(x1,y1)
- B(x2,y2)
x1+x22=0⇒x1+x2=0
This implies x2=−x1.
The line segment AB can be represented as:
y=mx
Since it passes through the origin.
Substituting y=mx into the parabola's equation:
mx=2x2+4x−2
Rearranging gives:
2x2+(4−m)x−2=0
From the quadratic equation, the sum of the roots x1+x2 can be expressed as:
x1+x2=−ba=−4−m2
Setting this equal to zero (from the midpoint condition):
−4−m2=0
This leads to:
4−m=0⇒m=4
Now we have the equation of line AB:
y=4x
Substituting y=4x back into the parabola:
4x=2x2+4x−2
This simplifies to:
2x2−2=0
x2=1⇒x=1 or x=−1
For x=1:
y=4(1)=4⇒A(1,4)
For x=−1:
y=4(−1)=−4⇒B(−1,−4)
The length l of segment AB is given by the distance formula:
l=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of A and B:
l=√((−1)−1)2+((−4)−4)2=√(−2)2+(−8)2=√4+64=√68
Calculating l2:
l2=68
The unit digit of l2 is 8.
The unit digit of l2 is 8.
Topper's Solved these Questions
- PARABOLABOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - PARABOLAEXERCISE - Exercise-4 : Matching Type Problems
2 Videos
- MATRICES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - MATRICES EXERCISE - Exercise-4 : Subjective Type Problems
4 Videos
- PERMUTATION AND COMBINATIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - PERMUTATION AND COMBINATIONS EXERCISE - Exercise-5 : Subjective Type Problems
13 Videos
Similar Questions
If P is a point on the parabola y2=8x and A is the point (1,0) then the locus of the mid point of the line segment AP is
View SolutionThe points A(3, 6) and B lie on the parabola y2=4ax, such that the chord AB subtends 90∘ at the origin, then the length of the chord AB is equal to
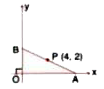
View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
View SolutionIf P(2, 6) is the mid-point of the line segment joining A(6, 5) and B(4, y) , find y .
View Solutiony=3x is tangent to the parabola 2y=ax2+ab.
If b=36,then the point of contact is
View SolutionFind the position vector of the mid point of the line segment AB, where A is the point (3, 4, -2) and B is the point (1, ,2 4).
View SolutionIf P(x, 6) is the mid-point of the line segment joining A(6, 5) and B(4, y) , find y .
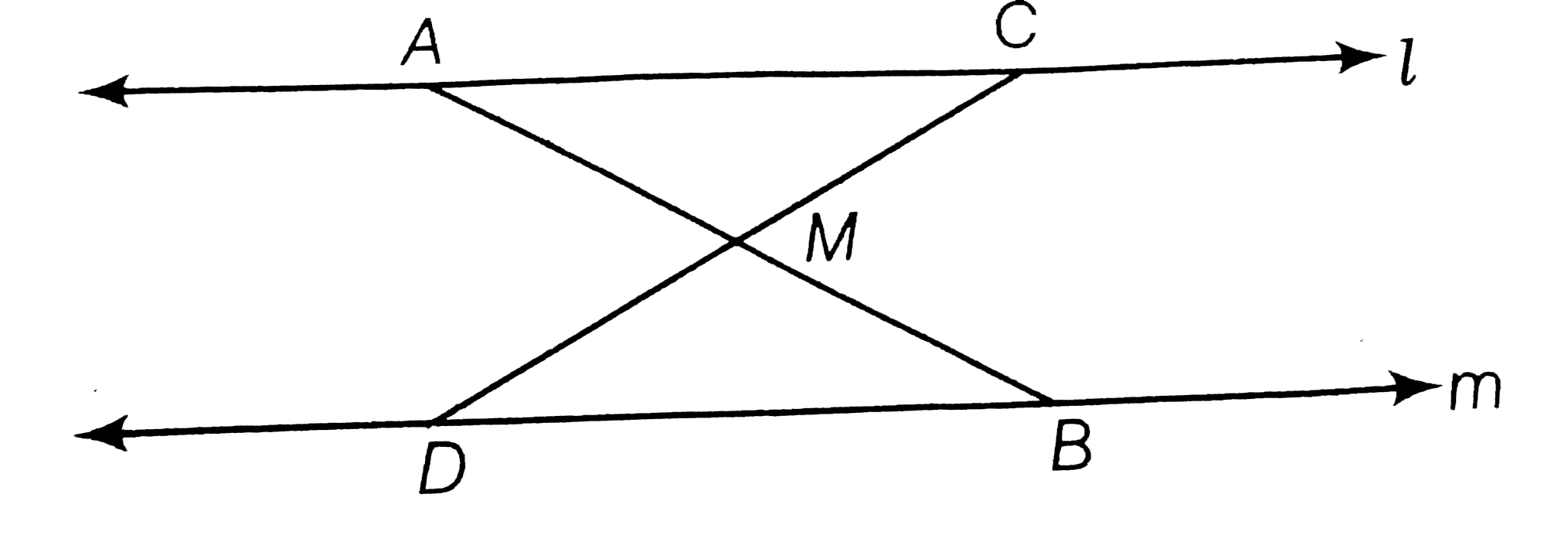
View SolutionIn the given figure l||m and M is the mid-point of a line segment AB .Show that M is also the mid- point of any line segment CD, having its end points on l and m, respectively.
View Solutionif the line 4x+3y+1=0 meets the parabola y2=8x then the mid point of the chord is
View SolutionFind the distance of the point (1, 2) from the mid-point of the line segment joining the points (6, 8) and (2, 4) .
View Solution
