Identify the correct options :
sin3αcos2α>0 for α∈(3π8,23π48)
sin3αcos2α<0 for α∈(13π48,14π48)
sin2αcosα<0 for α∈(−π2,0)
sin2αcosα>0 for α∈(13π48,14π48)
The correct Answer is:A, B, C, D
To solve the problem, we need to analyze the expression sin3αcos2α and determine the conditions under which it is greater than zero.
1. Understanding the Expression:
We start with the expression:
sin3αcos2α>0
This implies that both sin3α and cos2α must either be both positive or both negative.
2. Finding Conditions for sin3α>0:
The sine function is positive in the intervals:
3α∈(0,π)∪(2π,3π)∪(4π,5π)…
This translates to:
α∈(0,π3)∪(2π3,π)∪(4π3,5π3)…
3. Finding Conditions for cos2α>0:
The cosine function is positive in the intervals:
2α∈(−π2,π2)∪(3π2,5π2)…
This translates to:
α∈(−π4,π4)∪(3π4,5π4)…
4. Combining the Conditions:
We need to find the intersection of the intervals where both conditions hold true:
- From sin3α>0: α∈(0,π3) or (2π3,π)
- From cos2α>0: α∈(−π4,π4) or (3π4,5π4)
The only overlapping interval is:
α∈(0,π4)
5. Analyzing the Negative Cases:
Now we consider when both sin3α<0 and cos2α<0:
- sin3α<0 gives us intervals like (π3,π) and so on.
- cos2α<0 gives us intervals like (π4,3π4).
The overlapping interval here is:
α∈(π3,3π4)
6. Final Intervals:
Thus, the complete solution for sin3αcos2α>0 is:
α∈(0,π4)∪(π3,3π4)
Conclusion:
Based on the intervals derived, we can now check the provided options to identify which ones fall within these ranges.
We start with the expression:
sin3αcos2α>0
This implies that both sin3α and cos2α must either be both positive or both negative.
The sine function is positive in the intervals:
3α∈(0,π)∪(2π,3π)∪(4π,5π)…
This translates to:
α∈(0,π3)∪(2π3,π)∪(4π3,5π3)…
The cosine function is positive in the intervals:
2α∈(−π2,π2)∪(3π2,5π2)…
This translates to:
α∈(−π4,π4)∪(3π4,5π4)…
We need to find the intersection of the intervals where both conditions hold true:
- From sin3α>0: α∈(0,π3) or (2π3,π)
- From cos2α>0: α∈(−π4,π4) or (3π4,5π4)
α∈(0,π4)
Now we consider when both sin3α<0 and cos2α<0:
- sin3α<0 gives us intervals like (π3,π) and so on.
- cos2α<0 gives us intervals like (π4,3π4).
α∈(π3,3π4)
Thus, the complete solution for sin3αcos2α>0 is:
α∈(0,π4)∪(π3,3π4)
Based on the intervals derived, we can now check the provided options to identify which ones fall within these ranges.
Topper's Solved these Questions
- TRIGONOMETRIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-3 : Comprehension Type Problems
3 Videos
- TRIGONOMETRIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-4 : Matching Type Problems
2 Videos
- TRIGONOMETRIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems
9 Videos
- STRAIGHT LINES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-5 : Subjective Type Problems
10 Videos
- VECTOR & 3DIMENSIONAL GEOMETRYBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-5 : Subjective Type Problems
16 Videos
Similar Questions
Knowledge Check
Match the column:
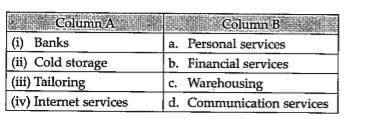
Identify the correct option:A1-a, 2-0, 3-6, 4-dB1-6, 2-c, 3-a, 4-dC1-b, 2-c, 3-d, 4-aD1-a, 2-b, 3-c, 4-d
Identify the correct option regarding the structure given below .

View SolutionIdentify the correct option in column I, II and III

View Solution[r]= concentration of reactant and t be the time
_2019_CBT3_E01_012_Q01.png)
Identify the correct option for order-
View SolutionIdentify the correct option for the order of specific charge of the
given particles.
View SolutionWhat is the role of gypsum, CaSo4.2H2O in setting of cement? Identify the correct option from the following:
View SolutionIdentify the correct option:
Biological NameFamilyOrderClassMangifera indicaABCTriticum aestivumDEF
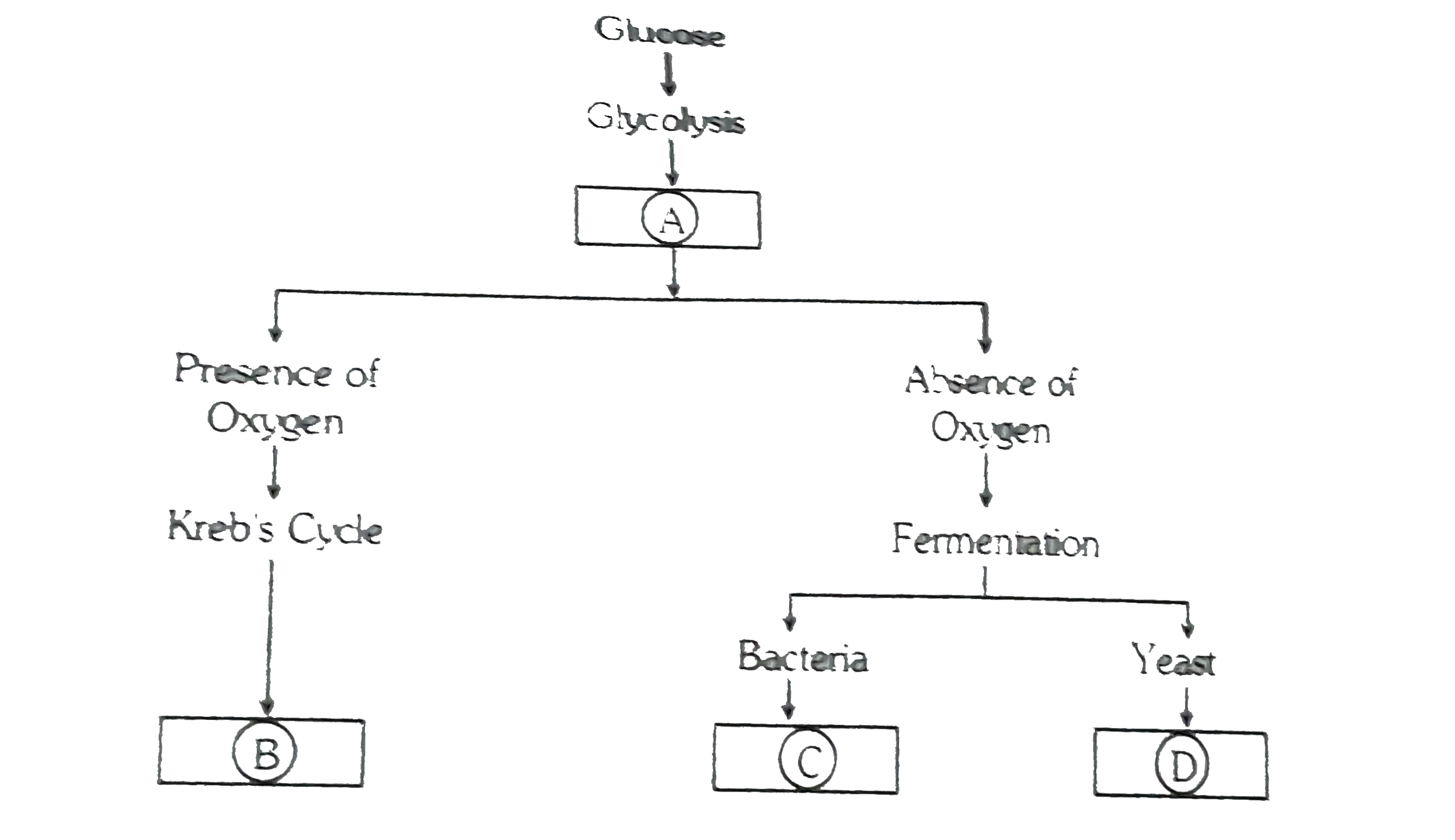
View SolutionThe following is a simplified scheme showing the fate of glucose during aerobic and annaerobic respiration. Identify the end products that are formed at stages indicated as A,B, C and D. Identify the correct option from those given below.
View Solution
