is an excentral triangle of an equilateral triangle such that unit, if is pedal triangle of , then
16
4
2
1
The correct Answer is:A
To solve the problem, we need to find the ratio of the areas of two triangles: the excentral triangle ΔI1I2I3 and the pedal triangle ΔDEF of the equilateral triangle ΔABC.
1. Understanding the Triangles:
- We have an equilateral triangle ΔABC.
- The excentral triangle ΔI1I2I3 has a side I1I2=4 units.
- The pedal triangle ΔDEF is formed by dropping perpendiculars from the vertices of ΔABC to the opposite sides.
2. Properties of the Excentral Triangle:
- Since ΔI1I2I3 is an equilateral triangle (as it is an excentral triangle of ΔABC), all sides are equal. Thus, I1I2=I2I3=I3I1=4 units.
3. Finding the Area of ΔI1I2I3:
- The area A of an equilateral triangle with side length s is given by the formula:
A=√34s2
- For ΔI1I2I3:
AI1I2I3=√34(42)=√34×16=4√3
4. Finding the Area of ΔDEF:
- The pedal triangle ΔDEF is also equilateral. The side length of ΔDEF can be determined from the properties of the pedal triangle in relation to ΔABC.
- Since ΔABC is equilateral and I1I2I3 is an excentral triangle, the side length of ΔDEF is half of that of ΔI1I2I3 because the pedal triangle is inscribed within the original triangle.
- Thus, the side length of ΔDEF is 1 unit.
- Now, we can find the area of ΔDEF:
ADEF=√34(12)=√34
5. Finding the Ratio of Areas:
- We need to find the ratio of the areas of ΔI1I2I3 to ΔDEF:
Ratio=AI1I2I3ADEF=4√3√34=4√3×4√3=16
Final Answer:
Ar(ΔI1I2I3)Ar(ΔDEF)=16
- We have an equilateral triangle ΔABC.
- The excentral triangle ΔI1I2I3 has a side I1I2=4 units.
- The pedal triangle ΔDEF is formed by dropping perpendiculars from the vertices of ΔABC to the opposite sides.
- Since ΔI1I2I3 is an equilateral triangle (as it is an excentral triangle of ΔABC), all sides are equal. Thus, I1I2=I2I3=I3I1=4 units.
- The area A of an equilateral triangle with side length s is given by the formula:
A=√34s2
- For ΔI1I2I3:
AI1I2I3=√34(42)=√34×16=4√3
- The pedal triangle ΔDEF is also equilateral. The side length of ΔDEF can be determined from the properties of the pedal triangle in relation to ΔABC.
- Since ΔABC is equilateral and I1I2I3 is an excentral triangle, the side length of ΔDEF is half of that of ΔI1I2I3 because the pedal triangle is inscribed within the original triangle.
- Thus, the side length of ΔDEF is 1 unit.
- Now, we can find the area of ΔDEF:
ADEF=√34(12)=√34
- We need to find the ratio of the areas of ΔI1I2I3 to ΔDEF:
Ratio=AI1I2I3ADEF=4√3√34=4√3×4√3=16
Ar(ΔI1I2I3)Ar(ΔDEF)=16
Topper's Solved these Questions
- SOLUTION OF TRIANGLESBook:VIKAS GUPTA (BLACK BOOK) ENGLISHChapter:SOLUTION OF TRIANGLESExercise:Exercise-2 : One or More than One Answer is/are Correct
Explore 15 Videos
- SOLUTION OF TRIANGLESBook:VIKAS GUPTA (BLACK BOOK) ENGLISHChapter:SOLUTION OF TRIANGLESExercise:Exercise-3 : Comprehension Type Problems
Explore 13 Videos
- SEQUENCE AND SERIES Book:VIKAS GUPTA (BLACK BOOK) ENGLISHChapter:SEQUENCE AND SERIES Exercise:EXERCISE (SUBJECTIVE TYPE PROBLEMS)
Explore 21 Videos
- STRAIGHT LINES Book:VIKAS GUPTA (BLACK BOOK) ENGLISHChapter:STRAIGHT LINES Exercise:Exercise-5 : Subjective Type Problems
Explore 10 Videos
Similar Questions
Knowledge Check
A current of 6 A enters one corner P of an equilateral triangle PQR having 3 wires of resistances 2 Q each and leaves by the corner R. Then the currents I1andI2 are
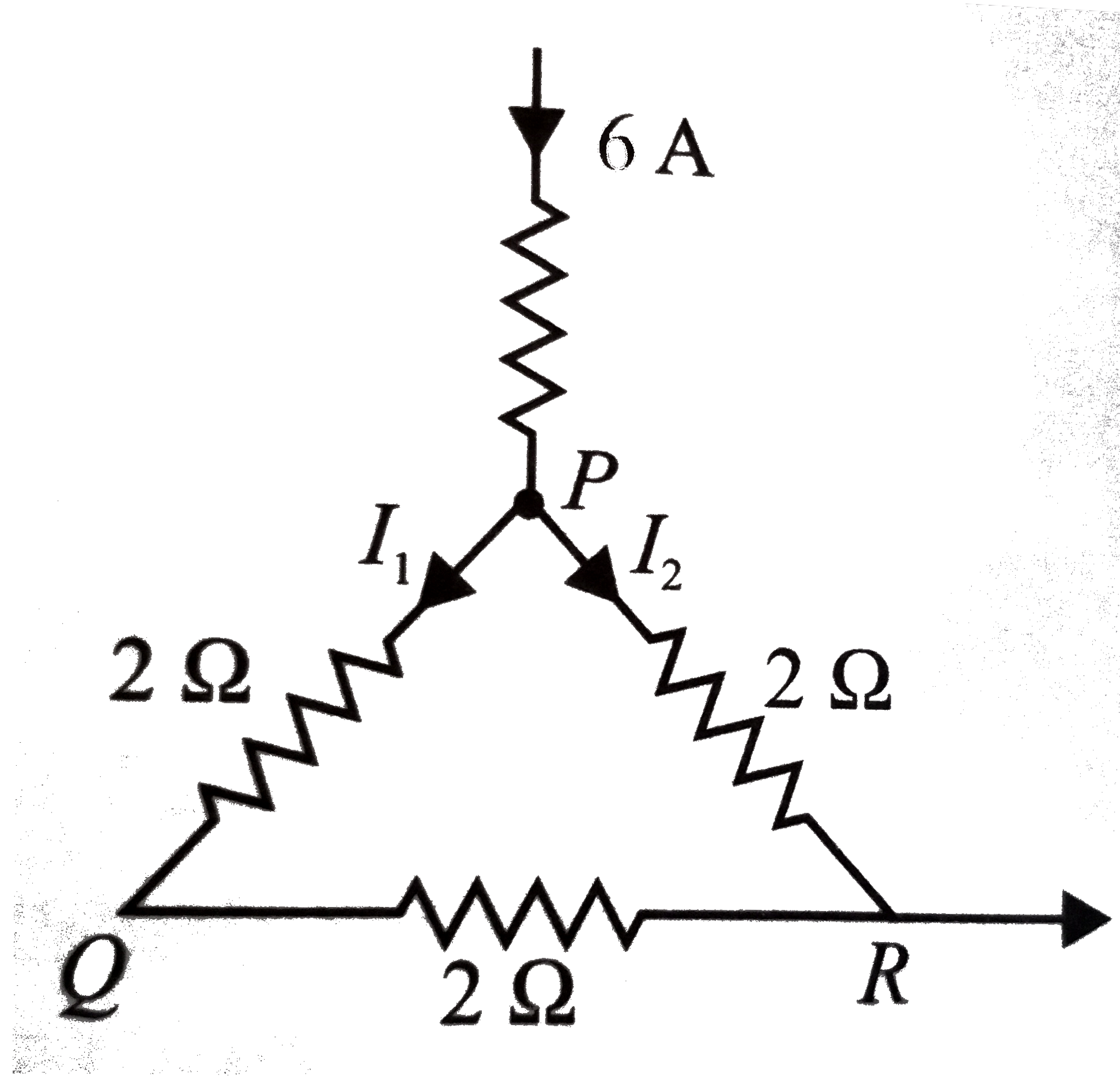 A2A,4AB4A,2AC1A,2AD2A,3A
A2A,4AB4A,2AC1A,2AD2A,3A
If z1,z2andz3, are the vertices of an equilateral triangle ABC such that |z1−i|=|z2−i|=|z3−i|.then |z1+z2+z3|equals:
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=14ar(ΔABC).
View Solutionz1,z2,z3 are the vertices of an equilateral triangle taken in counter clockwise direction. If its circumference is at the origin and z1=1+i, then
View SolutionIn a triangle ABC I1,I2,I3 are excentre of triangle then show that II1.II2.II3=16R2r.
View SolutionIf I1,I2,I3 are excentres of the triangle with vertices (0, 0), (5, 12), (16, 12) then the orthocentre of ΔI1I2I3 is
View SolutionIf I1,I2,I3 are the centers of escribed circles of triangle ABC, show that area of triangle I1I2I3=abc2r.
View Solutionz1,z2,z3 are the vertices of an equilateral triangle taken in counter clockwise direction. If its circumcenter is at (1−2i) and (z1=2+i), then z2=
View Solution