Let ABC be a triangle with ∠BAC=2π/3andAB=x such that (AB) (AC) = 1. If x varies, then find the longest possible length of the angle bisector AD
13
12
23
√23
The correct Answer is:B
Step by step video & image solution for Let ABC be a triangle with angleBAC = 2pi//3 and AB = x such that (AB) (AC) = 1. If x varies, then find the longest possible length of the angle bisector AD by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOLUTION OF TRIANGLESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-2 : One or More than One Answer is/are Correct
15 Videos
- SOLUTION OF TRIANGLESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-3 : Comprehension Type Problems
13 Videos
- SEQUENCE AND SERIES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
21 Videos
- STRAIGHT LINES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-5 : Subjective Type Problems
10 Videos
Similar Questions
ABC is a triangle right angled at C. If AB=25cmandAC=7cm, find BC.
View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If AD⊥BC, find the length of AD .
View SolutionletABC be a right angled triangle at C.If the inscribed circle touches the side ABat D and (AD)(BD)=11, then find the area of triangle ABC..
View SolutionletABC be a right angled triangle at C.If the inscribed circle touches the side ABat D and (AD)(BD)=11, then find the area of triangle ABC..
View SolutionIn given figure, ABC is a triangle right angled at B and BD⊥AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
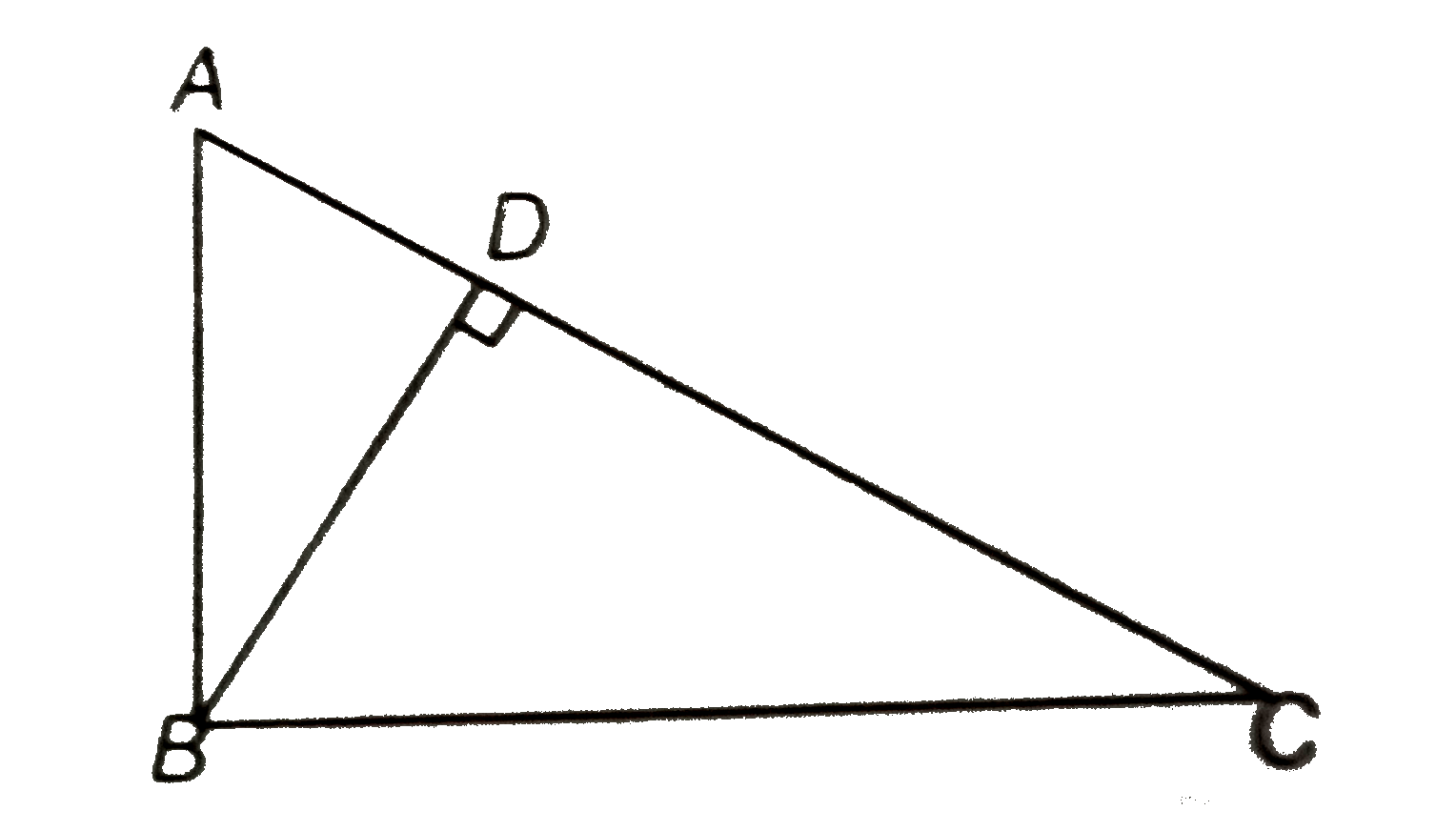
View SolutionIn triangle ABC,∠ABC−90∘,AB=2a+1andBC=2a2+2a. Find AC in terms of 'a' if a= 8 , find the lengths of the sides of the triangles.
View SolutionΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View SolutionIn ΔABC, If ∠C=3∠A,BC=27,andAB=48. Then the value of AC is ______
View SolutionIn triangle ABC, ∠B=90∘ and tan A = 0.75 If AC = 30 cm, find the lengths of AB and BC.
View Solution
