A triangle has base 10 cm long and the base angles of 50∘and70∘. If the perimeter of the triangle is x+ycosz∘ where z∈(0,90) then the value of x+y+z equals :
To solve the problem, we will follow these steps:
Step 1: Identify the Angles
Given a triangle with base angles of 50∘ and 70∘, we can find the third angle using the fact that the sum of angles in a triangle is 180∘.
Angle A=180∘−(50∘+70∘)=180∘−120∘=60∘
Step 2: Label the Sides
Let:
- Side a (opposite angle A) = 10 cm (the base)
- Side b (opposite angle B) = ?
- Side c (opposite angle C) = ?
Step 3: Apply the Sine Rule
According to the sine rule:
asinA=bsinB=csinC
Substituting the known values:
10sin60∘=bsin50∘=csin70∘
Step 4: Calculate Side b
Using the sine rule for sides a and b:
10sin60∘=bsin50∘
Rearranging gives:
b=10⋅sin50∘sin60∘
Using sin60∘=√32:
b=10⋅sin50∘√32=20sin50∘√3
Step 5: Calculate Side c
Using the sine rule for sides a and c:
10sin60∘=csin70∘
Rearranging gives:
c=10⋅sin70∘sin60∘
Thus:
c=10⋅sin70∘√32=20sin70∘√3
Step 6: Calculate the Perimeter
The perimeter P of the triangle is:
P=a+b+c=10+20sin50∘√3+20sin70∘√3
Factoring out 20√3:
P=10+20√3(sin50∘+sin70∘)
Step 7: Use the Sine Addition Formula
We can use the sine addition formula:
sinC+sinD=2sin(C+D2)cos(C−D2)
Setting C=50∘ and D=70∘:
sin50∘+sin70∘=2sin(60∘)cos(10∘)
Substituting this back into the perimeter equation:
P=10+20√3⋅2sin(60∘)cos(10∘)
Since sin(60∘)=√32:
P=10+20√3⋅2⋅√32⋅cos(10∘)
This simplifies to:
P=10+20cos(10∘)
Step 8: Identify x, y, and z
From the expression for the perimeter:
P=x+ycosz
We can identify:
- x=10
- y=20
- z=10∘
Step 9: Calculate x+y+z
Now we can find:
x+y+z=10+20+10=40
Final Answer
Thus, the value of x+y+z is:
40
Given a triangle with base angles of 50∘ and 70∘, we can find the third angle using the fact that the sum of angles in a triangle is 180∘.
Let:
- Side a (opposite angle A) = 10 cm (the base)
- Side b (opposite angle B) = ?
- Side c (opposite angle C) = ?
According to the sine rule:
Using the sine rule for sides a and b:
Using the sine rule for sides a and c:
The perimeter P of the triangle is:
We can use the sine addition formula:
From the expression for the perimeter:
- x=10
- y=20
- z=10∘
Now we can find:
Thus, the value of x+y+z is:
Topper's Solved these Questions
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-2 : One or More than One Answer is/are Correct15videos
SOLUTION OF TRIANGLES
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-3 : Comprehension Type Problems13videos
SOLUTION OF TRIANGLES
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)21videos
SEQUENCE AND SERIES
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-5 : Subjective Type Problems10videos
STRAIGHT LINES
Similar Questions
Knowledge Check
- Question 1 - Select One
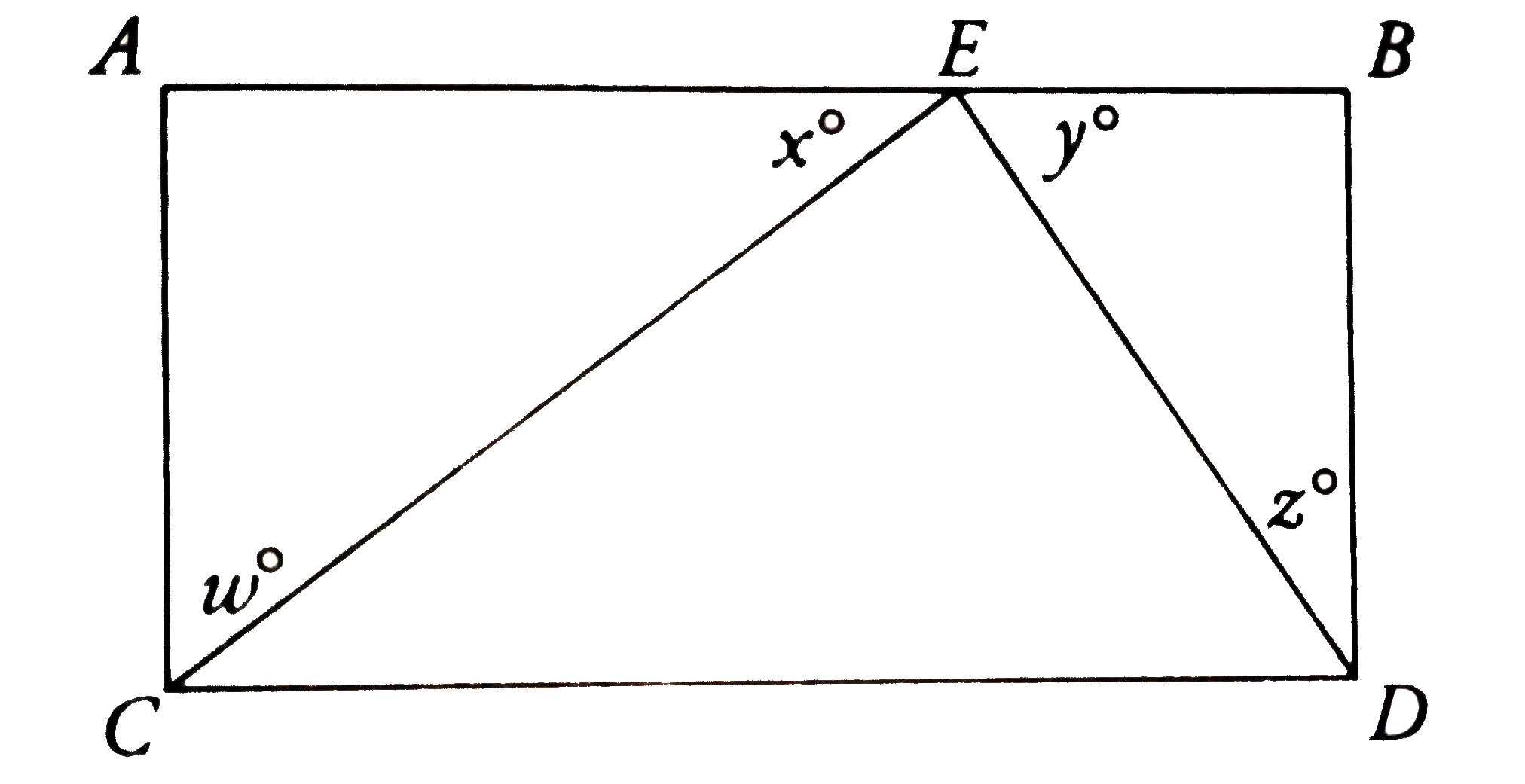
In ABCD is a triangle, what is the value of w+x+y+z?A90B150C180D210
A point 'P' is an arbitrary interior point of an equilateral triangle of side 4. If x, y, z are the distances of 'P' from sides of the triangle then the value of (x+y+z)2 is equal to -
View SolutionIf x,yandz are positive integers such that x<y<zandx+y+z=6, then what is the value of z?
View SolutionIf x,y and z are posirive real umbers and x=12−yzy+z . The maximum value of xyz equals.
View SolutionIf the lattice point P(x,y,z),x,y,z>oandx,y,z∈I with least value of z such that the 'p' lies on the planes 7x+6y+2z=272andx−y+z=16, then the value of (x+y+z−42) is equal to
View SolutionThe points A(x,y),B(y,z) and C(z,x) represents the vertices of a right angled triangle, if
View Solution
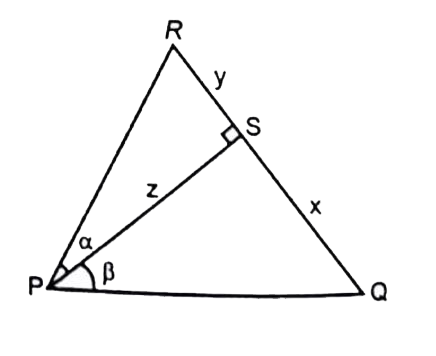
Two isosceles triangle are shown above. If 180-z=2y and y=75, what is the value of x?View SolutionIn a ΔPQR (as shown in figure) if x:y:z=2:3:6, then the value of ∠QPR is :
 View Solution
View Solution

