If a, b, c, x, y, z are real and a2+b2+c2=25,x2+y2+z2=36andax+by+cz=30, then a+b+cx+y+z is equal to :
1
65
56
34
The correct Answer is:C
To solve the problem step by step, we need to find the value of (a+b+c)/(x+y+z) given the conditions:
1. a2+b2+c2=25
2. x2+y2+z2=36
3. ax+by+cz=30
Step 1: Analyze the equations
We have three equations to work with. The first two equations represent the squares of the magnitudes of vectors in 3D space, and the third equation represents the dot product of these vectors.
Step 2: Choose values for b and c
To simplify our calculations, we can assume b=0 and c=0. This gives us:
- From a2+b2+c2=25, we have:
a2=25⟹a=±5
Step 3: Choose values for y and z
Similarly, we can assume y=0 and z=0. This gives us:
- From x2+y2+z2=36, we have:
x2=36⟹x=±6
Step 4: Check the dot product condition
Now we need to check if these values satisfy the dot product condition ax+by+cz=30:
- Substituting a=5 and x=6:
ax+by+cz=5⋅6+0+0=30
This condition is satisfied.
Step 5: Calculate (a+b+c)/(x+y+z)
Now we can substitute the values we have:
- a+b+c=5+0+0=5
- x+y+z=6+0+0=6
Thus,
a+b+cx+y+z=56
Step 6: Consider negative values
If we consider the negative values a=−5 and x=−6, we still find:
(−5)+0+0=−5
(−6)+0+0=−6
Thus,
−5−6=56
Final Answer
The value of a+b+cx+y+z is 56.
2. x2+y2+z2=36
3. ax+by+cz=30
We have three equations to work with. The first two equations represent the squares of the magnitudes of vectors in 3D space, and the third equation represents the dot product of these vectors.
To simplify our calculations, we can assume b=0 and c=0. This gives us:
- From a2+b2+c2=25, we have:
a2=25⟹a=±5
Similarly, we can assume y=0 and z=0. This gives us:
- From x2+y2+z2=36, we have:
x2=36⟹x=±6
Now we need to check if these values satisfy the dot product condition ax+by+cz=30:
- Substituting a=5 and x=6:
ax+by+cz=5⋅6+0+0=30
This condition is satisfied.
Now we can substitute the values we have:
- a+b+c=5+0+0=5
- x+y+z=6+0+0=6
a+b+cx+y+z=56
If we consider the negative values a=−5 and x=−6, we still find:
(−5)+0+0=−5
(−6)+0+0=−6
Thus,
−5−6=56
The value of a+b+cx+y+z is 56.
Topper's Solved these Questions
- VECTOR & 3DIMENSIONAL GEOMETRYBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-2 : One or More than One Answer is/are Correct
20 Videos
- VECTOR & 3DIMENSIONAL GEOMETRYBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-3 : Comprehension Type Problems
12 Videos
- TRIGONOMETRIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems
9 Videos
Similar Questions
If xa=yb=zcandy2=xz, prove that b=2aca+c
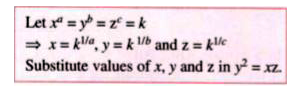
View SolutionIf a2+b2+c2=x2+y2+z2=1, then show that ax+by+cz≤1.
View SolutionIf a, b, c are positive integers, then
(a2+b2+c2a+b+c)a+b+c>axbycz, then
View SolutionIf a = b2x,b=c2yandc=a2z, show that 8xyz = 1.
View SolutionIf ax=by=cz and b2=ac, then show that y=2zxz+x
View SolutionIf y2=xzandax=by=cz, then prove that (log)ab=(log)bc
View SolutionIf x,y,z are real and 4x2+9y2+16z2−6xy−12yz−8zx=0,thenx,y,z are in a. A.P. b. G.P. c. H.P. d. none of these
View SolutionIf a,b,c,d,e, and fare in G.P. then the value of ∣∣ ∣ ∣∣(a2)(d2)x(b2)(e2)y(c2)(f2)z∣∣ ∣ ∣∣ depends on (A) x and y (B) x and z (C) y and z (D) independent of x ,y ,and z
View SolutionIf x = 6a + 8b + 9c, y = 2b - 3a - 6c and z = c - b + 3a, find :
x+y+z
View SolutionIf x = 6a + 8b + 9c, y = 2b - 3a - 6c and z = c - b + 3a, find :
x−y+z
View Solution
