If be four real members of same sign, then the minimum value of is : (a) 6 (b) 8 (c) 12 (d) 24
6
8
12
24
The correct Answer is:C
To solve the problem, we need to find the minimum value of the expression:
S=4∑i=14∑j=1,j≠iaiaj
This expression can be expanded as follows:
1. Expand the expression:
S=a1a2+a1a3+a1a4+a2a1+a2a3+a2a4+a3a1+a3a2+a3a4+a4a1+a4a2+a4a3
2. Group the terms:
Notice that for each pair (i,j), we have both aiaj and ajai. For example, a1a2+a2a1.
3. Apply the AM-GM inequality:
For each pair aiaj+ajai, by the AM-GM inequality:
aiaj+ajai≥2
4. Count the pairs:
There are a total of 12 pairs (since there are 4 values of ai and each can pair with 3 others). Each pair contributes at least 2 to the sum.
5. Calculate the minimum value:
Since there are 6 pairs of the form aiaj+ajai, the minimum value of S is:
S≥6×2=12
Thus, the minimum value of S is 12.
Final Answer:
The minimum value of ∑aiaj for i≠j is 12 (Option C).
S=a1a2+a1a3+a1a4+a2a1+a2a3+a2a4+a3a1+a3a2+a3a4+a4a1+a4a2+a4a3
Notice that for each pair (i,j), we have both aiaj and ajai. For example, a1a2+a2a1.
For each pair aiaj+ajai, by the AM-GM inequality:
aiaj+ajai≥2
There are a total of 12 pairs (since there are 4 values of ai and each can pair with 3 others). Each pair contributes at least 2 to the sum.
Since there are 6 pairs of the form aiaj+ajai, the minimum value of S is:
S≥6×2=12
The minimum value of ∑aiaj for i≠j is 12 (Option C).
Topper's Solved these Questions
- SEQUENCE AND SERIES Book:VK JAISWAL ENGLISHChapter:SEQUENCE AND SERIES Exercise:EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)
Explore 19 Videos
- SEQUENCE AND SERIES Book:VK JAISWAL ENGLISHChapter:SEQUENCE AND SERIES Exercise:EXERCISE (COMPREHENSION TYPE PROBLEMS)
Explore 17 Videos
- QUADRATIC EQUATIONS Book:VK JAISWAL ENGLISHChapter:QUADRATIC EQUATIONS Exercise:EXERCISE (SUBJECTIVE TYPE PROBLEMS)
Explore 43 Videos
- SOLUTION OF TRIANGLESBook:VK JAISWAL ENGLISHChapter:SOLUTION OF TRIANGLESExercise:Exercise-5 : Subjective Type Problems
Explore 9 Videos
Similar Questions
If ai>0 for i=1,2,…., n and a1a2 … an=1 , then minimum value of (1+a1)(1+a2) ….. (1+an) is :
View SolutionThe circle orthogonal to the three circles x2+y2+aix+biy+c=0, (i=1,2,3) is
View SolutionWhat is the value of ∑i+j=odd1≤|<|≤10(i+j)−∑i+j=even1≤|<|≤10(i+j) ?
View SolutionFor a 2×2 matrix A=[aij] whose elements are given by aij=ij , write the value of a12 .
View SolutionIf matrix A=([aij])2×2 , where aij={1, if i≠j0, if i=j , then A2 is equal to I (b) A (c) O (d) I
View SolutionIn given figure →AB=3ˆi−ˆj,→AC=2ˆi+3ˆj and DE=4ˆi−2ˆj . Then the area of the shaded region is
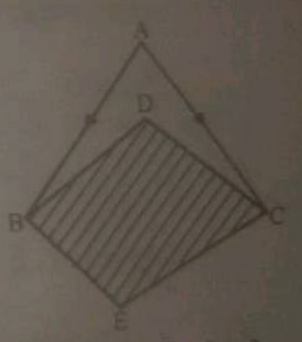
(a)5 (b) 6 (c) 7 (d)(8)
View SolutionThe positon vector of the centroid of the triangle ABC is 2i+4j+2k. If the position vector of the vector A is 2i+6j+4k.,thentheposition→−−→rofm∮ofBCis(A)2i+3j+k(B)2i+3jk(C)2i-3j-k(D)-2i-3j-k
View SolutionLet P=[aij] be a 3×3 matrix and let Q=[bij],wherebij=2i+jaijfor1≤i,j≤3. If the determinant of P is 2, then the determinant of the matrix Q is 210 b. 211 c. 212 d. 213
View Solutiona1,a2,a3 ,…., an from an A.P. Then the sum 10∑i=1aiai+1ai+2ai+ai+2 where a1=1 and a2=2 is :
View SolutionThe unit vector parallel to the resultant of the vectors A = 4i+3j + 6k and B = -i + 3j-8k is
View Solution