Let $f (x) = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots \dots \dots + \frac{1}{n}$ such that $P (n) f (n + 2) = P (n) f (n) + q (n) .$ Where $P (n) Q (n)$ are polynomials of least possible degree and $P (n)$ has leading coefficient unity. Then match the following Column-I with Column-II.

Video Solution

Text Solution

Verified by Experts

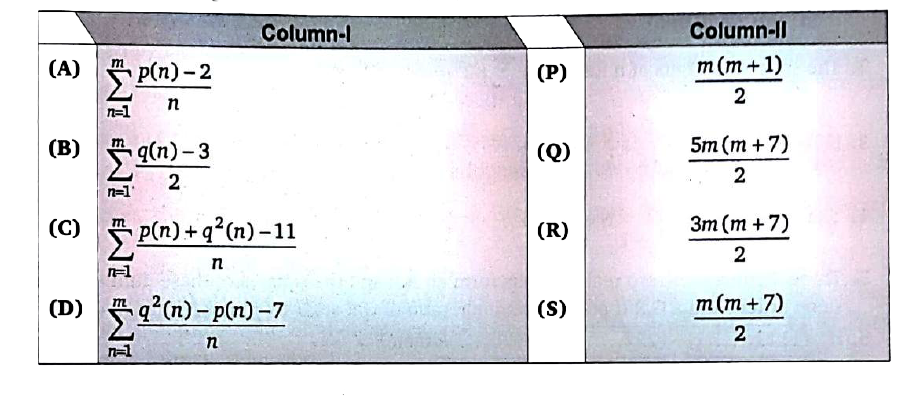
The correct Answer is: $A \to S; B \to P; C \to Q; D \to R$

Updated on:21/07/2023

Answer

Step by step video & image solution for Let f (x) =1+ 1/2+ 1/3+ 1/4 + ……… + 1/n such that P (n) f (n+2) = P ( n) f (n) + q (n). Where P (n) Q(n) are polynomials of least possible degree and P (n) has leading coefficient unity. Then match the following Column-I with Column-II. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS SEQUENCE AND SERIES

Topper's Solved these Questions

Knowledge Check

Let $P (n) : (2 n + 1) < 2^{n}$ , then the smallest positive integer for which P(n) is true?
A(a)2
B(b)3
C(c)4
D(d)5

VK JAISWAL ENGLISH-SEQUENCE AND SERIES -EXERCISE (MATCHING TYPE PROBLEMS)

Home
Ask Doubt
Profile

Let f(x)=1+12+13+14+………+1n such that P(n)f(n+2)=P(n)f(n)+q(n). Where P(n)Q(n) are polynomials of least possible degree and P(n) has leading coefficient unity. Then match the following Column-I with Column-II.

The correct Answer is:A→S;B→P;C→Q;D→R

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let P(n):(2n+1)<2n, then the smallest positive integer for which P(n) is true?

VK JAISWAL ENGLISH-SEQUENCE AND SERIES -EXERCISE (MATCHING TYPE PROBLEMS)

Let $f (x) = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots \dots \dots + \frac{1}{n}$ such that $P (n) f (n + 2) = P (n) f (n) + q (n) .$ Where $P (n) Q (n)$ are polynomials of least possible degree and $P (n)$ has leading coefficient unity. Then match the following Column-I with Column-II.

The correct Answer is: $A \to S; B \to P; C \to Q; D \to R$

Let $P (n) : (2 n + 1) < 2^{n}$ , then the smallest positive integer for which P(n) is true?