Let $Δ = ∣ ∣ ∣ ∣ \begin{matrix} a & a + d & a + 3 d a + d & a + 2 d & a a + 2 d & a & a + d \end{matrix} ∣ ∣ ∣ ∣$ then :

$Δ$ depends on a

$Δ$ depends on d

$Δ$ is independent of a,d

$Δ = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B

Updated on:21/07/2023

Answer

Step by step video & image solution for Let Delta=|{:(a,a+d,a+3d),(a+d,a+2d,a),(a+2d, a, a+d):}| then : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS DETERMINANTS

Topper's Solved these Questions

DETERMINANTSBOOK - VK JAISWAL ENGLISHCHAPTER - DETERMINANTSEXERCISE - EXERCISE-3:COMPREHENSION TYPE PROBLEMS
3 Videos
DETERMINANTSBOOK - VK JAISWAL ENGLISHCHAPTER - DETERMINANTSEXERCISE - EXERCISE-4 : SUBJECTIVE TYPE PROBLEMS
12 Videos
DETERMINANTSBOOK - VK JAISWAL ENGLISHCHAPTER - DETERMINANTSEXERCISE - EXERCISE-4 : SUBJECTIVE TYPE PROBLEMS
12 Videos
CONTINUITY, DIFFERENTIABILITY AND DIFFERENTIATIONBOOK - VK JAISWAL ENGLISHCHAPTER - CONTINUITY, DIFFERENTIABILITY AND DIFFERENTIATIONEXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
22 Videos
DIFFERENTIAL EQUATIONSBOOK - VK JAISWAL ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
6 Videos

Similar Questions

If $∣ ∣ ∣ ∣ ∣ \begin{matrix} a & a + d & a + 2 d a^{2} & {(a + d)}^{2} & {(a + 2 d)}^{2} 2 a + 3 d & 2 (a + d) & 2 a + d \end{matrix} ∣ ∣ ∣ ∣ ∣ = 0$ , then
View Solution
let $a > 0, d > 0$ find the value of the determinant $∣ ∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} \frac{1}{a} & \frac{1}{a (a + d)} & \frac{1}{(a + d) (a + 2 d)} \frac{1}{a + d} & \frac{1}{(a + d) (a + 2 d)} & \frac{1}{(a + 2 d) (a + 3 d)} \frac{1}{a + 2 d} & \frac{1}{(a + 2 d) (a + 3 d)} & \frac{1}{(a + 3 d) (a + 4 d)} \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣ ∣$
View Solution
Let $D_{1} = ∣ ∣ ∣ ∣ \begin{matrix} a & b & a + b c & d & c + d a & b & a - b \end{matrix} ∣ ∣ ∣ ∣$ and $D_{2} = ∣ ∣ ∣ ∣ \begin{matrix} a & c & a + c b & d & b + d a & c & a + b + c \end{matrix} ∣ ∣ ∣ ∣$ then the value of $∣ ∣ ∣ \frac{D_{1}}{D_{2}} ∣ ∣ ∣$ , where $b \neq 0$ and $a d \neq b c,$ is _____.
View Solution
A particle just clears a wall of height b at distance a and strikes the ground at a distance c from the point of projection. The angle of projection is (1) $\frac{{tan}^{- 1} b}{a c}$ (2) $45^{o}$ (3) $\frac{{tan}^{- 1} (b c)}{a (c - a)}$ (4) $\frac{{tan}^{- 1} (b c)}{a}$
View Solution
Let A and B be two sets such that $n (A) = 5 a n d n (B) = 2, if a, b, c, d, e$ are distinct and $(a, 2), (b, 3), (c, 2), (d, 3), (e, 2)$ are in $A \times B$ , find A and B.
View Solution
The standard deviation of a, a+d, a + 2d,….a + 2nd is
View Solution
Let $D_{1} = | a b a + b c d c + d a b a - b | a n d D_{2} = | a c a + c b d b + d a c a + b + c |$ then the value of $∣ ∣ ∣ \frac{D_{1}}{D_{2}} ∣ ∣ ∣, w h e r e b \neq 0 a n d a d \neq b c,$ is _____.
View Solution
Let $A = [\begin{matrix} 1 & 0 2 & 3 \end{matrix}] and A^{n} = [\begin{matrix} a & b c & d \end{matrix}]$ then $lim n \to \infty \frac{b + c}{a + d}$ =
View Solution
If the area of each plate is A and then successive separations are $d, 2 d$ and $3 d$ , then find the equivalent capacitance across A and B.
.
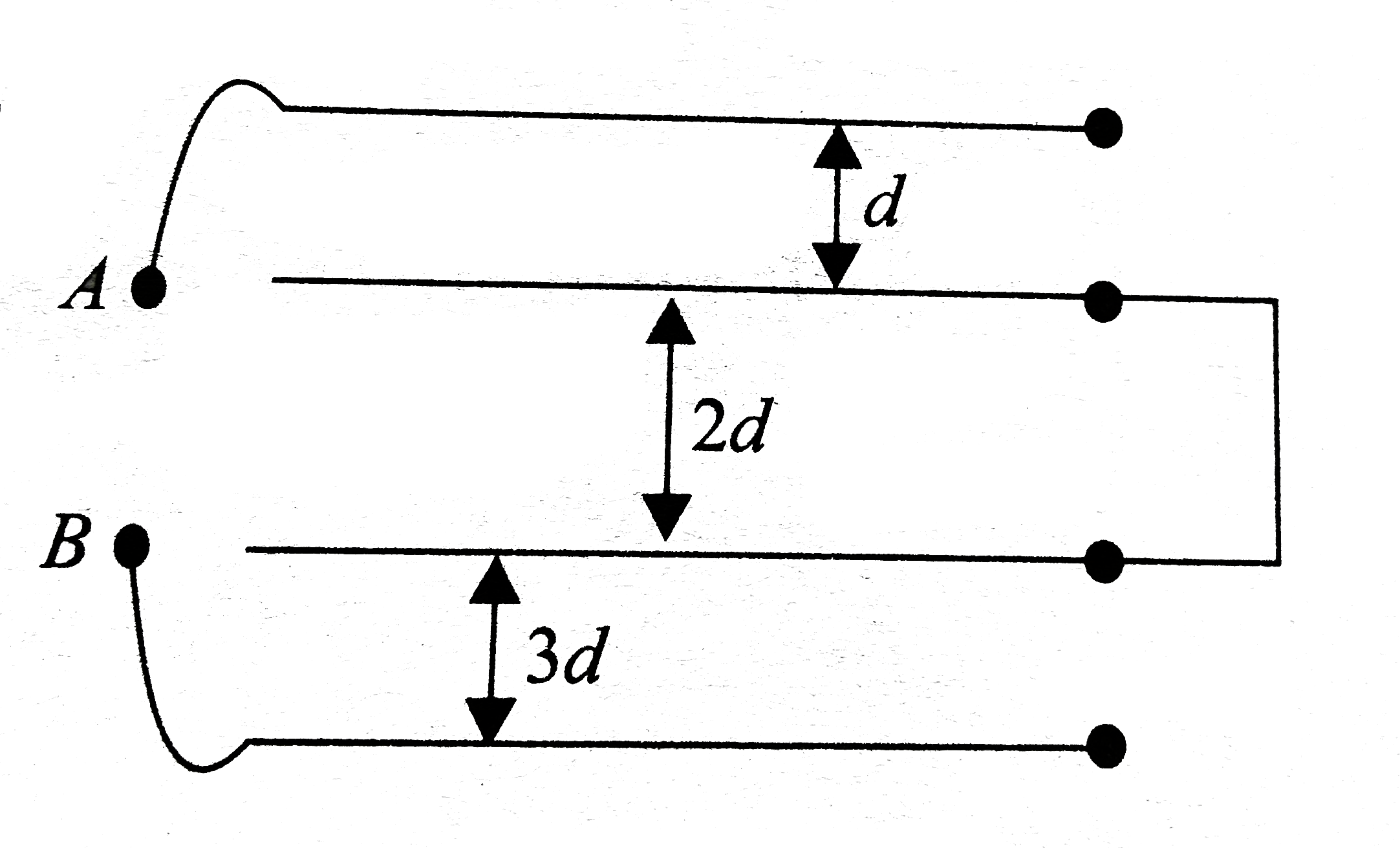View Solution
Let $d \in R, and A ⎡ ⎢ ⎣ \begin{matrix} - 2 & 4 + d & (sin θ - 2) 1 & (sin θ) + 2 & d 5 & (2 sin θ) d & (- sin θ) + 2 + 2 d \end{matrix} ⎤ ⎥ ⎦ = θ \in [0, 2 π]$ If the minimum value of det(A) is B. Then the value of d is:
View Solution

VK JAISWAL ENGLISH-DETERMINANTS-EXERCISE-2 : ONE OR MORE THAN ONE ANSWER IS / ARE CORRECT

Delta = |(a, a^2, 0),(1, 2a+b,(a+b)),(0, 1, 2a+3b)| is divisible by a....
04:05
If |{:(1+cos^2 theta, sin^2 theta, 2sqrt3tantheta),(cos^2 theta, 1+sin...
02:31
Let Delta=|{:(a,a+d,a+3d),(a+d,a+2d,a),(a+2d, a, a+d):}| then :
01:59
The value(s) of lambda for which the system of equations (1-lambda)...
07:04
Let D(x)=|{:(x^2+4x-3, 2x+4,13),(2x^2+5x-9,4x+5,26),(8x^2-16x+1, 16x-6...
04:41
if the system of equations {:(ax+y+2z=0),(x+2y+z=b),(2x+y+az=0):} ...
11:26

Home
Ask Doubt
Profile

Let Δ=∣∣ ∣∣aa+da+3da+da+2daa+2daa+d∣∣ ∣∣ then :

The correct Answer is:A, B

Topper's Solved these Questions

Similar Questions

VK JAISWAL ENGLISH-DETERMINANTS-EXERCISE-2 : ONE OR MORE THAN ONE ANSWER IS / ARE CORRECT

Let $Δ = ∣ ∣ ∣ ∣ \begin{matrix} a & a + d & a + 3 d a + d & a + 2 d & a a + 2 d & a & a + d \end{matrix} ∣ ∣ ∣ ∣$ then :