You are given a rod of length L. The linear mass density is λ such that λ=a+bx. Here a and b are constants and the mass of the rod increases as x decreases. Find the mass of the rod

We are not calculated the mass of the rod simply multiplying linear mass density λ will the length of the rod as λ is not constant.
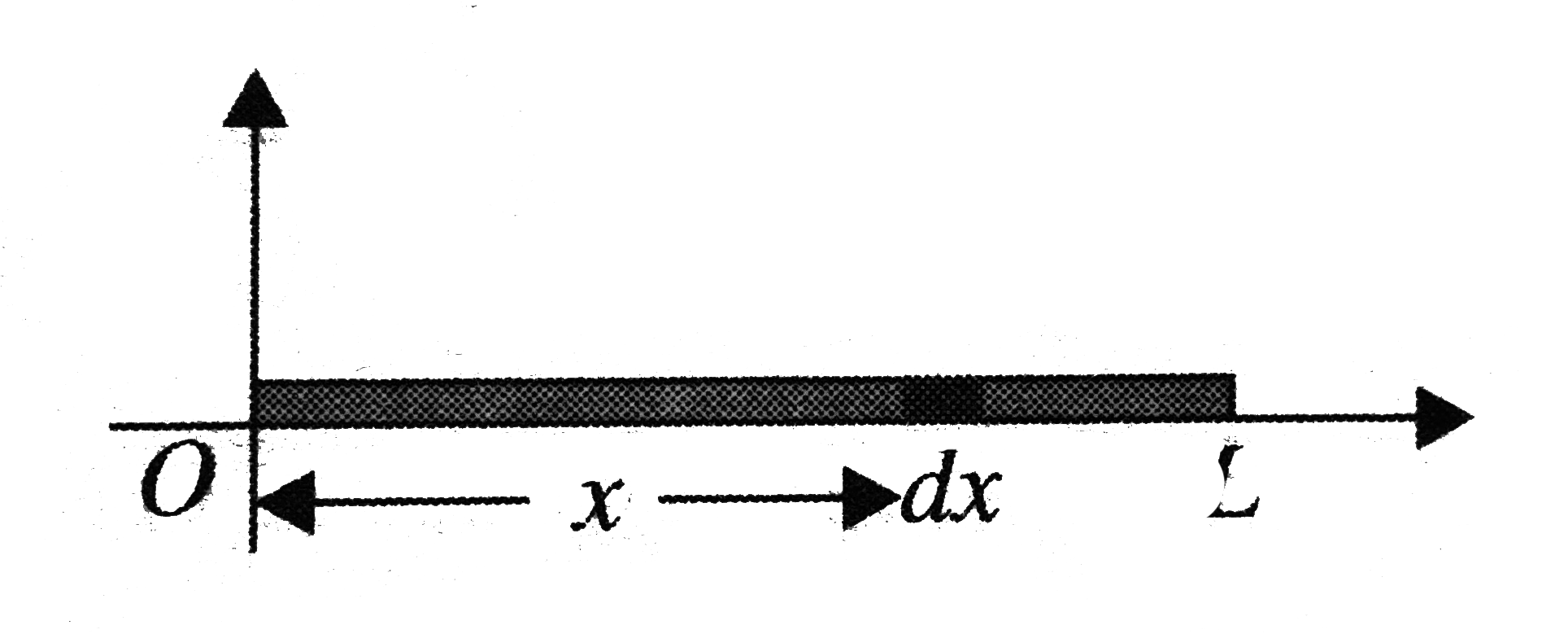
Hence, we have to divide entire rod length into a number of elements and add the mass of the elements.
M=dm1+dm2+dm3+...
This step can be written in terms of integration.
M=∫dm
If we take an element dx on the rod at a distance x from the left end of the rod.

Mass of this element dm=λ.dx
dm=(a+bx)dx
Hence, total mass,
M=∫dm=L∫0(a+bx)dx
=L∫0adx+L∫0bxdx
=aL∫0dx+bL∫0xdx
=a[x]L0+b[x22]L0=aL+bL22
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.12videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.23videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer4videos
ARCHIVES 2 VOLUME 6
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
Similar Questions
Find coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. Here, a and b are constants. Find the position of centre of mass of this rod.
View Solution
Knowledge Check
- Question 1 - Select One
The density of a non-uniform rod of length 1m is given by ρ(x)=a(1+bx2)
where a and b are constants and 0≤x≤1.
The centre of mass of the rod will be atA3(2+b)4(3+b)B4(2+b)3(3+b)C3(3+b)4(2+b)D4(3+b)3(2+b)
The linear density of a non−uniform rod of length 2m is given by λ(x)=a(1+bx2) where a and b are constants and 0≤x≤2. The centre of mass of the rod will be at. X=
View SolutionThe linear mass density lambda of a rod AB is given by λ=α+βx kg/m taking O as origin. Find the location of the centre of mass from the end A?
View SolutionA large sheet carries uniform surface charge density σ . A rod of length 2l has a linear charge density λ on one half and −λ on the second half. The rod is hinged at the midpoint O and makes an angle θ with the normal to the sheet. The torque experience by the rod is
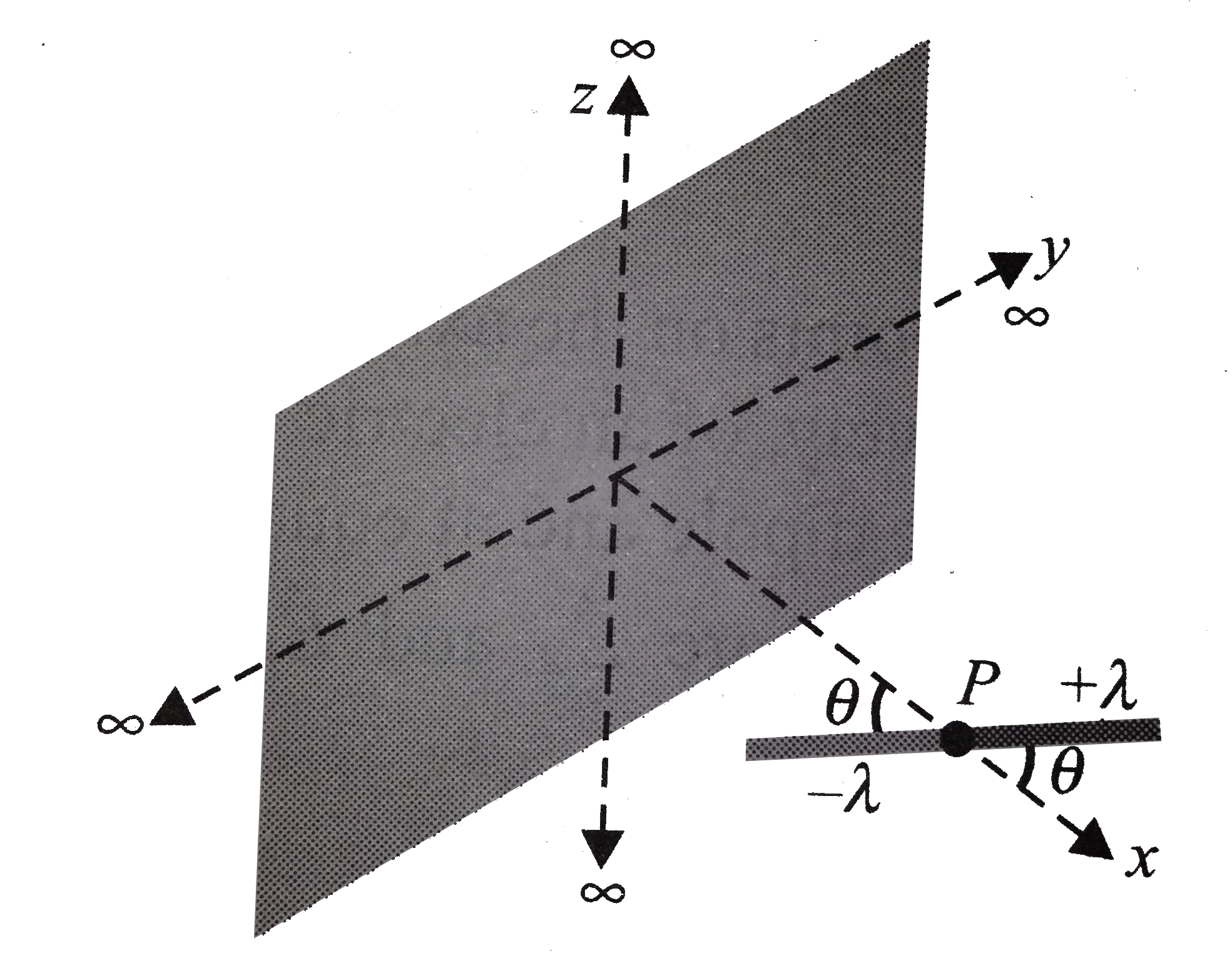 View Solution
View SolutionFind centre of mass of given rod of linear mass density λ=(a+b(xl)2) , x is distance from one of its end. Length of the rod is l.
View SolutionA uniform thin rod AB of length L has linear mass density μ(x)=a+bxL, where x is measured from A. If the CM of the rod lies at a distance of (712L) from A, then a and b are related as :_
View SolutionA heavy metallic rod of non-uniform mass distribution, is hanged vertically from a rigid support. The linear mass density varies as λ(x)=k×x where x is the distance measured along the length of rod, from its lower end. Find extension in rod due to its own weight.
View SolutionThe density of a non-uniform rod of length 1m is given by ρ(x)=a(1+bx2)
where a and b are constants and 0≤x≤1.
The centre of mass of the rod will be atView Solution

