A particle slides with a speed of 3ms−1 at P. When it reaches Q,it acquires a speed of 4ms−1 after describing an angle of 60∘ at O as shown in figure .Find the changes in the velocity of the particle between P and Q. Assume that the path followed by the particle is circular from P to Q

As the particle moves from P to Q, its speed increases from v1=3ms−1 to v2=4ms−1 and the angle described by the velocity vector is equal to θ=60∘.Then the change in velocity is given as
Δv=√v21+v22−2v1v2cosθ
Substituting, v1=3ms−1,v2=4ms−1 and θ=60∘ in the above expression ,we have
Δv=√32+42−2.3.4cos60∘
This yield Δv=√13ms−1 and the change in velocity is directed as shown in figure
 .
.
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 3.1
19 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 3.2
13 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
Knowledge Check
A particle is moving on a circular path of radius r with uniform speed v. What is the displacement of the particle after it has described an angle of 60∘?
Ar√2Br√3CrD2r
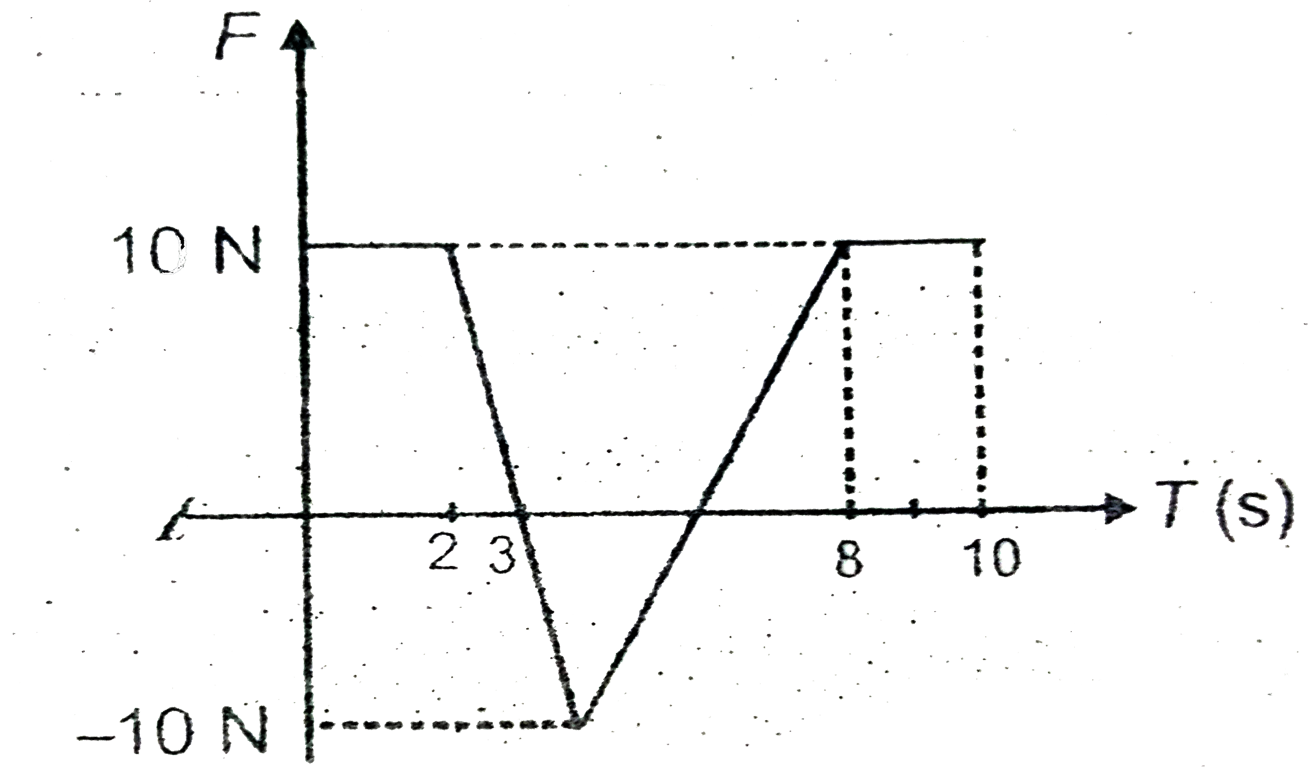
A time varying force acts on a particle of mass 5 kg as shown in figure . Find the speed of the particle, in m/s , after 10 s , if particle was intially at rest .
View SolutionA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is

View SolutionA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is

View SolutionA particle is moving on a circular path with constant speed v. The magnitude of the change in its velocity after it has described an angle of 90∘ is :
View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .

View SolutionA particle is projected with speed 20ms−1 at an angle 30∘ With horizontal. After how much time the angle between velocity and acceleration will be 90∘
View SolutionA particle is projected at an angle of 60∘ above the horizontal with a speed of 10m/s. After some time the direction of its velocity makes an angle of 30∘ above the horizontal. The speed of the particle at this instant is
View Solution