Given that →A+→B+→C=→0. Out of three vectors,two are equal in magnitude and the magnitude of the third vectors is √2 times that of either of the two having equal magnitude. Find the angles between the vectors.
Given
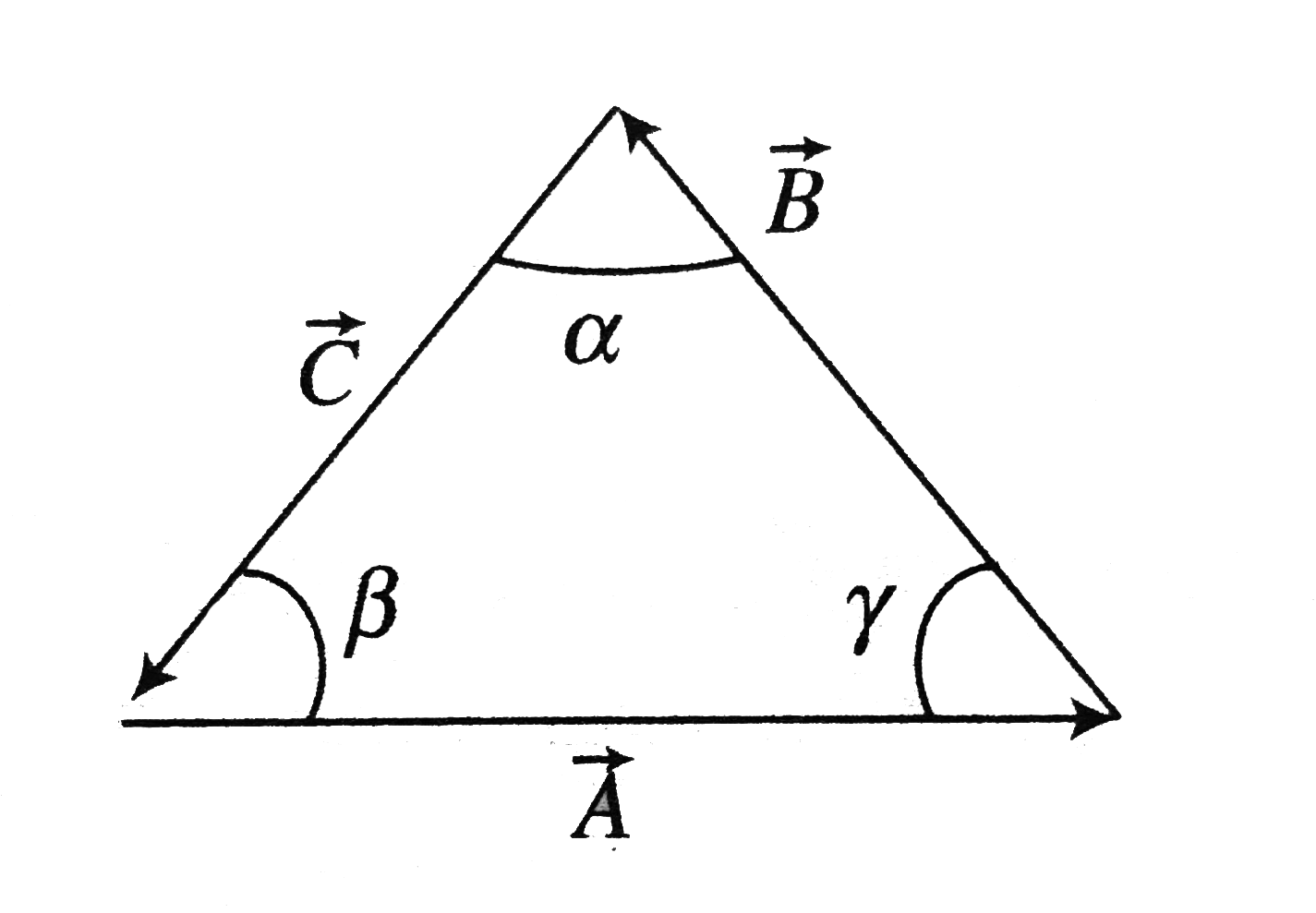
A=B,C=√2A=√2B.
From (figure) α=β and α+β+γ=180∘
⇒γ=180∘−2α
Apply Lami's theorem: Asinα=Csinγ
⇒Asinα=√2Asinα(180−2α)
⇒1sinα=√2sin2α
1sinα=√22sinαcosα⇒cosα=1√2⇒α=45∘
⇒β=45∘ and γ=180∘−2α=90∘
Angle between →A and →B=180∘−γ=90∘,
Angle between →B and →C=180−α=135∘,
Angle between →C and →A=180∘−β=135∘.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 3.119videos
VECTORS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 3.213videos
VECTORS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)4videos
WORK, POWER & ENERGY
Similar Questions
Given that →A+→B+→C=0, out of three vectors two are equal in magnitude and the magnitude of third vector is √2 times that of either of two having equal magnitude. Then angle between vectors are given by
View SolutionGiven that P+Q+R= 0. Two out of the three vectors are equal in magnitude. The magnitude fo the third vector is s √2 times that of the other two. Which of the following can be the angles between these vectors?
View SolutionTwo vectors of equal magnitude are acting through a point. The magnitude of resultant is equal to the magnitude of either vectoe. Find the angle between the vectors.
View SolutionTwo vectors, both equal in magnitude, have their resultant equal in magnitude of the either. Find the angle between the two vectors.
View SolutionIf magnitude of the resultant of two vectors equal of magnitude, is equal to the magnitude of either of the vectors, what is the angle between them ?
View SolutionThe sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors −−→OBand−−→OC.
 View Solution
View SolutionTwo vectors →A and →B have equal magnitudes . If magnitude of →A+→B is equal to n× the magnitude of →A−→B , then the angle between →A and →B is
View SolutionFind the magnitude of two vectors →aand →b having the same magnitude and such that the angle between them is 600and their scalar product is 12.
View SolutionFind the magnitude of two vectors →a and →b having the same magnitude and such that the angle between them is 600 and their scalar product is 9/2 .
View SolutionThe sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
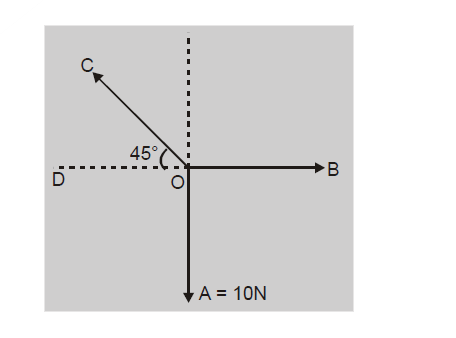
(ii) What is the magnitude of vector −−→OC ?View Solution

