ˆi and ˆj are unit vectors along x-and y-axes respectively. What is the magnitude and the direction of the vectors ˆi+ˆj and ˆi−ˆj? What are the components of a vector →A=2ˆi+3ˆj along the direction ˆi+ˆjand ˆi−ˆj?
Video Solution
Text Solution
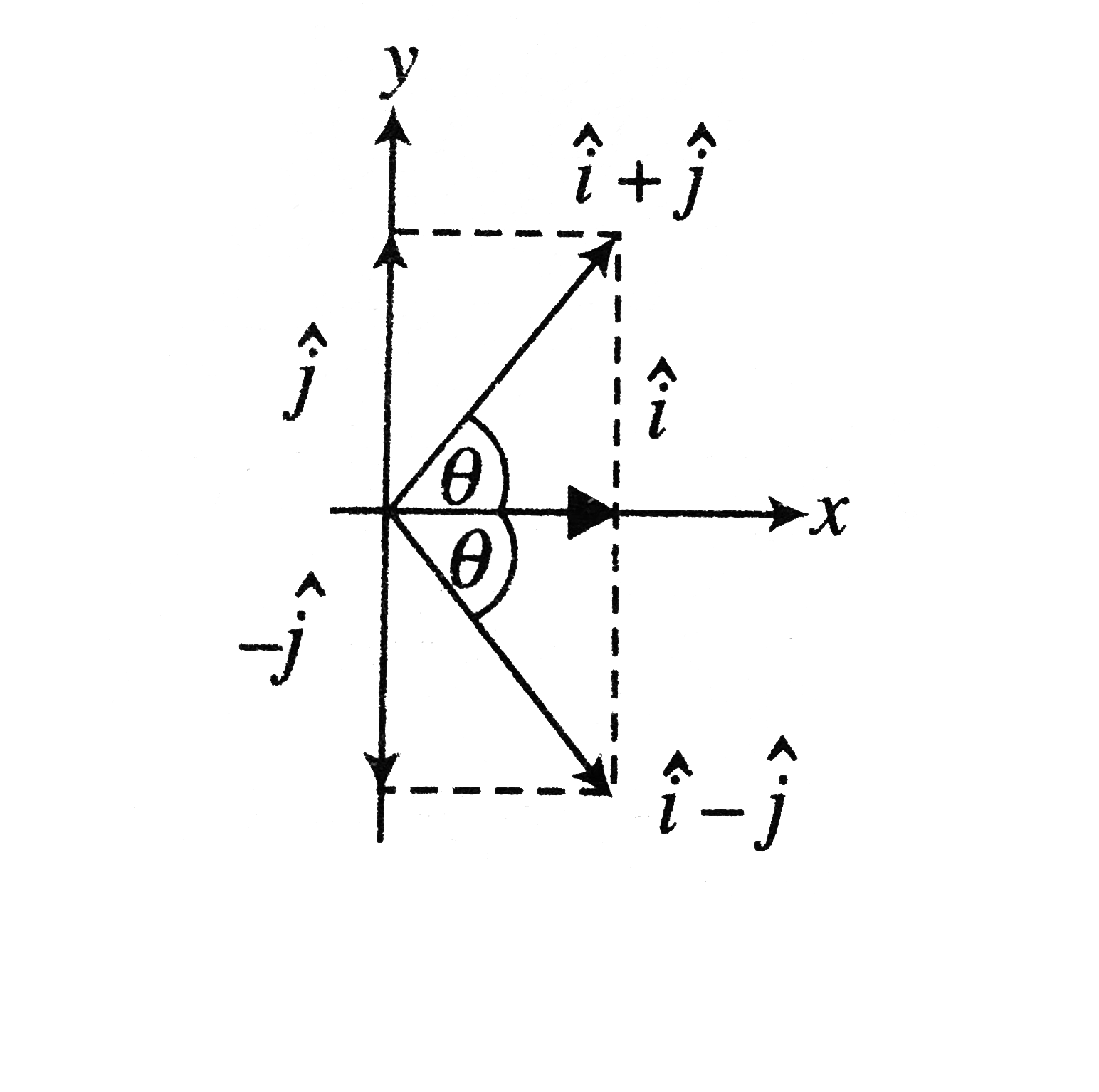
a.∣∣ˆi+ˆj∣∣=√12+12+2×1×1×cos90∘
=√2=1.414 units
tanθ=11=1
∴θ=45∘
So, the vector ˆi+ˆj makes an angle of 45∘ with x-axis.
b. ∣∣ˆi−ˆj∣∣=∣∣ˆi+(−ˆj)∣∣
=√12+(−1)2+2(1)(−1)cos90∘=√2
tanθ=1−1=−1∴θ=−45∘
The vector →A=2ˆi+3ˆj makes an angle of −45∘ with x=axis.
Let us know determine the component of →A=2ˆi+3ˆj in the direction of ˆi+ˆj.
Then, →B=ˆi+ˆj
→A.→B=ABcosθ=(Acosθ)B
So component of →A in the direction of →B
=→A⋅→BB=(2ˆi+3ˆj).(ˆi+ˆj)√12+12=2.1+3.1√2=5√2 units
Component of →A in the direction of ˆi−ˆj
(2ˆi+3ˆj).(ˆi−ˆj)√2=−1√2 units.
Here,PM is the component of →A in the direction of →B. So, dot product of two vectors →A and →B may be defined as the product of the magnitude of →B and the component of →Ain the direction →B.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 3.119videos
VECTORS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 3.213videos
VECTORS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)4videos
WORK, POWER & ENERGY
Similar Questions
Knowledge Check
- Question 1 - Select One
Unit vector along the vector ˆi+ˆj+ˆk is
A13(ˆi+ˆk+ˆk)B12(ˆi+ˆj+ˆk)C1√3(ˆi+ˆj+ˆk)D1√2(ˆi+ˆj+ˆk) - Question 2 - Select One
Unit vector perpendicular to the vectors ˆi−ˆj and ˆi+ˆj is
AˆkB−ˆkCˆi−ˆj√2Dˆi+ˆj√2 - Question 3 - Select One
The vector in the direction of the vector ˆi−2ˆj+2ˆk that has magnitude 9 units is
Aˆi−2ˆj+2ˆkBˆi−2ˆj+2ˆk3C3(ˆi−2ˆj+2ˆk)D9(ˆi−2ˆj+2ˆk)
The component of vector A=2ˆi+3ˆj along the vector ˆi+ˆj is
View SolutionThe component of the vector barĀ= (2hat i +3 hat j) along the vector ¯¯¯B=(ˆi+ˆj) is
View SolutionFind the projection of the vector ˆi−ˆjon the vector ˆi+ˆj
View SolutionFind the unit vector in the direction of the vector →a=ˆi+ˆj+ 2ˆk .
View SolutionIf ˆi,ˆj and ˆk represent unit vectors along the x, y and z axes respectively, then the angle θ between the vectors (ˆi+ˆj+ˆk) and (ˆi+ˆj) is equal to :
View Solution
