A particle at the edge of a ratating disc speeds up at a uniform angular acceleration ∝. If the radius of the disc is R, find the angular distance covered by the particle till its acquires a total acceleration a0.
To solve the problem, we need to find the angular distance covered by a particle at the edge of a rotating disc until it acquires a total acceleration a0. The disc has a uniform angular acceleration α and a radius R.
1. Understand Total Acceleration:
The total acceleration a0 of the particle in circular motion is the vector sum of tangential acceleration at and centripetal acceleration ac. This can be expressed as:
a20=a2t+a2c
2. Identify Tangential and Centripetal Acceleration:
- The tangential acceleration at is given by:
at=αR
- The centripetal acceleration ac is given by:
ac=v2R=(ωR)2R=ω2R
where ω is the angular velocity.
3. Substitute into the Total Acceleration Formula:
Substitute at and ac into the total acceleration equation:
a20=(αR)2+(ω2R)2
This simplifies to:
a20=α2R2+ω4R2
4. Relate Angular Velocity to Angular Distance:
Using the equation of motion for angular displacement, we have:
ω2=2αθ
where θ is the angular distance covered.
5. Substituting for ω2:
Substitute ω2 into the total acceleration equation:
a20=α2R2+(2αθ)2R2
This gives:
a20=α2R2+4α2θ2R2
6. Rearranging the Equation:
Factor out α2R2:
a20=α2R2(1+4θ2)
7. Solving for θ2:
Rearranging gives:
1+4θ2=a20α2R2
Thus:
4θ2=a20α2R2−1
Therefore:
θ2=a204α2R2−14
8. Taking the Square Root:
Finally, take the square root to find θ:
θ=√a204α2R2−14
Final Result:
The angular distance covered by the particle until it acquires a total acceleration a0 is:
θ=√a204α2R2−14
The total acceleration a0 of the particle in circular motion is the vector sum of tangential acceleration at and centripetal acceleration ac. This can be expressed as:
a20=a2t+a2c
- The tangential acceleration at is given by:
at=αR
- The centripetal acceleration ac is given by:
ac=v2R=(ωR)2R=ω2R
where ω is the angular velocity.
Substitute at and ac into the total acceleration equation:
a20=(αR)2+(ω2R)2
This simplifies to:
a20=α2R2+ω4R2
Using the equation of motion for angular displacement, we have:
ω2=2αθ
where θ is the angular distance covered.
Substitute ω2 into the total acceleration equation:
a20=α2R2+(2αθ)2R2
This gives:
a20=α2R2+4α2θ2R2
Factor out α2R2:
a20=α2R2(1+4θ2)
Rearranging gives:
1+4θ2=a20α2R2
Thus:
4θ2=a20α2R2−1
Therefore:
θ2=a204α2R2−14
Finally, take the square root to find θ:
θ=√a204α2R2−14
The angular distance covered by the particle until it acquires a total acceleration a0 is:
θ=√a204α2R2−14
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective40videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct76videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.312videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
A particle of mass M and radius of gyration K is rotating with angular acceleration α. The torque acting on the particle is
View SolutionA particle is at a distance r from the axis of rotation. A given torque τ produces some angular acceleration in it. If the mass of the particle is doubled and its distance from the axis is halved, the value of torque to produce the same angular acceleration is -
View SolutionA particle is moving around a circular path with uniform angular speed (x) . The radius of the circular path is (r). The acceleration of the particle is:
View SolutionRefering to v−s diagram, find:
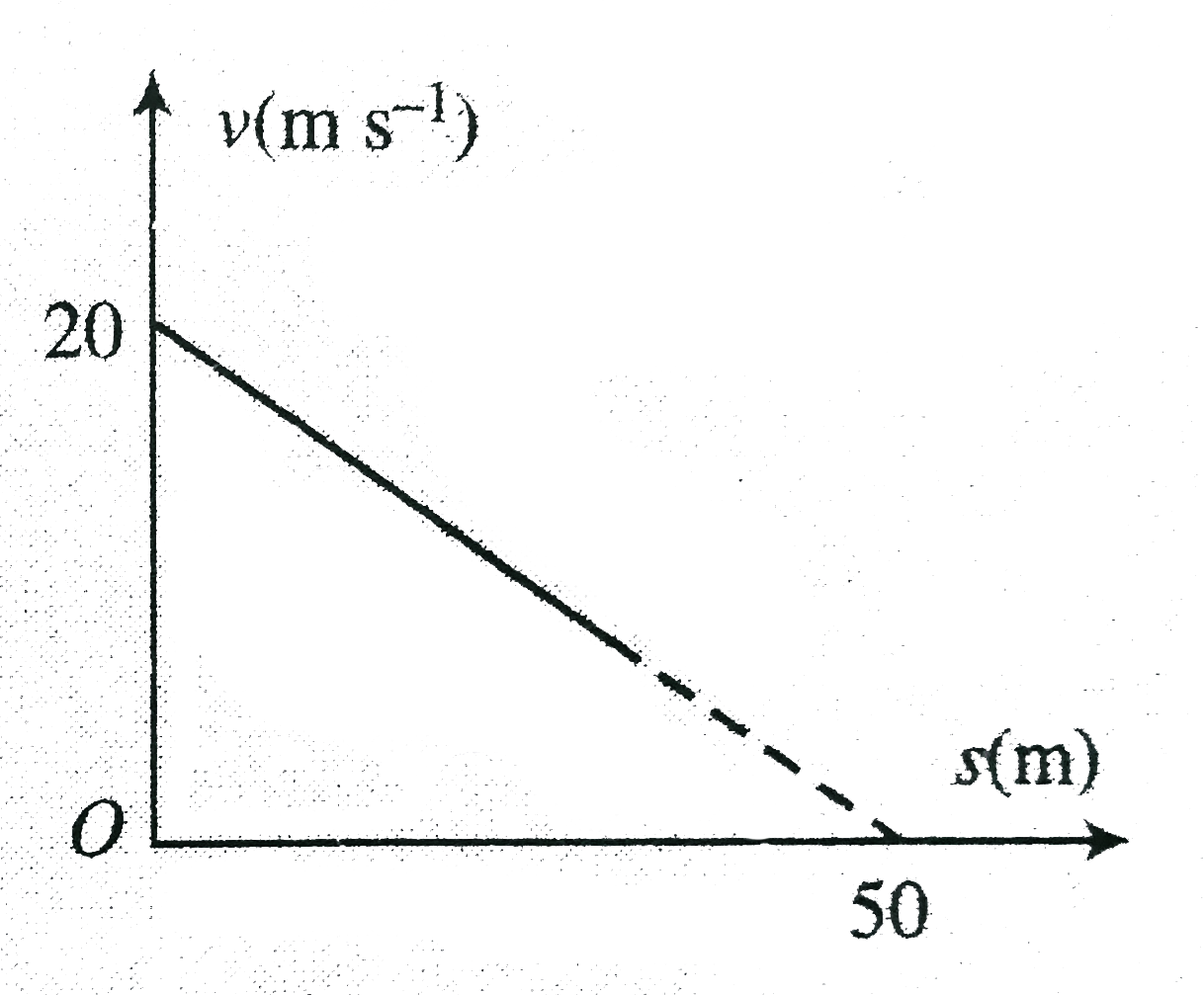 .
.
a. Acceleration of the particle when its velocity becomes half of the initial velocity.
b. Total distance covered by the particle.View SolutionA particle is revolving in a circle of radius 1 m with an angular speed of 12 rad/s. At t = 0, it was subjected to a constant angular acceleration α and its angular speed increased to (480π) rotation per minute (rpm) in 2 sec. Particle then continues to move with attained speed. Calculate
(i) angular acceleration of the particle,
(ii) tangential velocity of the particle as a function of time.
(iii) acceleration of the particle at t = 0.5 second and at t = 3 second
(iv) angular displacement at t = 3 second.View SolutionIf a tangential force mg is applied to a disc of mass m and radius r, the angular acceleration produced in it is?
View SolutionA coin is placed at the edge of a horizontal disc rotating about a vertical axis through its axis with a uniform angular speed 2 rad s−1. The radius of the disc is 50 cm. Find the minimum coefficient of friction between disc and coin so that the coin does not slip. (Take g=10m/s2)
View SolutionIn a non - uniform circular motaion the ratio of tangential to radial acceleration is (where, r= radius of circle, v= speed of the particle, α= angular acceleration)
View SolutionThe radius of gyration of a uniform disc about a line perpendicular to the disc equals to its radius. Find the distance of the line from the centre.
View SolutionA disc initially at rest , is rotated about its axis with uniform angular acceleration . In the first 2 s, it rotates an angle θ . In the next 2s, the disc rotates through an angle
View Solution

