A boat is moving with a velocity 3ˆi+4ˆj with respect to ground. The water in the river is moving with a velocity −3ˆi−4ˆj with respect to ground. The relative velocity of the boat with respect to water is.
8ˆj
−6ˆi−8ˆj
6ˆi+8ˆj
5√2)
The correct Answer is:C
To find the relative velocity of the boat with respect to the water, we can follow these steps:
Step 1: Identify the given velocities
- The velocity of the boat with respect to the ground is given as:
→Vboat=3^i+4^j
- The velocity of the water with respect to the ground is given as:
→Vwater=−3^i−4^j
Step 2: Write the formula for relative velocity
The relative velocity of the boat with respect to the water can be calculated using the formula:
→Vboat, water=→Vboat−→Vwater
Step 3: Substitute the known values into the formula
Substituting the values we identified in Step 1 into the formula from Step 2:
→Vboat, water=(3^i+4^j)−(−3^i−4^j)
Step 4: Simplify the expression
When we subtract the velocity of the water, we need to change the signs:
→Vboat, water=(3^i+4^j)+(3^i+4^j)
This simplifies to:
→Vboat, water=3^i+4^j+3^i+4^j=(3+3)^i+(4+4)^j=6^i+8^j
Step 5: State the final answer
Thus, the relative velocity of the boat with respect to the water is:
→Vboat, water=6^i+8^j
- The velocity of the boat with respect to the ground is given as:
→Vboat=3^i+4^j
- The velocity of the water with respect to the ground is given as:
→Vwater=−3^i−4^j
The relative velocity of the boat with respect to the water can be calculated using the formula:
→Vboat, water=→Vboat−→Vwater
Substituting the values we identified in Step 1 into the formula from Step 2:
→Vboat, water=(3^i+4^j)−(−3^i−4^j)
When we subtract the velocity of the water, we need to change the signs:
→Vboat, water=(3^i+4^j)+(3^i+4^j)
This simplifies to:
→Vboat, water=3^i+4^j+3^i+4^j=(3+3)^i+(4+4)^j=6^i+8^j
Thus, the relative velocity of the boat with respect to the water is:
→Vboat, water=6^i+8^j
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective
40 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A boat stems in a river with velocity 2ˆi+ˆj with respecitve to the ground. The river water flows with a velocity −3ˆi−4ˆj with respect to the ground. What is the relative velocity of boat w.r.t river water ?
View SolutionA plane mirror is moving with velocity 4(ˆi)+4(ˆj)+8(ˆk). A point object in front of the mirror moves with a velocity 3(ˆi)+4(ˆj)+5(ˆk). Here, ˆk is along the normal to the plane mirror and facing towards the object. The velocity of the image is
View SolutionA plane mirror is moving with velocity 4(ˆi)+4(ˆj)+8(ˆk). A point object in front of the mirror moves with a velocity 3(ˆi)+4(ˆj)+5(ˆk). Here, ˆk is along the normal to the plane mirror and facing towards the object. The velocity of the image is
View SolutionRain is falling with a velocity (−4ˆi+8ˆj−10ˆk). A person is moving with a velocity of (6ˆi+8ˆj) on the ground.
Find the velocity of rain with respect to man and the direction from which the rain appears to be coming.
View SolutionIn the figure shown the velocity of A with respect to ground is (20ˆi+15ˆj)m/s, then what will be the magnitude of velocity of the wedge 'B' with respect to ground frame. (A remains in contact with B)
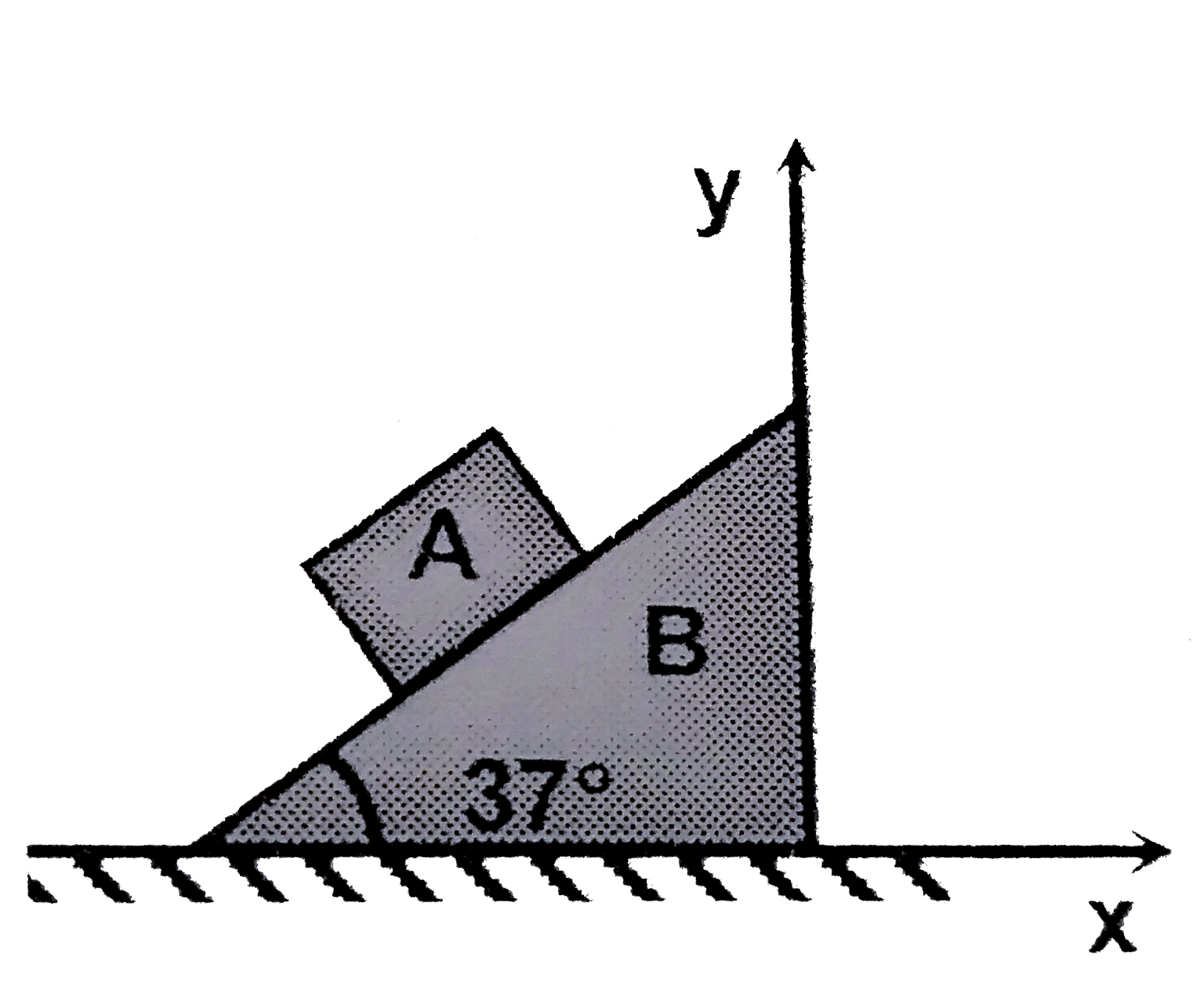
View SolutionRain is falling with a velocity (−4ˆi+8ˆj−10ˆk). A person is moving with a velocity of (6ˆi+8ˆj) on the ground.
The speed with the rain drops hit the person is :
View SolutionA point object is moving with velocity v0=2ˆi−3ˆj+4ˆk in front of a moving plane mirror whose normal is along x - axis.The mirror is moving with velocity vm=ˆi−4ˆj+2ˆk. Find the velocity vector of image
View SolutionA point object infront of a plane mirror has velocity −2ˆi+3ˆj+4ˆk and the mirror has velocity 3ˆi−2ˆj+4ˆk. The x-axis is along the normal of the pane mirrro. Find the velocity of the image.
View SolutionA particle has initial velocity (3ˆi+4ˆj) and has acceleration (0.4ˆi+0.3ˆj). Its speed after 10s is.
View SolutionA particle of mass 'm' moving with a velocity (3ˆi+2ˆj)m/s collides with stationary mass 'M' and finally 'm' moves with a velocity (−2ˆi+ˆj)m/s if mM=113 the velocity of the M after collision is?
View Solution
