A small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
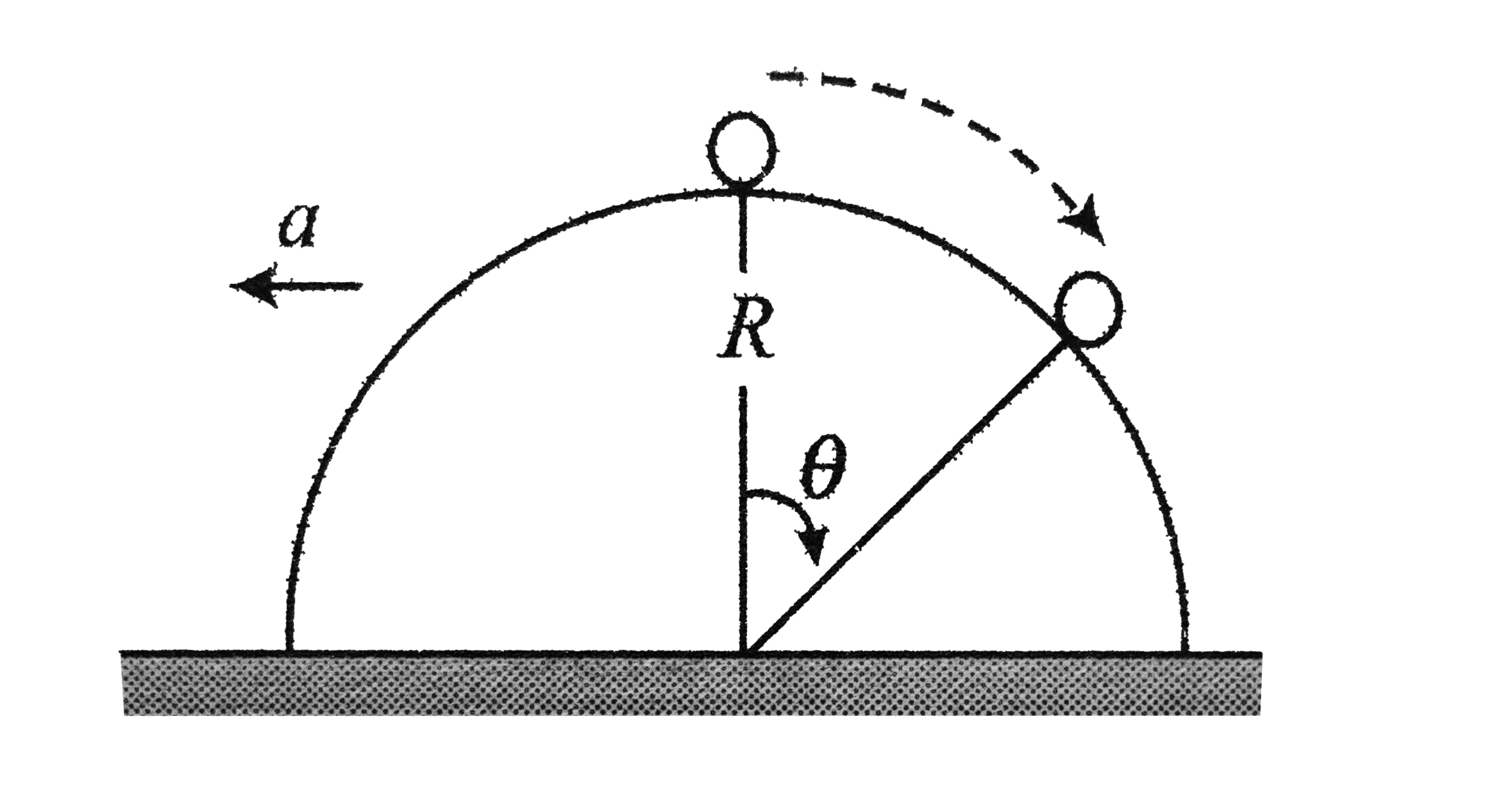
Here we analyze the motion of ball with respect to wedge. As we are analyzing the motion of the ball from accelerating wedge, we impose a pseudo force ma→on the ball.
The work done by the pseudo force is
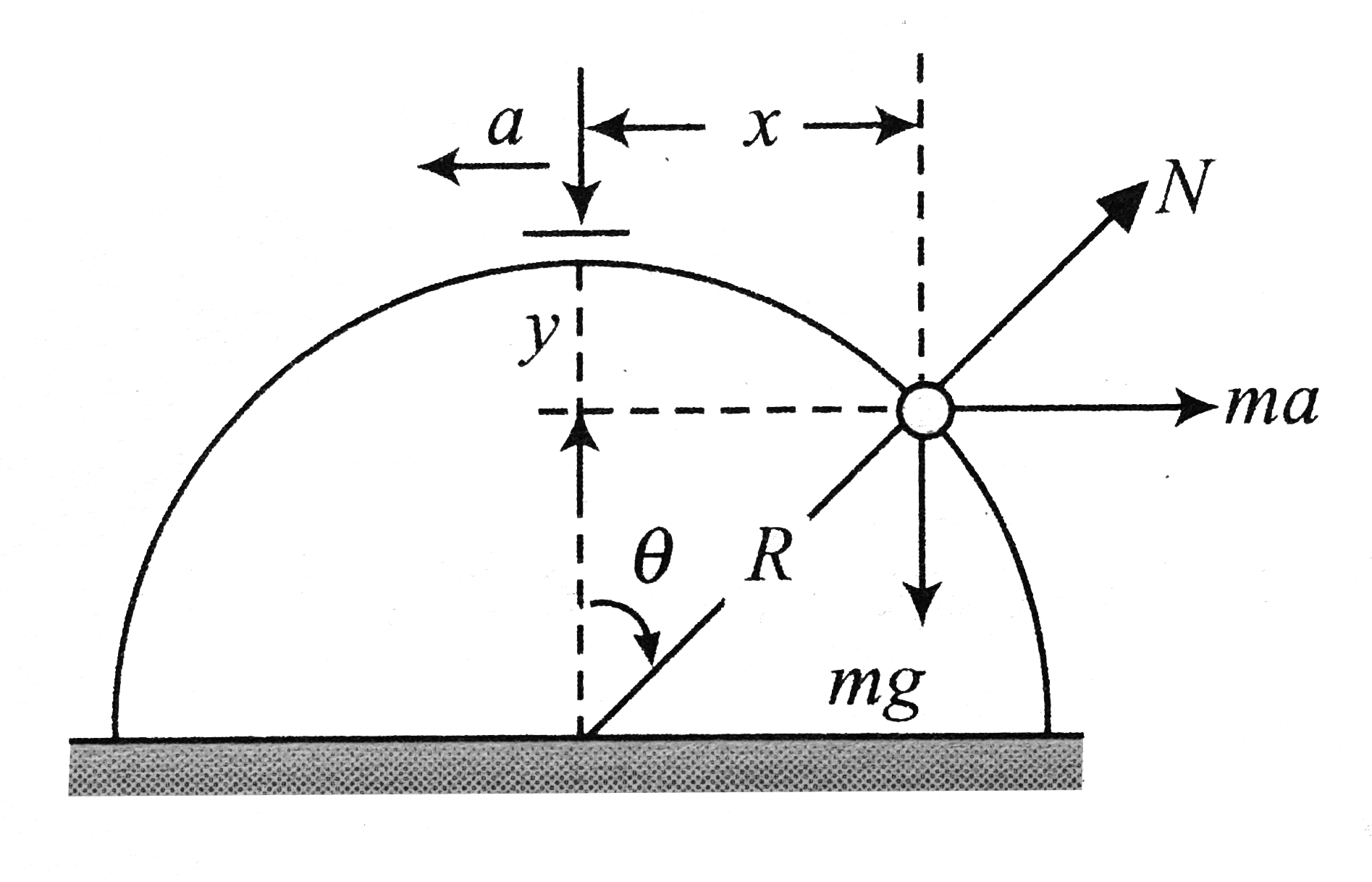
Wps=max
The work done by gravity is Wgr=mgy
The work done by normal reaction force is zero as there is no relative sliding between the ball and the wedge in the direction of normal reaction.
Then, the total work done is
W=max+mgy (i)
KE: The change in kinetic energy of the ball relative to wedge is
K=12mv2 (ii)
where v is the velocity of the ball relative to wedge.
W-E theorem relative to wedge:
W=ΔK (iii)
From Eqs (i), (ii), and (iii), we have
max+mgy=12mv2
Substituting x=Rsinθ and y=R(1−cosθ), we have
v=√2{gR(1−cosθ)+aRsinθ}
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples15videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
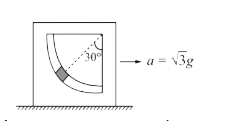
A wedge with a rough groove in the shape of a quarter of a circle is kept on a smooth table (see figure). A small block is placed in the groove with a small clearance. The wedge is moved with an acceleration√3g . If the block is to remain stationary relative to groove in the position shown, the coefficient of friction required can be:
 View Solution
View SolutionFigure shows a block A constrained to slide along the inclined plane of the wedge B shown. Block A is attached with a string which passes through three ideal pulleys and connected to the wedge B. If wedge is pulled toward right with an acceleration a, find
(a) the acceleration of the block with respect to wedge
(b) the acceleration of the block with respect to ground.
 View Solution
View SolutionA block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
 View Solution
View SolutionAll surfaces are smooth in following figure. Find F, such that block remain stationary with respect to wedge.
 View Solution
View SolutionA small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. If h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
View SolutionA block of mass 2kg released from the top of a smooth fixed wedge inside the elevator which is moving downward with an acceleration a = 5 m/s^2 as shown in the figure.The value of acceleration of the block w.r.t wedge will be (g = 10 m/s^2)
View SolutionAll surface are smooth. Find the acceleration of mass m relative to wedge when wedge is moving with acceleration 'a'
 View Solution
View SolutionAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
 View Solution
View SolutionIn fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
 View Solution
View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
 View Solution
View Solution

