The bobo of a pendulum at rest is given a sharp hit to impart a horizontal velocity u where l is the length of the pendulum. Find the angle rotated by the string before it becomes slack.
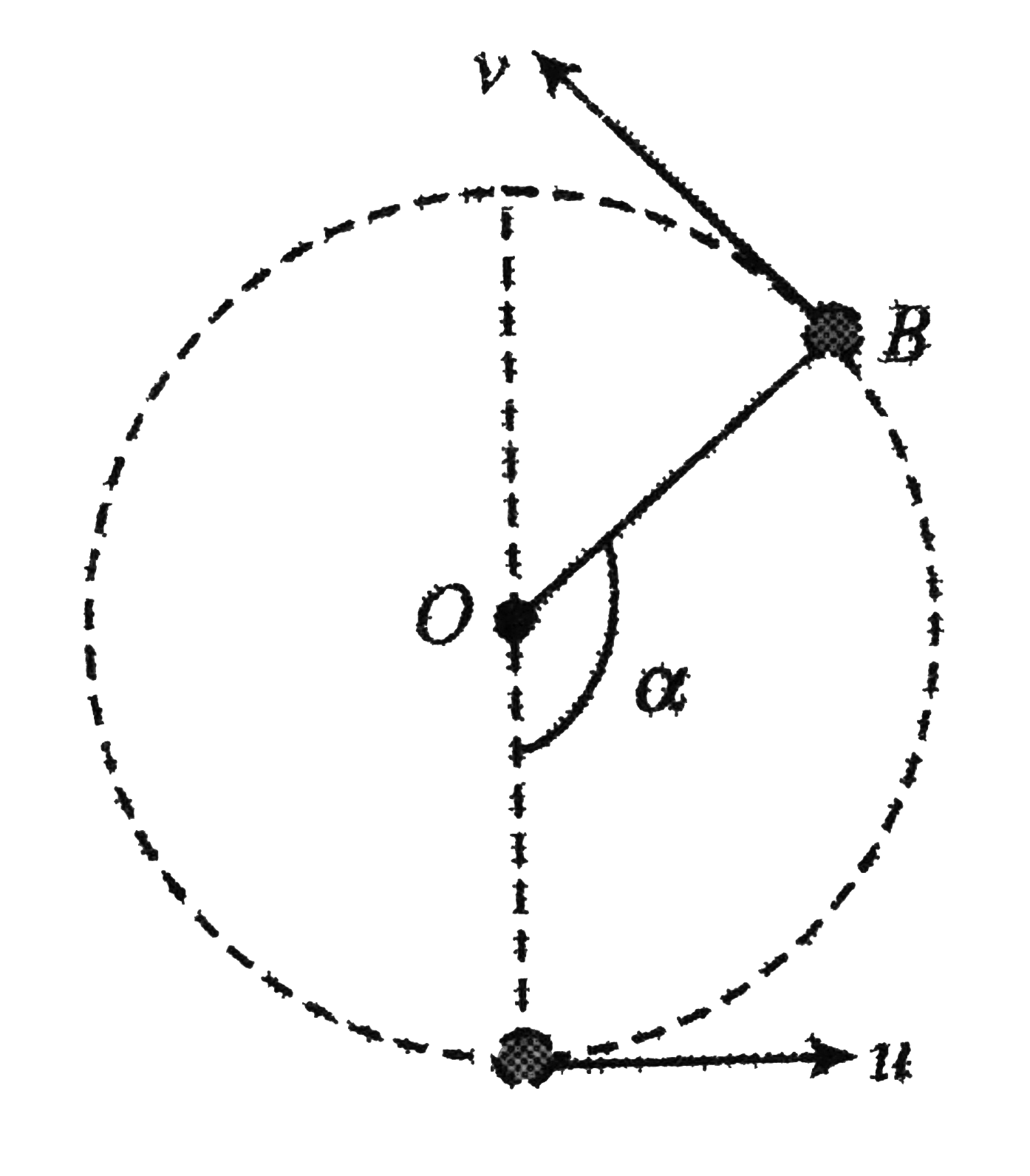
Let stirng slacks at B.
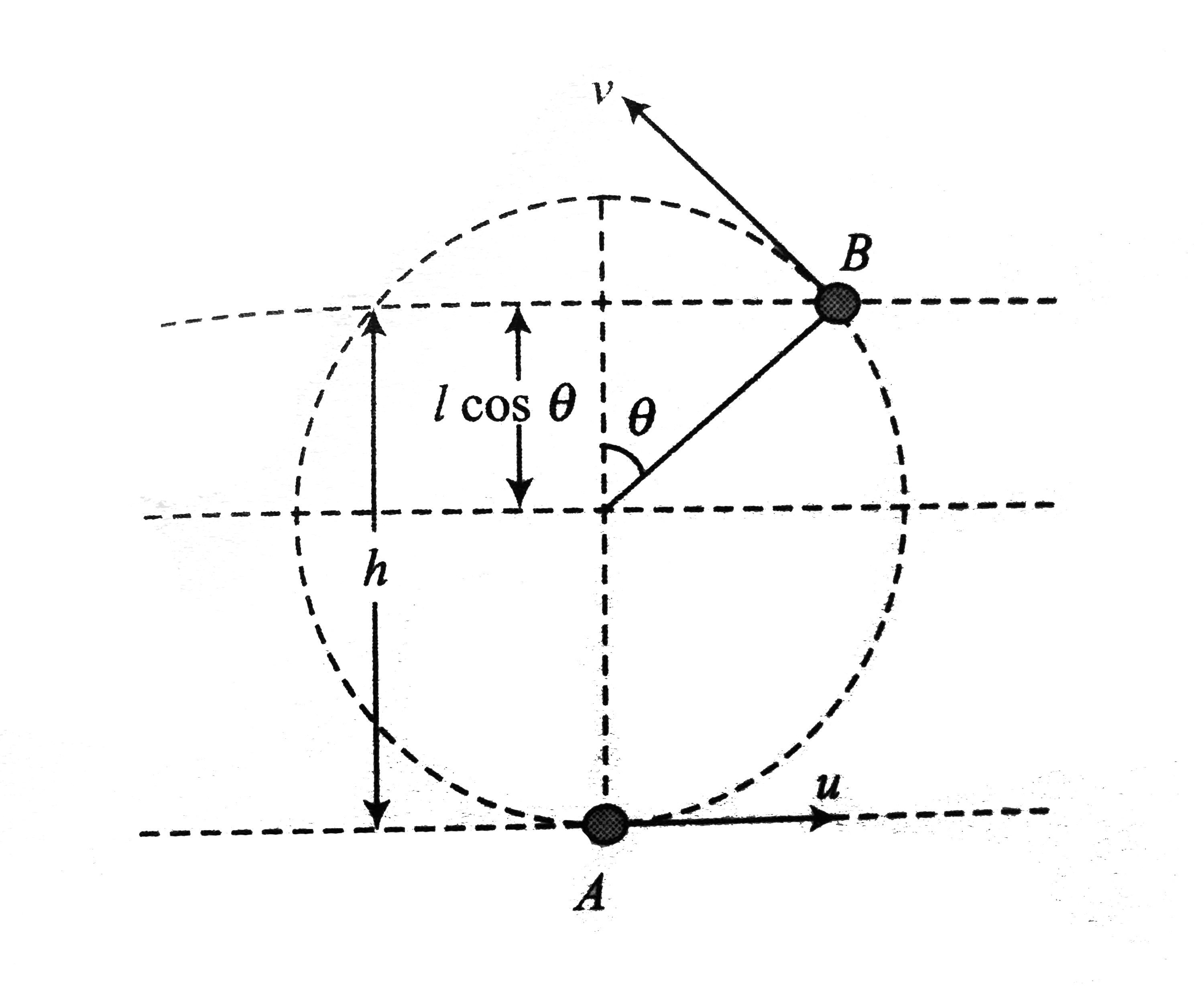
Applying COM, E at A and B, ΔU+ΔK=0
mgh+[12mv2−12μ2]=0
12mv2−12μ2=−mgh
v2=u2−2g(1+1cosθ)
When string slacks tension in the string becomes zero. The component of the weight in radial direction provide centripetal force at this position. From FBD of bob, we can write
mv2l=mgcosθ
v2=lgcosθ (ii)
From equation (i) and (ii), we get
3gl−2glcosθ=glcosθ
3cosθ=1⇒θ=cos−1(13)

Hence, the angle rotated by the string before it becomes slack is
⇒α=π−θ=π−cos−1(13)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples15videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
The bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with the upward vertical.
View SolutionThe bob of a stationary pendulum is given a sharp hit to impart it a horizontal speed of √3gl. Find the angle rotated by the string before it becomes slack.
View Solution
Knowledge Check
- Question 1 - Select One
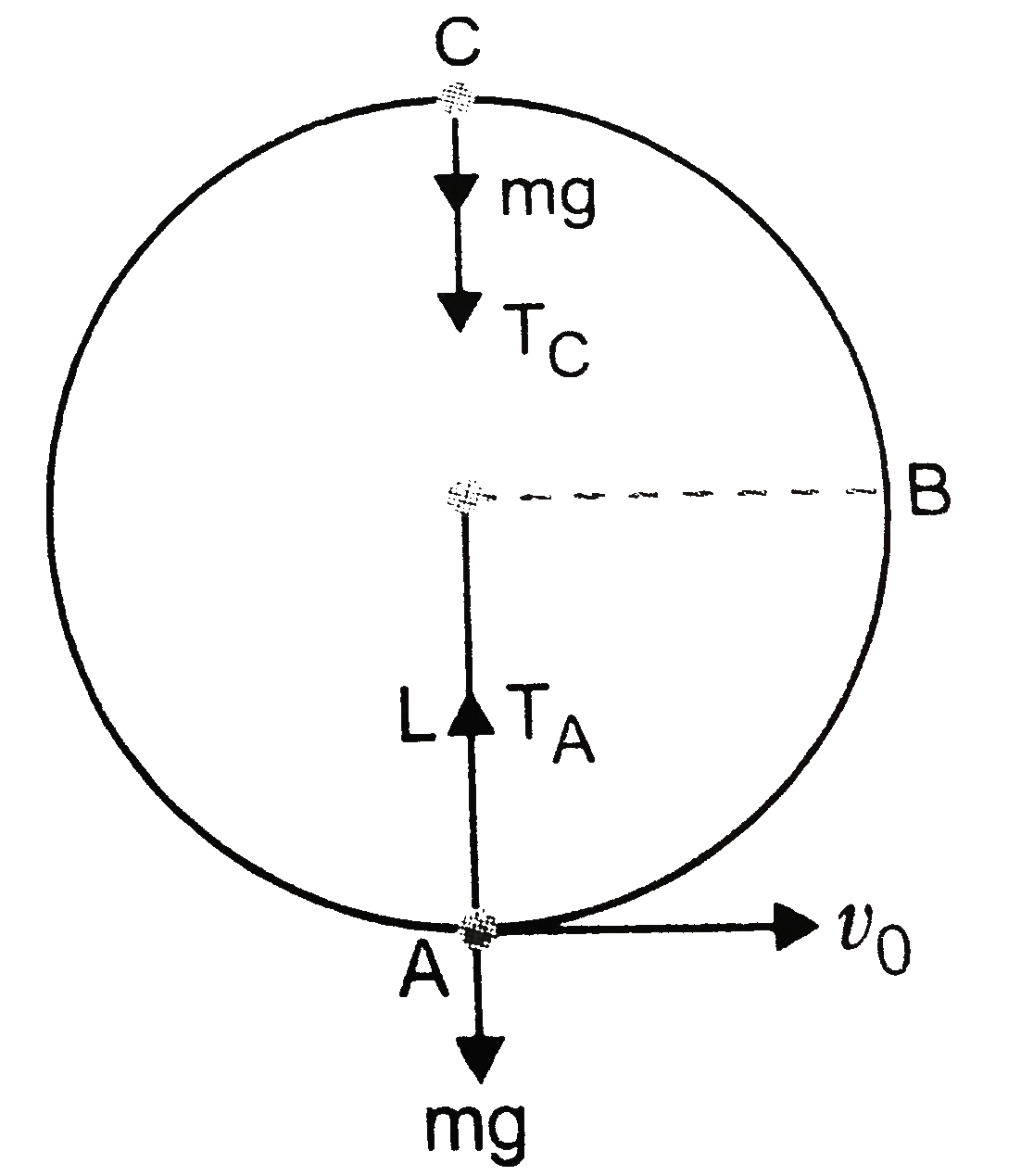
A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
 AA-p,B-q,C-s,D-rBA-q,B-r,C-q,D-sCA-r,B-s,C-q,D-pDA-s,B-p,C-r,D-q
AA-p,B-q,C-s,D-rBA-q,B-r,C-q,D-sCA-r,B-s,C-q,D-pDA-s,B-p,C-r,D-q
The bob of pendulum is project with horizontal velocity of √3gf I is the length of string. Find the angular displacement of string before it becomes slack.
 View Solution
View SolutionA particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.
 View Solution
View SolutionA simple pendulum is suspended from the ceiling a car accelerating uniformly on a horizontal road. If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. A sufficient horizontal velocity =√3gl is imparted to it suddenly. Calculate the angle made by the string with the vertical when the accekleration of the particle is inclined to the string by 45∘ .
View SolutionA block of mass m is attached to a pulley disc of equal mass, radius r by means of a slack string as shown. The pulley is hinged about its centre on a horizontal table and the block is projected with an initial velocity of 5m/s. Find the velocity when the string becomes taut.
 .View Solution
.View SolutionA heavy particle hangs from a point O, by a string of length a. It is projected horizontally with a velocity u=√(2+√3)ag . The angle with the downward vertical, string makes where string becomes slack is :
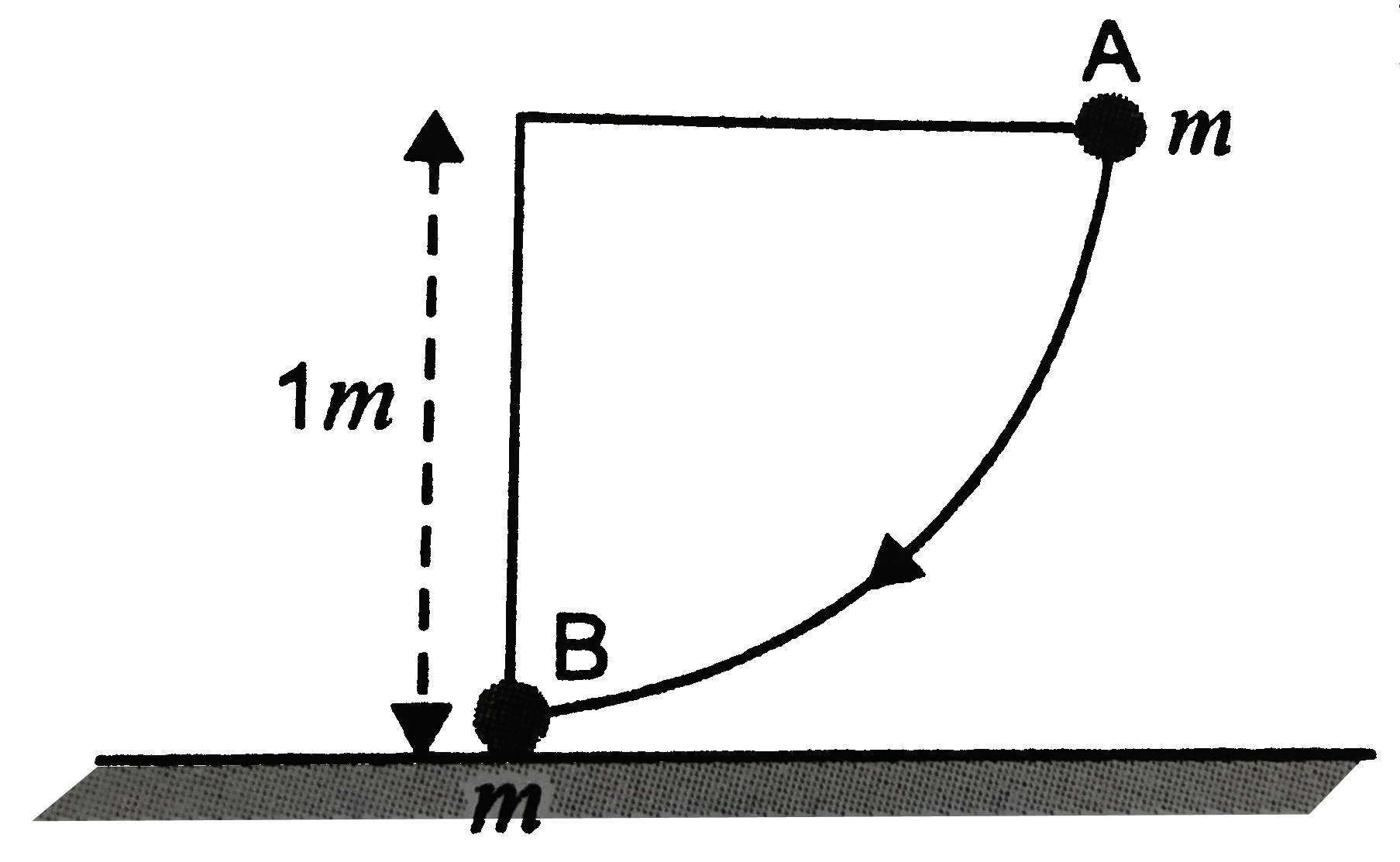
View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
 View Solution
View Solution

