A force F acts on a body such that it is always at an angle of 45∘ to the direction of motion. The body moves in a circle and covers a semicircle of radius R. What is the work done by the force F?
To solve the problem, we need to calculate the work done by a force F acting at an angle of 45∘ to the direction of motion of a body moving along a semicircular path of radius R.
1. Identify the Path and Displacement:
The body moves along a semicircle from point A to point B. The total distance covered along the semicircle is given by:
S=πR
where R is the radius of the semicircle.
Hint: Remember that the distance along a semicircle can be calculated using the formula for the circumference of a circle.
2. Determine the Angle:
The force F acts at an angle of 45∘ to the direction of motion. This means that the angle θ between the force and the displacement is 45∘.
Hint: The angle given in the problem is crucial for calculating the component of the force that does work.
3. Calculate the Work Done:
The work done W by the force can be calculated using the formula:
W=F⋅S⋅cos(θ)
Substituting the values we have:
W=F⋅(πR)⋅cos(45∘)
4. Evaluate cos(45∘):
We know that:
cos(45∘)=1√2
Therefore, substituting this into the work done equation gives:
W=F⋅(πR)⋅1√2
5. Final Expression for Work Done:
Thus, the work done by the force F is:
W=F⋅πR√2
Final Answer:
The work done by the force F while the body moves along the semicircle is:
W=F⋅πR√2
The body moves along a semicircle from point A to point B. The total distance covered along the semicircle is given by:
S=πR
where R is the radius of the semicircle.
The force F acts at an angle of 45∘ to the direction of motion. This means that the angle θ between the force and the displacement is 45∘.
The work done W by the force can be calculated using the formula:
W=F⋅S⋅cos(θ)
Substituting the values we have:
W=F⋅(πR)⋅cos(45∘)
We know that:
cos(45∘)=1√2
Therefore, substituting this into the work done equation gives:
W=F⋅(πR)⋅1√2
Thus, the work done by the force F is:
W=F⋅πR√2
The work done by the force F while the body moves along the semicircle is:
W=F⋅πR√2
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A Force F acts on a body and displaces it by a distance S in direction at an angle θ with the direction of force ,(a) Write the expression for the work done by the force,(b)What should be the angle between the force and displacement so that the work done is (i)zero ,(ii)Maximum ?
View SolutionA force acts on a body and displaces it by a distance S in a direction at an angle with the direction of force. What should be the value of 0 to get the maximum positive work ?
View Solution
Knowledge Check
A force F acting on an object varies with distance x
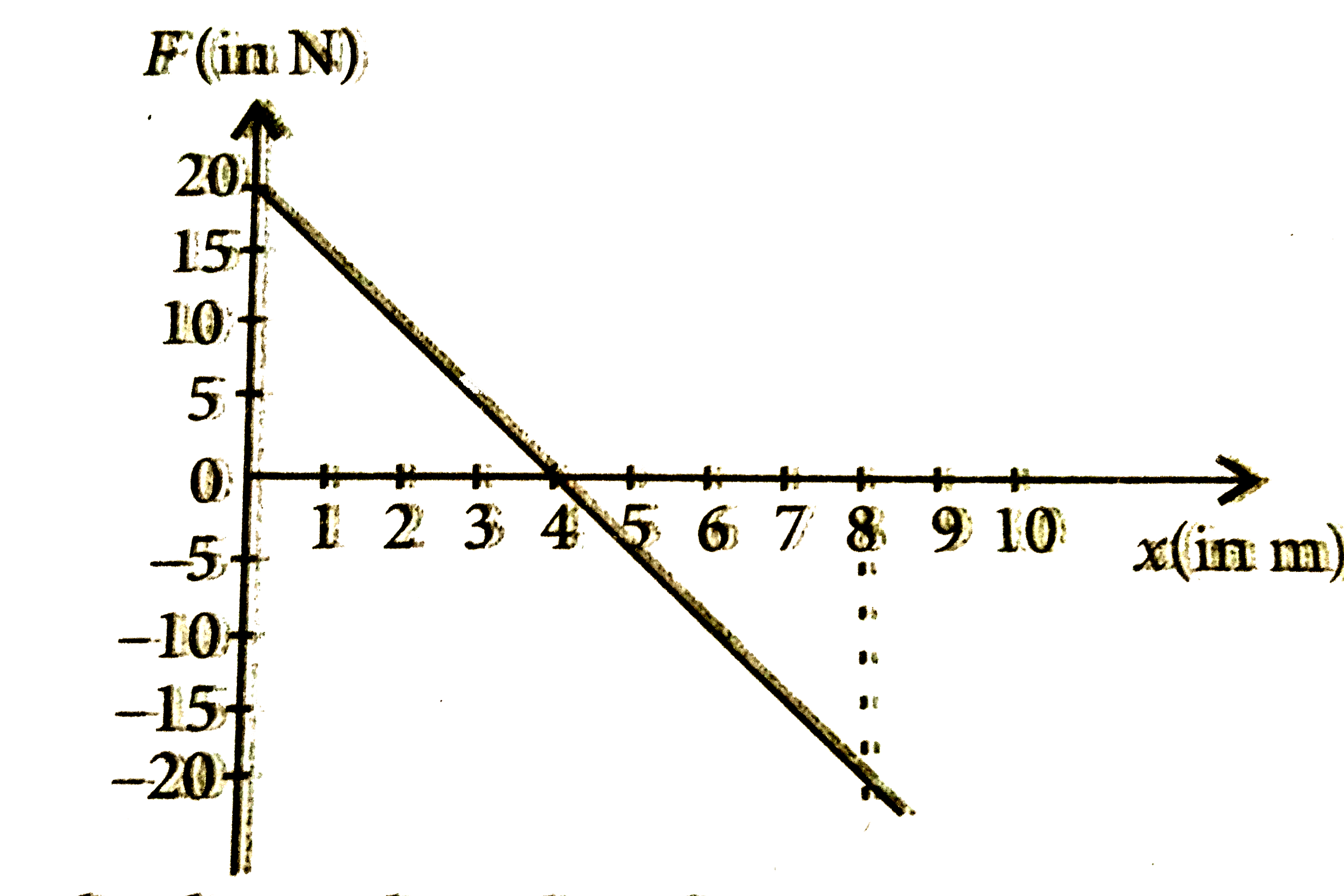
The work done by the force in moving the object from x=0 to x=8 m isAzeroB80 JC−40JD40J
The velocity of a body moving in a straight line is increased by applying a constant force F, for some distance in the direction of the motion. Prove that the increase in the kinetic energy of the body is equal to the work done by the force on the body.
View SolutionA force F=Ay2+By+C acts on a body at rest in the Y-direction. The kinetic energy of the body during a displacement y=−a to y=a is
View SolutionA force F is acted on a body as shown in the figure. Find the impulse of the force in first four seconds.

View SolutionA body is moved in a direction opposite to the direction of force acting on it.State whether the work is done by the work in done against the force.
View SolutionThe force acting on a body is inversely proportional to the distance (x) covered. The work done is proportional to
View SolutionA force F is exerted on a body of mass M, which is connected to a spring (spring constant k). The body has a constant acceleration a. Calculate the work done by the external force in moving the body by a distance D.
View SolutionA body of mass 10 kg is moving on a horizonal surface be applying a force of 10 N in the forward direction. The body moves with a constant velocity of 0.2ms−1. Work done by the force of friction in the first 10 seconds is
View Solution
