In the above question, the average power delivered by gravity is
(a) −mgucosα
(b) −mgusinα
(c) −mgucosα2
(d) −mgusinα2
The correct Answer is:D
To find the average power delivered by gravity when a particle of mass m is projected at an angle α to the horizontal with an initial velocity u, we can follow these steps:
1. Understand the Concept of Average Power:
The average power P delivered by gravity is defined as the total work done by gravity divided by the total time taken to do that work.
P=Wt
2. Calculate the Work Done by Gravity:
The work done by gravity W when the particle reaches its maximum height h is given by:
W=−mgh
where h is the maximum height reached by the particle.
3. Determine the Maximum Height:
The maximum height h can be calculated using the formula:
h=u2sin2α2g
4. Substitute the Maximum Height into the Work Done:
Substitute h into the work done equation:
W=−mg(u2sin2α2g)=−mu2sin2α2
5. Calculate the Time Taken to Reach Maximum Height:
The time t taken to reach the maximum height is given by:
t=usinαg
6. Substitute Work Done and Time into the Average Power Formula:
Now substitute W and t into the average power formula:
P=−mu2sin2α2usinαg
7. Simplify the Expression:
Simplifying the above expression:
P=−mu2sin2α2⋅gusinα=−mgusinα2
8. Final Result:
The average power delivered by gravity is:
P=−mgusinα2
The average power P delivered by gravity is defined as the total work done by gravity divided by the total time taken to do that work.
P=Wt
The work done by gravity W when the particle reaches its maximum height h is given by:
W=−mgh
where h is the maximum height reached by the particle.
The maximum height h can be calculated using the formula:
h=u2sin2α2g
Substitute h into the work done equation:
W=−mg(u2sin2α2g)=−mu2sin2α2
The time t taken to reach the maximum height is given by:
t=usinαg
Now substitute W and t into the average power formula:
P=−mu2sin2α2usinαg
Simplifying the above expression:
P=−mu2sin2α2⋅gusinα=−mgusinα2
The average power delivered by gravity is:
P=−mgusinα2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension55videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective23videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Define average power.
View Solution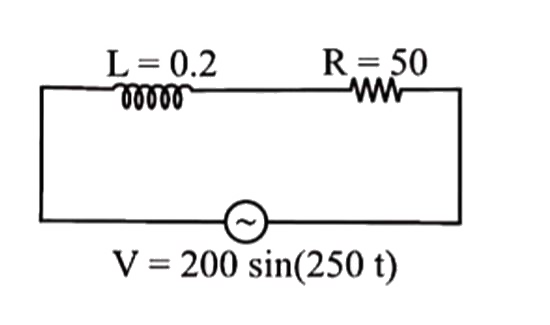
In the given circuit the average power developed is:View SolutionA body is thrown with a velocity v0 at an angle θ0 with horizontal. Find the (a) instantaneous power delivered by gravity after a time t measured from the instant of projection and (b) average power delivered by gravity during the time t.
View SolutionIn the above question, the acceleration of the rim will be?
View SolutionIn the above question, the magnification is
View SolutionA particle is projected with a speed v at an angle θ with the horizontal. Find the mean power delivered by gravity during the ascent of the particle.
View SolutionIn the above question, the angular velocity will:
View SolutionA body of mass m is projected from ground with speed u at an angle θ with horizontal. The power delivered by gravity to it at half of maximum height from ground is
View SolutionAn insect of mass m moves up along a hanging stationary thread, with acceleration a. Find the power delivered by the gravity after a time t.
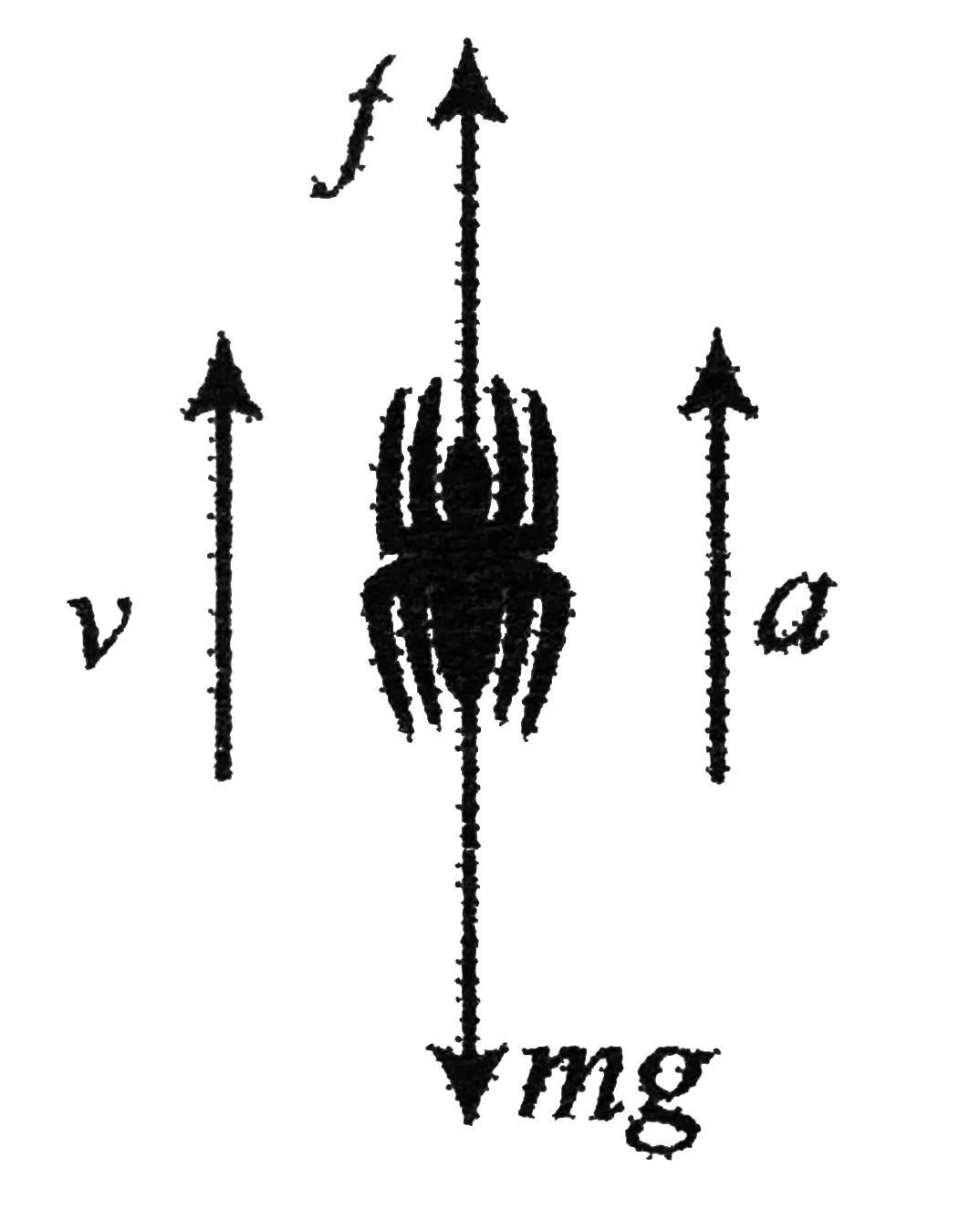 View Solution
View SolutionIn an L−C−R ereis circuit R=150Ω,L=0.0750H and C=0.0180μF . The source has voltage amplitude V=150V and a frequencey equal to the resonacne frequency of the circuit.
(a) What is the power factor ?
(b) What is the average power delivered by the source?
(c) The capacitor is replaced by one with C=0.0360μF and the source frequency is adjusted to the new resonance value. Then, what is the average power delivered by the source?View Solution

