One of the forces acting on the particle is conservative, then
(a) Its work is zero when the particle moves exactly once around any closed path.
(b) Its work equals the change in the kinetic energy of the particle.
(c) It does not obey Newton's second law.
(d) Its work depends on the end points of the motion, not on the path in between.
The correct Answer is:A, D
To solve the question regarding the properties of a conservative force acting on a particle, we can analyze each option provided.
1. Understanding Conservative Forces:
A conservative force is defined as a force for which the work done in moving an object between two points is independent of the path taken. The work done by a conservative force in a closed path is always zero.
2. Analyzing Option A:
The statement is that the work done by a conservative force is zero when the particle moves once around any closed path.
- Conclusion: This is true because, by definition, the work done by a conservative force over a closed loop is zero.
- Result: Option A is correct.
3. Analyzing Option B:
The statement claims that the work done is equal to the change in kinetic energy of the particle.
- Conclusion: While the work-energy theorem states that the total work done on a particle is equal to its change in kinetic energy, this is not specific to conservative forces. Non-conservative forces can also do work that changes kinetic energy.
- Result: Option B is incorrect.
4. Analyzing Option C:
The statement suggests that a conservative force does not obey Newton's second law.
- Conclusion: This is false. Conservative forces can and do obey Newton's second law.
- Result: Option C is incorrect.
5. Analyzing Option D:
The statement indicates that the work done by the force depends only on the endpoints of the motion and not on the path taken.
- Conclusion: This is the defining characteristic of conservative forces. The work done by a conservative force is indeed dependent only on the initial and final positions, not the path taken.
- Result: Option D is correct.
Final Answer:
The correct options are A and D.
A conservative force is defined as a force for which the work done in moving an object between two points is independent of the path taken. The work done by a conservative force in a closed path is always zero.
The statement is that the work done by a conservative force is zero when the particle moves once around any closed path.
- Conclusion: This is true because, by definition, the work done by a conservative force over a closed loop is zero.
- Result: Option A is correct.
The statement claims that the work done is equal to the change in kinetic energy of the particle.
- Conclusion: While the work-energy theorem states that the total work done on a particle is equal to its change in kinetic energy, this is not specific to conservative forces. Non-conservative forces can also do work that changes kinetic energy.
- Result: Option B is incorrect.
The statement suggests that a conservative force does not obey Newton's second law.
- Conclusion: This is false. Conservative forces can and do obey Newton's second law.
- Result: Option C is incorrect.
The statement indicates that the work done by the force depends only on the endpoints of the motion and not on the path taken.
- Conclusion: This is the defining characteristic of conservative forces. The work done by a conservative force is indeed dependent only on the initial and final positions, not the path taken.
- Result: Option D is correct.
The correct options are A and D.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
One of the forces acting on a particle is conservative then which of the following statement (s) are true about this conservative force
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
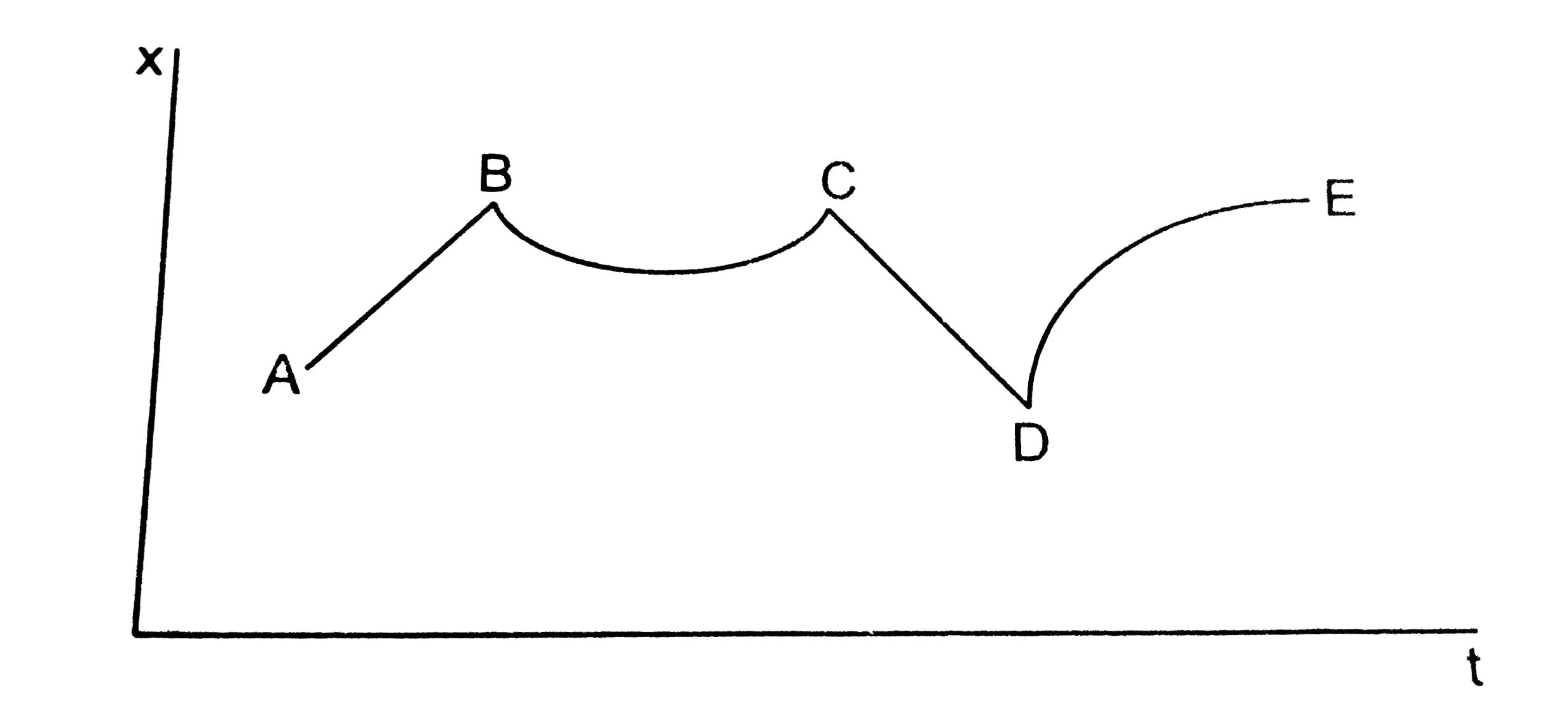
View SolutionA particle is acted upon by only a conservative force F=(7ˆi−6ˆj) N (no other force is acting on the particle). Under the influence of this force particle moves from (0, 0) to (-3m, 4m) then
View SolutionSTATEMENT-1: Work done by the net force acting on a particle is equal to the change in its kinetic energy.
STATEMENT-2: Change in potential energy is always equal to the work done by external forces.
STATEMENT-3: Work energy theorem is not applicable, if the work is done by the non-conservative forces
View SolutionThe momentum of a moving particle given by p=tlnt. Net force acting on this particle is defined by equation F=dpdt. The net force acting on the particle is zero at time
View SolutionA charged is moving with constant velocity parallel to a horizontal current carrying long wire. The direction of velocity of that particle and the current are same. If the force acting on the particle are only magnetic force due to wire and gravitational force due to earth, then the particle :
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
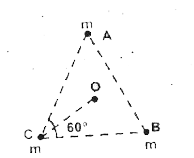
Force acting on particle C, due to particle A and B
View SolutionStatement 1: A charged particle undergoes non-rectilinear motion in a constant magnetic field. The only force acting on the particle is the magnetic force. Then kinetic energy of this particle remains constant but momentum of the particle does not remains constant.
Statement 2: A force that always acts on the particle in direction perpendicular to its velocity does no work on the particle. But whenever a force acts on the particle, momentum of the particle does not remains constant.
View SolutionAssertion Centripetel force (mv2)/(R) acts on a particle rotating in a circle.
Reason Summation of net force acting on the particle is equal to (mv2)/(R) in the above case.
View SolutionIf the resultant of all the external forces acting on a system of particles is zero. Then from an inertial frame, one can surely say that
View Solution
