A ball is thrown upwards into air with a speed greater than its terminal speed. It lands at the same place from where it was thrown. Mark the correct statement (s).
a. It acquires terminal speed before it gets to the highest point of the trajectory.
b. Before reaching the highest point of trajectory, its speed is continuously decreasing.
c. During the entire flight, the force of air resistance is greatest just after it is down
d. The magnitude of net force experienced by the ball is maximum just after it is thrown.
The correct Answer is:B, C, D
To solve the problem, we need to analyze the motion of a ball thrown upwards with a speed greater than its terminal speed and determine which statements about its motion are correct.
1. Understanding Terminal Speed:
- Terminal speed is the constant speed that a freely falling object eventually reaches when the resistance of the medium (air resistance) prevents further acceleration. When the ball is thrown upwards with a speed greater than its terminal speed, it will initially accelerate upwards.
2. Forces Acting on the Ball:
- When the ball is thrown upwards, two forces act on it:
- Gravitational force (mg) acting downwards.
- Air resistance (F_a) acting upwards, which is proportional to the velocity of the ball (F_a = k * v).
- Initially, the ball has a large upward velocity, so the air resistance is also large, but it is still less than the gravitational force.
3. Motion Upwards:
- As the ball moves upwards, its velocity decreases due to the net force acting downwards (mg + F_a). The speed of the ball continuously decreases until it reaches the highest point, where its velocity becomes zero.
4. At the Highest Point:
- At the highest point, the velocity of the ball is zero. Therefore, it cannot have acquired terminal speed before reaching this point because terminal speed is a constant speed that occurs when the forces are balanced (when the net force is zero).
5. Motion Downwards:
- After reaching the highest point, the ball starts descending. During this phase, the gravitational force (mg) acts downwards, and the air resistance (F_a) acts upwards. The ball will accelerate downwards until it reaches terminal speed, where the forces balance out.
6. Analyzing the Statements:
- Statement A: "It acquires terminal speed before it gets to the highest point of the trajectory."
- Incorrect: The ball cannot acquire terminal speed before reaching the highest point because at that point, its velocity is zero.
- Statement B: "Before reaching the highest point of the trajectory, its speed continuously decreases."
- Correct: The speed decreases as the ball moves upwards due to the net downward force.
- Statement C: "During the entire flight, the force of air resistance is greatest just after it is thrown."
- Correct: The air resistance is proportional to velocity, which is maximum just after the ball is thrown.
- Statement D: "The magnitude of the net force experienced by the ball is maximum just after it is thrown."
- Correct: The net force is maximum just after the throw because the gravitational force is at its maximum and the air resistance is also significant at that moment.
Conclusion:
The correct statements are:
- Statement B
- Statement C
- Statement D
- Terminal speed is the constant speed that a freely falling object eventually reaches when the resistance of the medium (air resistance) prevents further acceleration. When the ball is thrown upwards with a speed greater than its terminal speed, it will initially accelerate upwards.
- When the ball is thrown upwards, two forces act on it:
- Gravitational force (mg) acting downwards.
- Air resistance (F_a) acting upwards, which is proportional to the velocity of the ball (F_a = k * v).
- Initially, the ball has a large upward velocity, so the air resistance is also large, but it is still less than the gravitational force.
- As the ball moves upwards, its velocity decreases due to the net force acting downwards (mg + F_a). The speed of the ball continuously decreases until it reaches the highest point, where its velocity becomes zero.
- At the highest point, the velocity of the ball is zero. Therefore, it cannot have acquired terminal speed before reaching this point because terminal speed is a constant speed that occurs when the forces are balanced (when the net force is zero).
- After reaching the highest point, the ball starts descending. During this phase, the gravitational force (mg) acts downwards, and the air resistance (F_a) acts upwards. The ball will accelerate downwards until it reaches terminal speed, where the forces balance out.
- Statement A: "It acquires terminal speed before it gets to the highest point of the trajectory."
- Incorrect: The ball cannot acquire terminal speed before reaching the highest point because at that point, its velocity is zero.
- Statement B: "Before reaching the highest point of the trajectory, its speed continuously decreases."
- Correct: The speed decreases as the ball moves upwards due to the net downward force.
- Statement C: "During the entire flight, the force of air resistance is greatest just after it is thrown."
- Correct: The air resistance is proportional to velocity, which is maximum just after the ball is thrown.
- Statement D: "The magnitude of the net force experienced by the ball is maximum just after it is thrown."
- Correct: The net force is maximum just after the throw because the gravitational force is at its maximum and the air resistance is also significant at that moment.
The correct statements are:
- Statement B
- Statement C
- Statement D
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type35videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Integer Type17videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
Similar Questions
Knowledge Check
- Question 1 - Select One
A ball A is thrown up vertically with a speed u and at the same instant another ball B is released from a height h. At time t, the speed A relative to B is
AuBu - 2gtC√u2−2ghDu - gt
A ball of mass 1kg is thrown up with an initial speed of 4m/s. A second ball of mass 2kg is released from rest from some height as shown in Fig. Choose the correct statement (s).
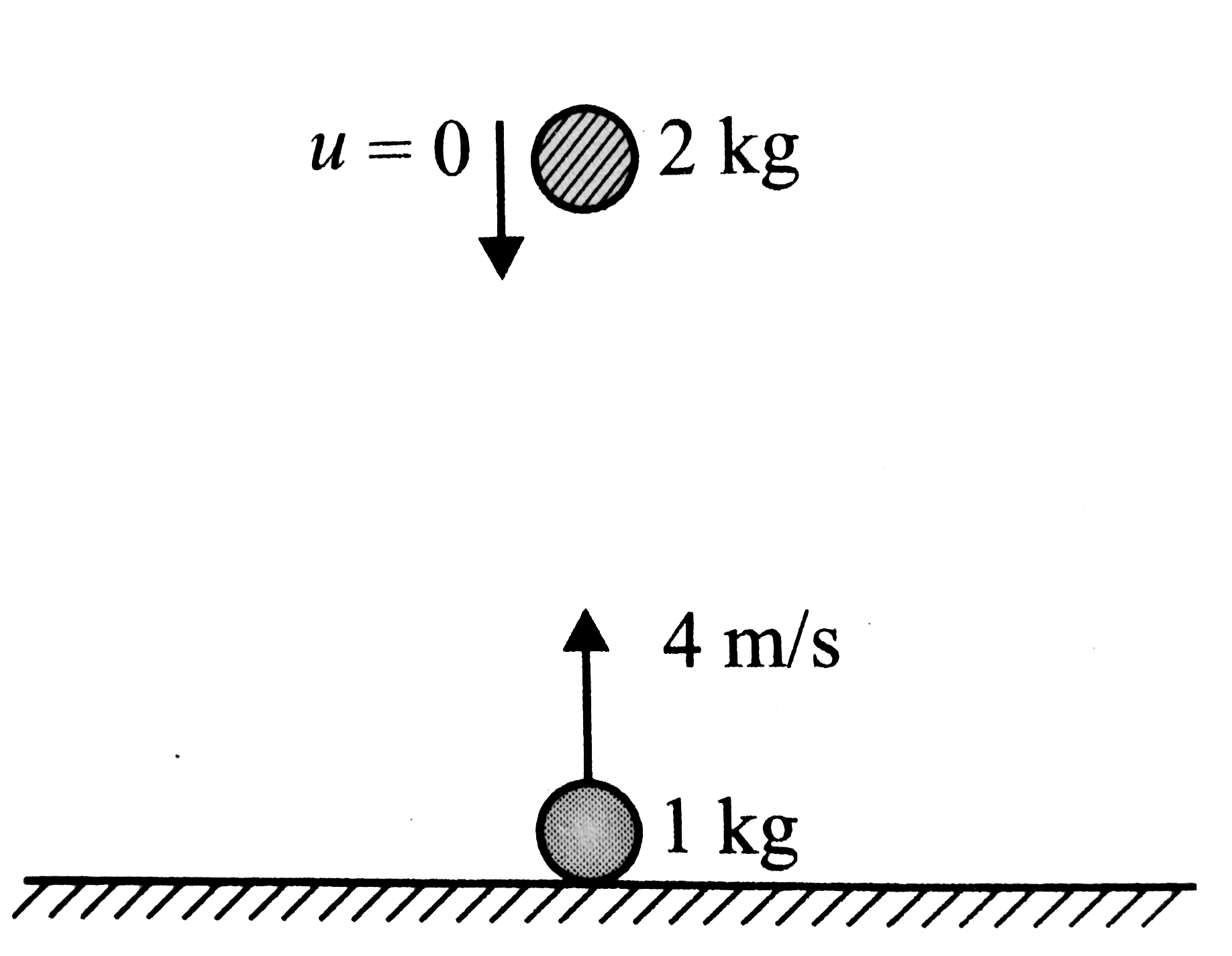 View Solution
View SolutionA ball is thrown upwards, it takes 4 s to reach back to the ground. Find its initial velocity
View SolutionA ball is thrown onto a smooth floor with speed u at angle θ=45∘. If it rebounds with a speed v at the same angle ϕ=45∘. Then the coefficient of restitution is
 View Solution
View SolutionA ball thrown vertically upward returns to its starting point in 4 s. Find its initial speed.
View SolutionIf a ball is thrown vertically upwards with speed u, the distance covered during the last t second of its ascent is
View SolutionA ball is thrown vertically upwards in air, If the resistance cannot be neglected (assume it to be directly proportional to velocity), then choose the correct options. (Assume that resistance force is less than weight of ball and g is acceleration of the ball due to graviy)
View SolutionA ball is thrown from a point with a speed 'v^(0)' at an elevation angle of θ . From the same point and at the same instant , a person starts running with a constant speed 'v0'2 to catch the ball . Will the person be able to catch the ball ? If yes, what should be the angle of projection θ ?
View Solution


