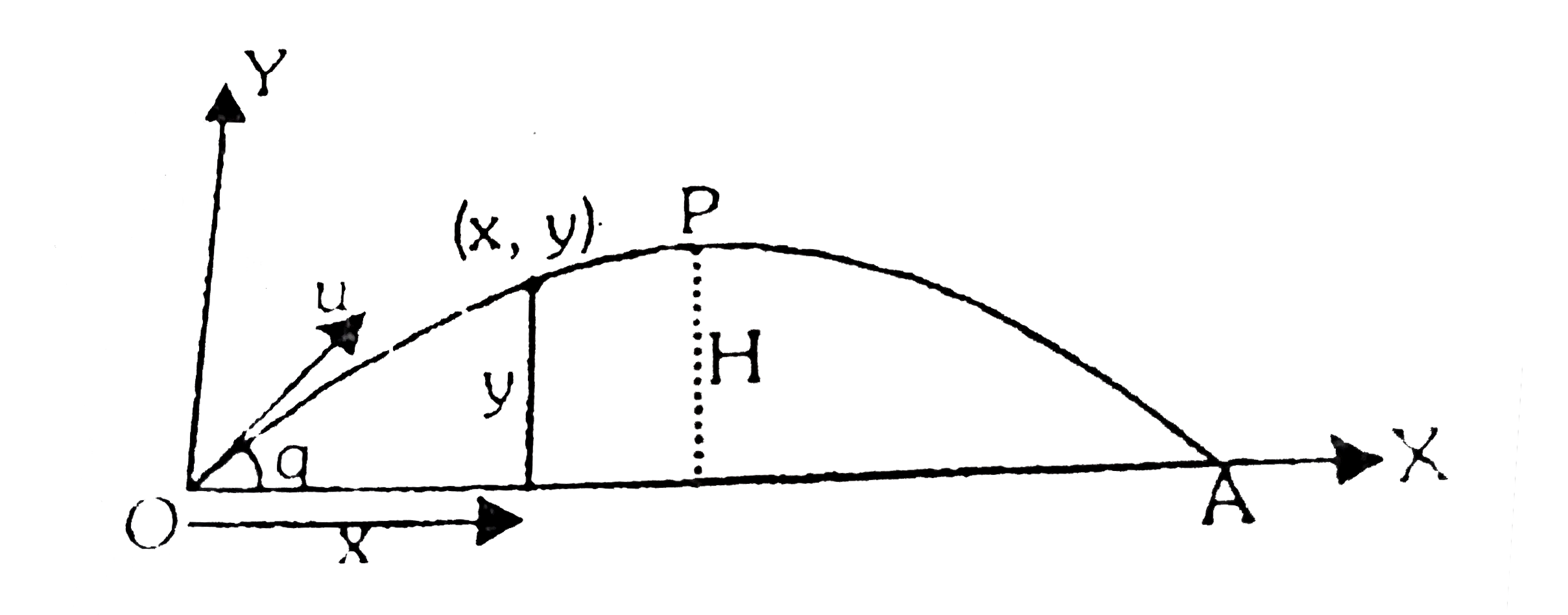The trajectory of a projectile in a vertical plane is y=ax−bx2, where aandb are constant and xandy are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.
The correct Answer is:a24b
Given that y=ax−bx2
Comparing it with equation of a projectile , we get

y=xtanθ−gx22ucos2θ⇒tanθ=a………(i)
and g2bcosθ=b……..(ii)
u2=g2bcos2θ=g(a2+1)2b ........(iii)
[.:cosθ=1√a2+1]
Maximum height attained , H=u2sin2θ2g .......(iv)
From Eq. (ii) , g2b=u2cos2θ
⇒g2b=u2−u2sin2θ
⇒u2sin2θ=u2−g2b
⇒u2sin2θ=g(a2+1)2b−g2b=ga22b ...........(v)
From Eqs. (iv) and (v), H=ga22b×2g=a24b and angle of
projection with horizontal is θ=tan−1(a)
Alternatively:
dydx=a−2bx=0 (For maximum height)
⇒x=a2b
Substituting the value of x∈y=ax−bx2 to find maximum height, H=a(a2b)−b(a24b2)=a22b−a22b=a24b .
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - True or False2videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Integer Type17videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
Similar Questions
Knowledge Check
- Question 1 - Select One
If R and H represent horizontal range and maximum height of the projectile, then the angle of projection with the horizontal is
Atan−1(HR)Btan−1(2HR)Ctan−1(4HR)Dtan−1(4HH) - Question 2 - Select One
The horizontal range of projectile is 4√3 times the maximum height achieved by it, then the angle of projection is
A30∘B45∘C60∘D90∘
The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Angle of projection θ is :-View SolutionA projectile is projected from ground such that the maximum height attained by, it is equal to half the horizontal range.The angle of projection with horizontal would be
View SolutionThe horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Maximum height H is :-View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Time of flight of the projectile is :-View SolutionThe horizontal and vertical displacements x and y of a projectile at a given time t are given by x=6tandy=8t−5t2 meter.The range of the projectile in metre is:
View Solution