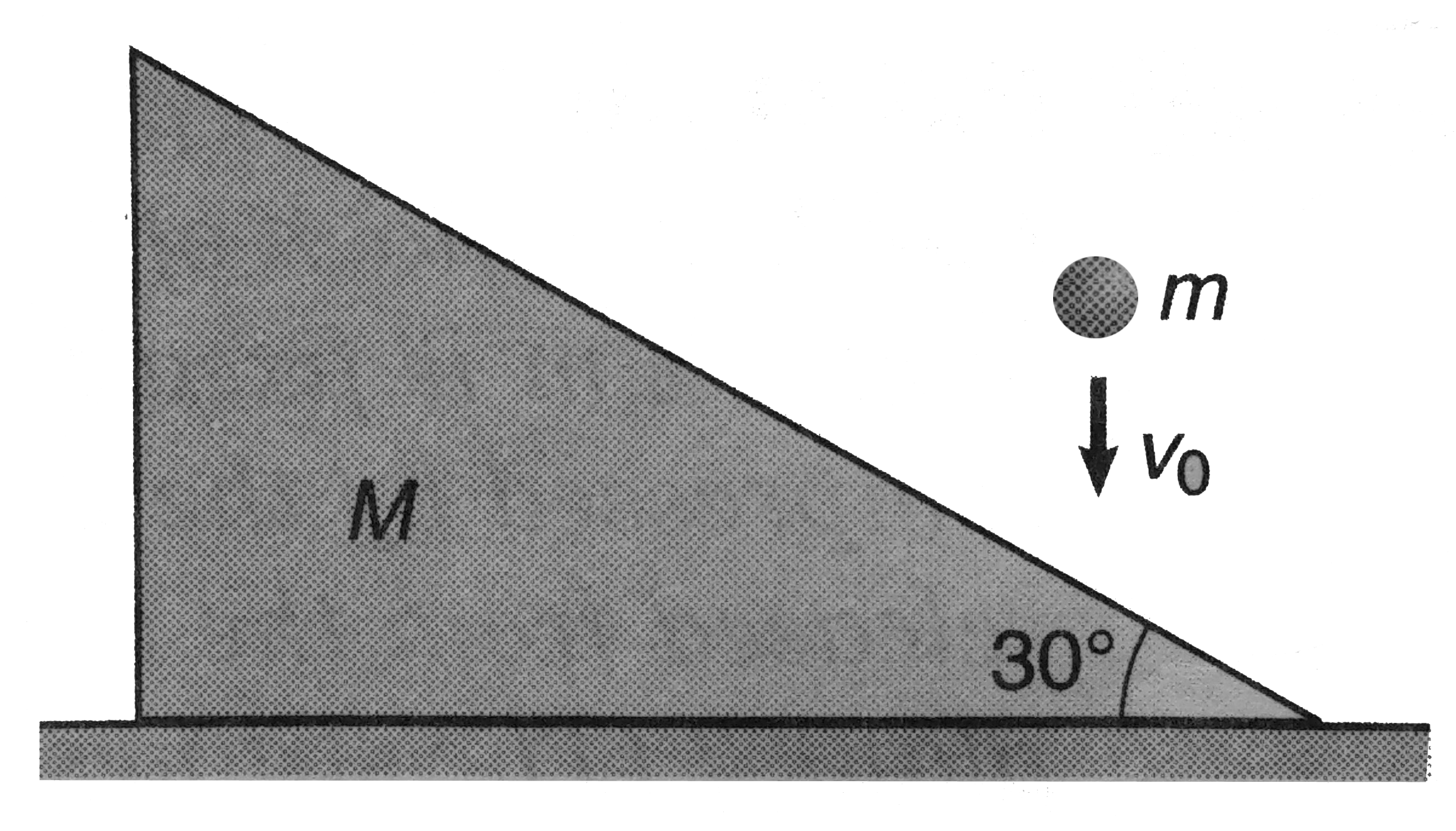
A ball of mass moving horizotally which velocity hits a wedge of mass . The wedge is situated on a smooth horizontal source. If after striking with wedge the ball starts moving in vertical direction and the wedge starts moving in horizotal plane. calculate
a. the velocity of wedge .
b. the velocity at which the ball moves in vertical direction.
c. the impulse imparted by the ball on the wedge.
d. the coefficient of restitution
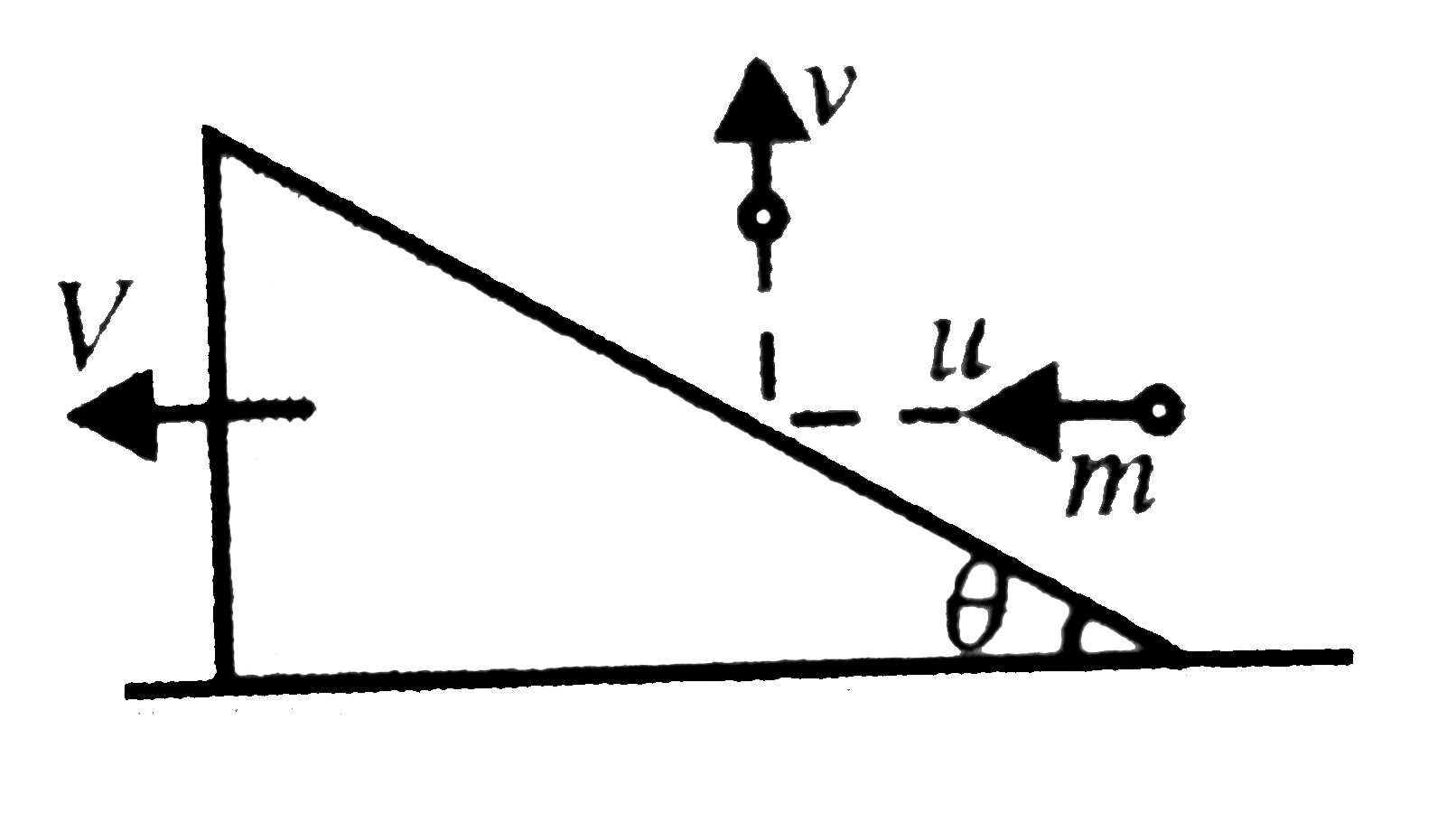
a. As no external force is acting on the system in horizontal direction the linear momentum should be constant and conserved in horizontal direction.
Let velocity of wedge after collision be .
Then ………..i
b. As there is no impulse on the ball in the direction parallel to sloping side hence the veloicty of ball along the slope (tangent direction) should remain unchanged,
..........ii
c. we can find the values of and by impulse approach, when ball hits the wedge the impulse is generated between ball and wedge in the direction perpendicular to slopping surface. (normal direction).

For ball:
from eqn i and ii
From eqn iii
Which gives
d. The direction of restitution is given as

Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

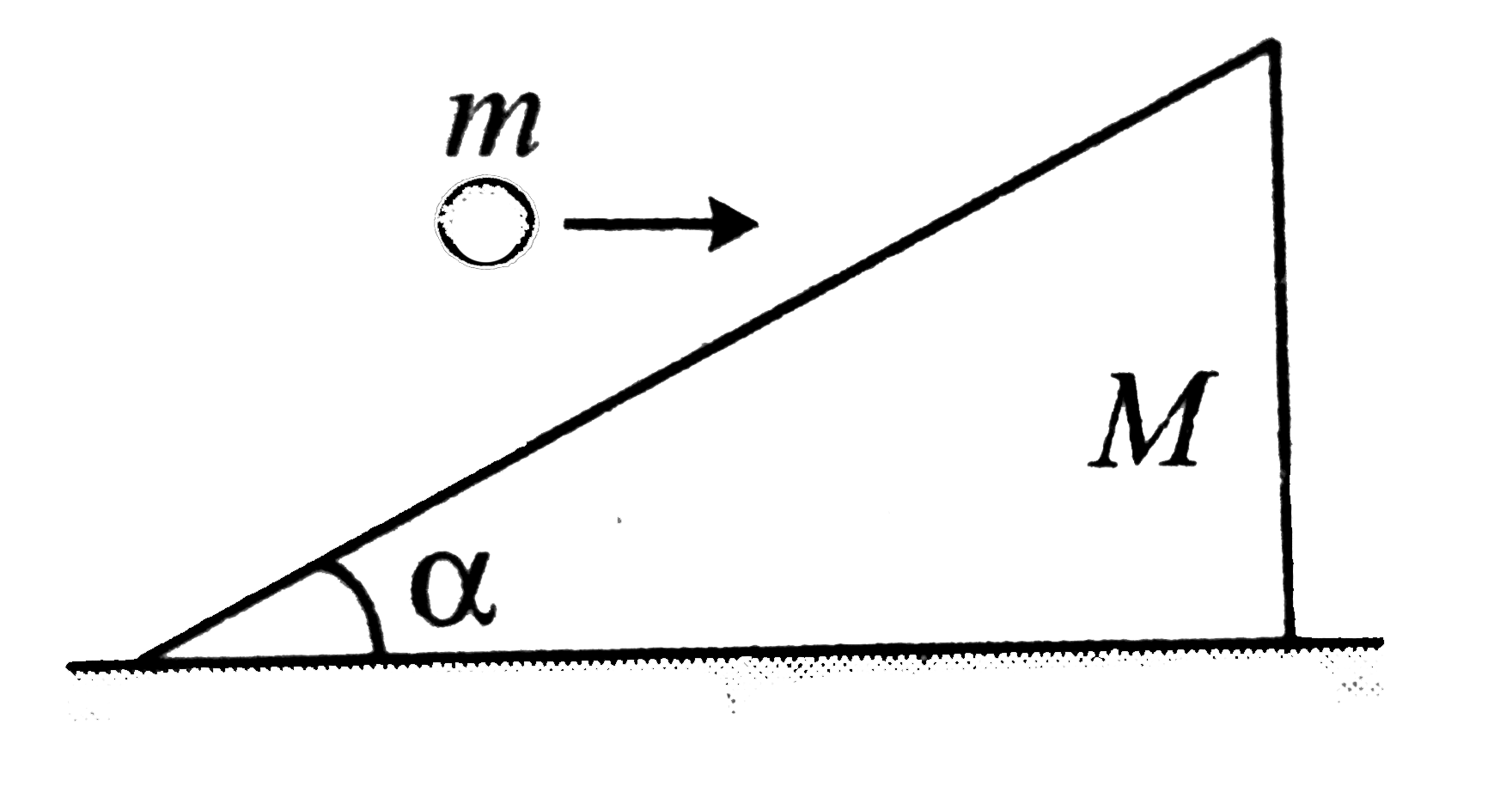
View SolutionA ball of mass m moving with constant horizontal velocity u strikes a stationary wedge of mass M on its inclined surface as shown in the figure. After collision, the ball starts moving up the inclined plane. The wedge is placed on frictionless horizontal surface.
a. Calculate the velocity of wedge immediately after collision.
b. Calculate the maximum height the ball can ascend on the wedge.
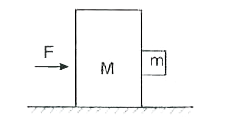
View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
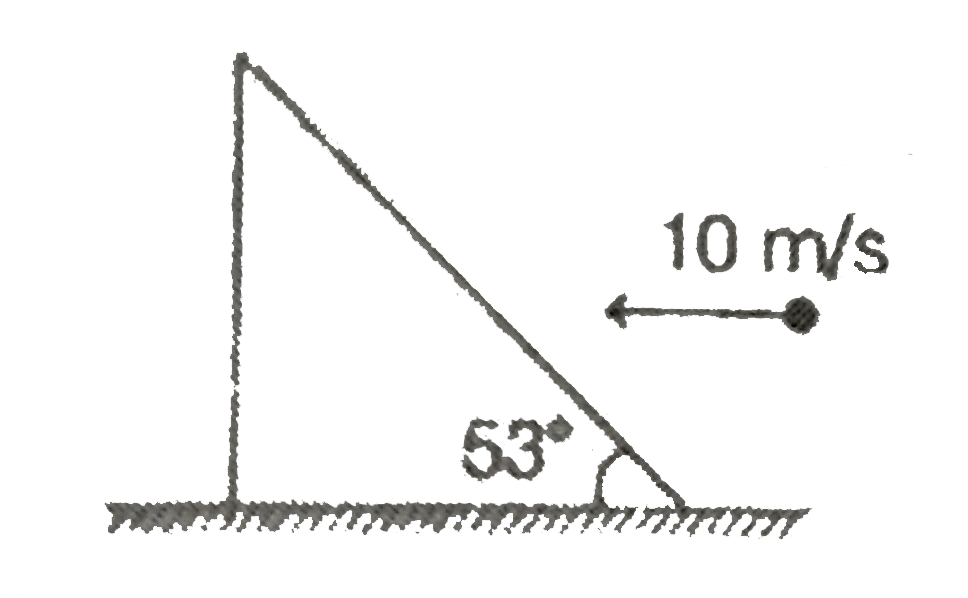
View SolutionA ball mass 2 kg moving horizontally with velocity 10 m/s hits a wedge of mass 5 kg placed on a horizontal surface as shown in the figure. Just after collision klvelocity of wedge is 3.2 m/s. There is no friction at any contact surface. Then (take sin 30∘=3/5)
View SolutionA ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept on a smooth, horizontal surface as shown in figure. If impulse between ball and wedge during collision is J. Then make two equations which relate J with velocity components of wedge and ball. Also find impulse on wedges from ground during impact.
View SolutionA small ball of mass m is projected with a minimum horizontal velocity v0 on a smooth wedge of mass M so that it will reach the highest point of the wedge. Find the value of v0

View SolutionA wedge is placed on a smooth horizontal plain and a rat runs on its sloping side. The velocity of the wedge is v=4ms−1 towards the right. What should be the velocity of the rat with respect to the wedge (u), so that the rat appears to ,move in the vertical direction to an observer stading on the ground?

View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
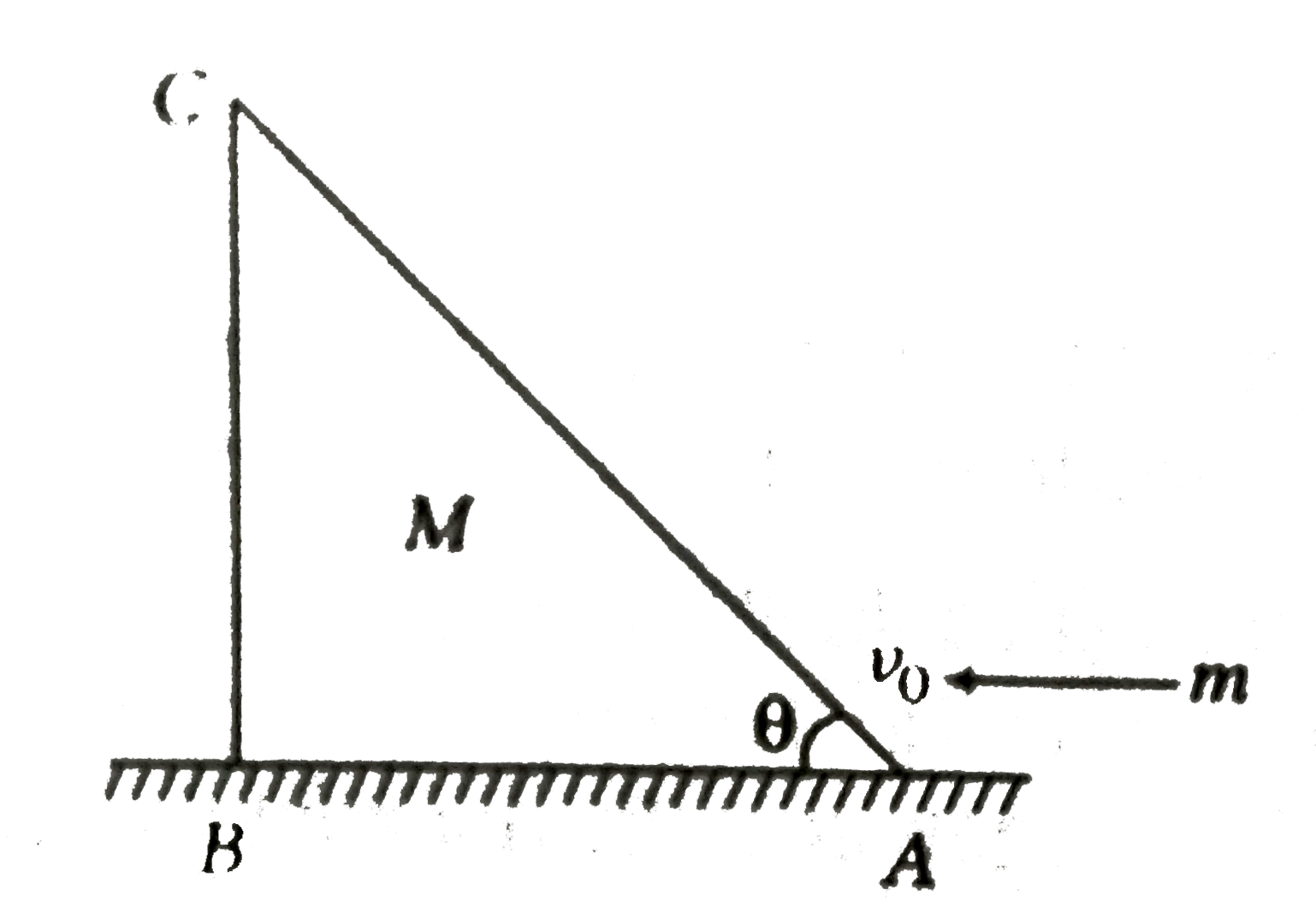
View SolutionA shell of mass m is moving horizontally with velocity v0 and collides with the wedge of mass M just above points A, as shown in the figure. As a consequences, wedge starts to move towards left and the shell returns with a velocity in xy-plance. The principle of conservation of momentum can be applied for
View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View Solution
