The momentum of a moving particle is vectorially given a, where stands for time. Choose the correct option:
The applied force is constant.
The momentum is constant.
The applied force always remains perpendicular to the momentum.
The applied force is always parallel to the momentum.
The correct Answer is:C
To solve the problem, we need to analyze the momentum vector given by:
→p=p0(cost^i+sint^j)
where p0 is a constant and t represents time.
Step 1: Understand the momentum vector
The momentum vector →p is expressed in terms of time t. The components of the momentum in the x and y directions are p0cost and p0sint, respectively.
Step 2: Differentiate momentum to find force
According to Newton's second law, the force →F is the time derivative of momentum:
→F=d→pdt
Step 3: Differentiate each component of momentum
We will differentiate →p:
→F=ddt(p0cost^i+p0sint^j)
Using the chain rule, we differentiate each component:
→F=p0(−sint^i+cost^j)
Step 4: Analyze the force
The force vector is given by:
→F=−p0sint^i+p0cost^j
Since the force depends on t (due to the sine and cosine functions), we conclude that the force is not constant.
Step 5: Check if momentum is constant
Since →p depends on t (as it contains cost and sint), we can conclude that the momentum is also not constant.
Step 6: Check if force is perpendicular to momentum
To check if the force is always perpendicular to the momentum, we need to verify if the dot product of →F and →p is zero:
→F⋅→p=(−p0sint^i+p0cost^j)⋅(p0cost^i+p0sint^j)
Calculating the dot product:
=(−p0sint)(p0cost)+(p0cost)(p0sint)
=−p20sintcost+p20costsint=0
Since the dot product is zero, the force is indeed perpendicular to the momentum.
Conclusion
Based on the analysis:
1. The applied force is not constant.
2. The momentum is not constant.
3. The applied force is always perpendicular to the momentum.
Thus, the correct option is that the applied force always remains perpendicular to the momentum.
The momentum vector →p is expressed in terms of time t. The components of the momentum in the x and y directions are p0cost and p0sint, respectively.
According to Newton's second law, the force →F is the time derivative of momentum:
We will differentiate →p:
The force vector is given by:
Since →p depends on t (as it contains cost and sint), we can conclude that the momentum is also not constant.
To check if the force is always perpendicular to the momentum, we need to verify if the dot product of →F and →p is zero:
=−p20sintcost+p20costsint=0
Based on the analysis:
1. The applied force is not constant.
2. The momentum is not constant.
3. The applied force is always perpendicular to the momentum.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
On the P−T graph of an ideal gas, choose the correct option(s):
View SolutionChoose the correct option w.r.t given figure :
View SolutionThe linear momentum of a particle is given by →P=(asintˆi−acostˆj)kg−m/s. A force →F is acting on the particle. Select correct alternative/s:
View SolutionThe linear momentum of a particle as a fuction of time 't' is given by , p = a +bt , where a and b are positive constants . What is the force acting on the particle ?
View SolutionThe displacement (x) of a particle as a function of time (t) is given by
x=asin(bt+c)
Where a,b and c are constant of motion. Choose the correct statemetns from the following.
View SolutionA particle start from rest, with uniform acceleration at time t, choose the correct option
View SolutionThe momentum of a moving particle given by p=tlnt. Net force acting on this particle is defined by equation F=dpdt. The net force acting on the particle is zero at time
View SolutionThe linear momentum of a particle varies with times as p=a0+at+bt2. What s force and time relation ?
View SolutionA particle is acted upon by a force whose component's variations with time are shown in diagrams. Then choose the correct option(s)
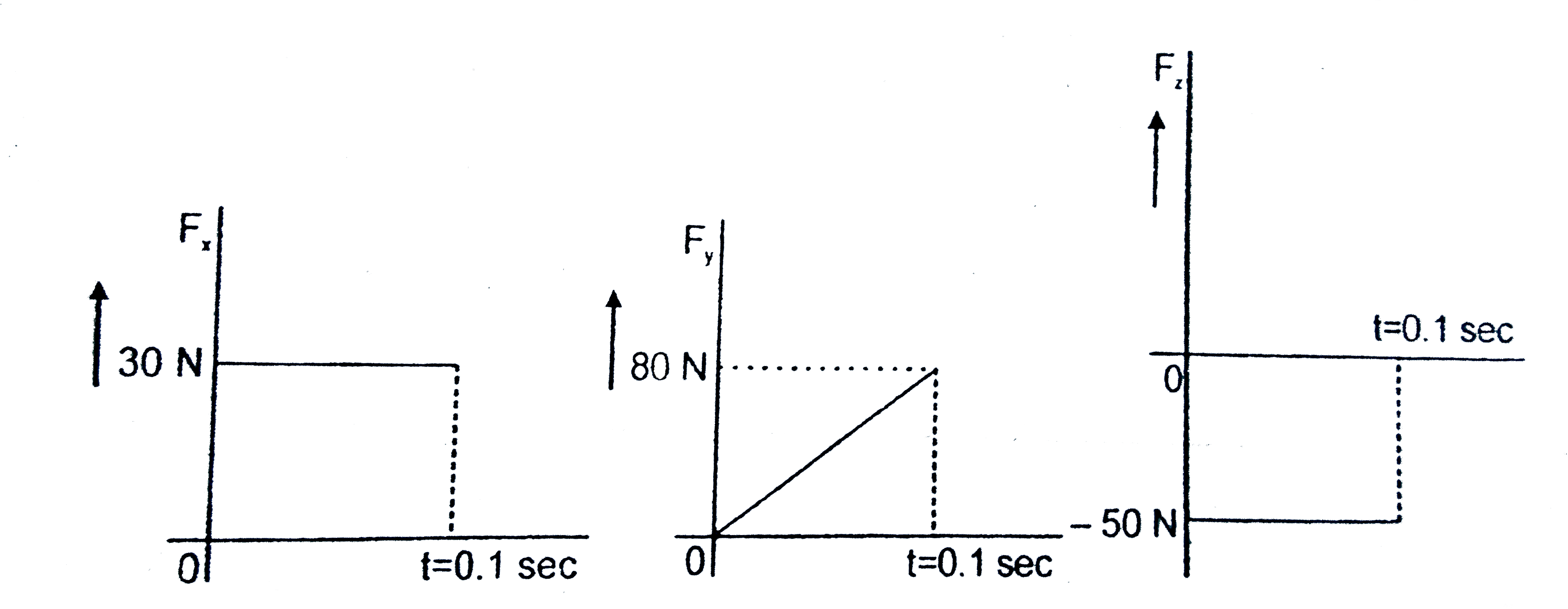
View SolutionThe linear momentum P of a particle varies with time as follows P=a+bt2
Where a and b are constants. The net force acting on the particle is
View Solution
