A pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
If the bob is just able to complete the circular motion, then tension at the lowest point just when the bob starts rising will be
6Mg
5Mg
3Mg
Mg
The correct Answer is:A
To solve the problem step by step, let's break it down:
Step 1: Understand the scenario
A pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v and emerges from the bob with a speed of v2. We need to find the tension in the string at the lowest point of the pendulum's swing when the bob starts rising.
Step 2: Analyze the motion at the top of the swing
For the bob to just complete the circular motion, at the highest point of the swing, the tension T in the string will be zero. The forces acting on the bob at this point are:
- Weight of the bob: Mg
- Centripetal force required to keep the bob in circular motion: Mv21l
Setting the centripetal force equal to the weight:
Mv21l=Mg
This simplifies to:
v21=gl
Step 3: Calculate the velocity of the bob just after the bullet passes through it
Using the principle of conservation of momentum, the momentum before the bullet hits the bob is equal to the momentum after the bullet exits:
mv=(M+m)vb+mv′b
where vb is the velocity of the bob after the bullet enters, and v′b=v2 is the velocity of the bullet after it exits.
Rearranging gives:
mv=Mvb+mv′b
Substituting v′b:
mv=Mvb+m(v2)
mv−mv2=Mvb
mv2=Mvb⟹vb=mv2M
Step 4: Calculate the velocity of the bob at the lowest point
Using conservation of energy between the lowest point and the point just after the bullet exits:
12Mv2b+mgh=12M(0)2+mgh
At the lowest point, the total energy is:
12M(0)2+mgh+12mv′2b
Step 5: Calculate the tension at the lowest point
At the lowest point, the forces acting on the bob are:
- Tension T upwards
- Weight Mg downwards
- Centripetal force Mv2l
Using the equation of motion:
T−Mg=Mv2l
Thus,
T=Mg+Mv2l
Step 6: Substitute the values
We already found that vb=mv2M and v21=gl.
Substituting v2 into the tension equation gives:
T=Mg+M(5gL)l
Final Step: Conclusion
The tension at the lowest point when the bob starts rising is:
T=6Mg
A pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v and emerges from the bob with a speed of v2. We need to find the tension in the string at the lowest point of the pendulum's swing when the bob starts rising.
For the bob to just complete the circular motion, at the highest point of the swing, the tension T in the string will be zero. The forces acting on the bob at this point are:
- Weight of the bob: Mg
- Centripetal force required to keep the bob in circular motion: Mv21l
Mv21l=Mg
This simplifies to:
v21=gl
Using the principle of conservation of momentum, the momentum before the bullet hits the bob is equal to the momentum after the bullet exits:
mv=(M+m)vb+mv′b
where vb is the velocity of the bob after the bullet enters, and v′b=v2 is the velocity of the bullet after it exits.
mv=Mvb+mv′b
Substituting v′b:
mv=Mvb+m(v2)
mv−mv2=Mvb
mv2=Mvb⟹vb=mv2M
Using conservation of energy between the lowest point and the point just after the bullet exits:
12Mv2b+mgh=12M(0)2+mgh
At the lowest point, the total energy is:
12M(0)2+mgh+12mv′2b
At the lowest point, the forces acting on the bob are:
- Tension T upwards
- Weight Mg downwards
- Centripetal force Mv2l
T−Mg=Mv2l
Thus,
T=Mg+Mv2l
We already found that vb=mv2M and v21=gl.
Substituting v2 into the tension equation gives:
T=Mg+M(5gL)l
The tension at the lowest point when the bob starts rising is:
T=6Mg
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
If the bob stops where the string becomes horizontal then v is
View SolutionA pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
What is the momentum transferred to the bob by the bullet?
View Solution
Knowledge Check
A simple pendulum of length 1 m has a wooden bob of mass 1 kg. It is struck by a bullet of mass 10−2 kg moving with a speed of 2×102ms−1. The height to which the bob rises before swinging back is (Take g=10ms−2)
A0.2 mB0.6 mC8 mD1 m
A pendulum consists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed of (v1)/3 and the bob just completes motion along a vertical circle, then v1 is
View SolutionA pendulum consists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed of (v1)/3 and the bob just completes motion along a vertical circle, then v1 is
View SolutionA pendulum comsists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1 and it emerges from the bob with speed v13. The bob just completes motion along a vertical circle. Then v1 is
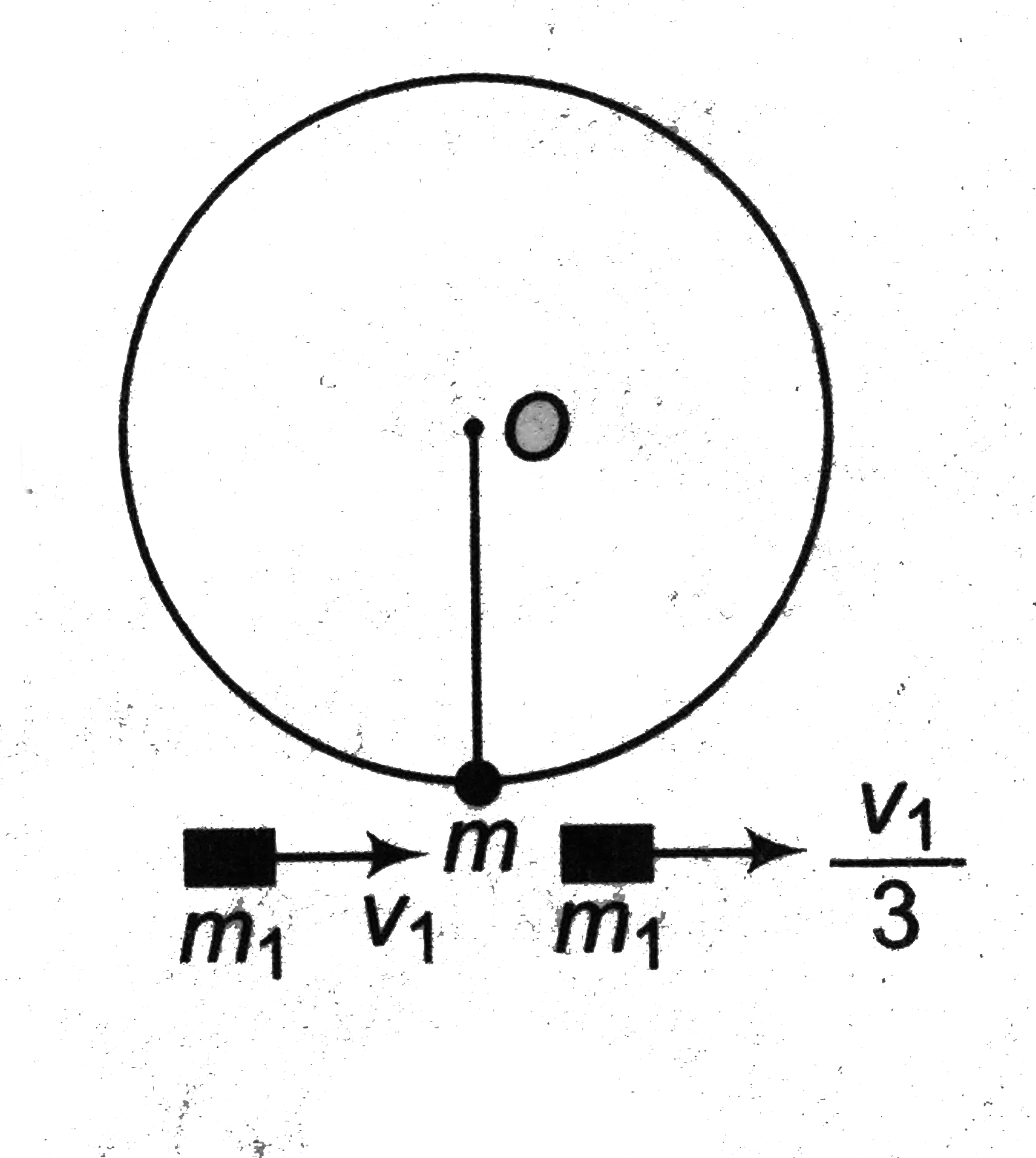
View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionSuppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
View SolutionA bullet of mass 50g if fired from below into the bob of mass 450g of a long simple pendulum as shown in Fig. The bullet remains inside the bob and the bob rises through a height of 1.8m. Find the speed of the bullet.Take g=10ms2
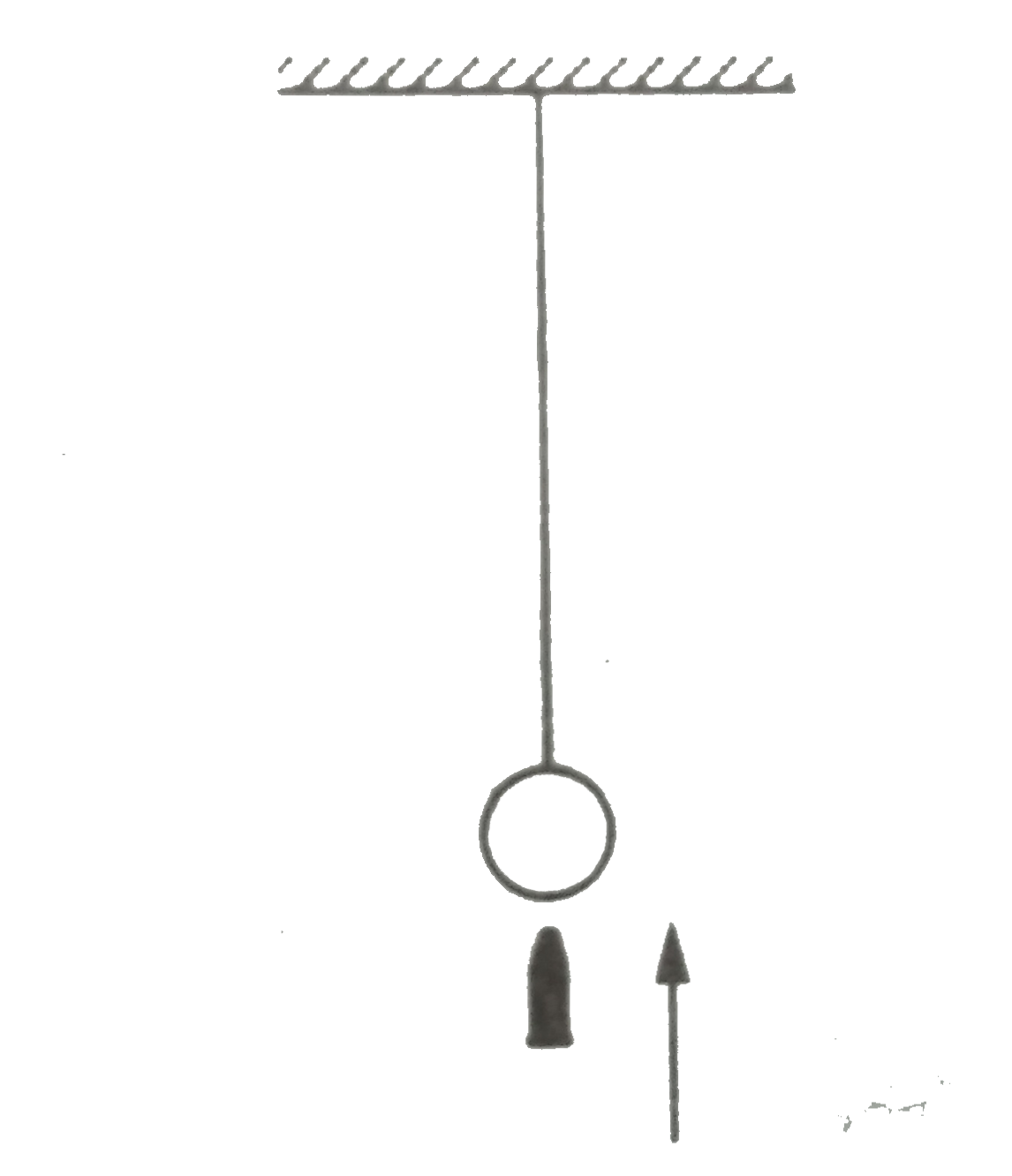
View Solution
A simple pendulum consists of a bob of mass m and a light string of length l as shown in the fig. another identical ball moving with the small velocity v0 collides with the pendulum's bob and sticks to it. For this new pendulum of mass 2 m, mark out the correct statements (s).
View Solution
