Question

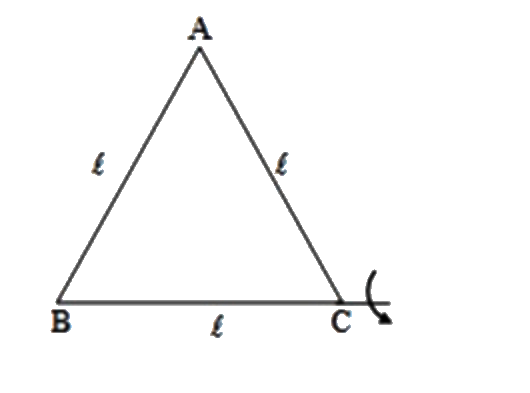
Three identical thin rods, each of mass $m$ and length $l$, are joined to form an equilateral triangular frame. Find the moment of inertia of the frame about an axis parallel to tis one side and passing through the opposite vertex. Also find its radius of gyration about the given axis.

Explanation

To find the moment of inertia of the equilateral triangular frame formed by three identical thin rods about an axis parallel to one side and passing through the opposite vertex, we can follow these steps:

Step 1: Understand the Geometry
We have an equilateral triangle formed by three rods, each of mass \( m \) and length \( l \). We need to find the moment of inertia about an axis parallel to one side (let's say side BC) and passing through the opposite vertex (point A).

Step 2: Identify the Moment of Inertia of Each Rod
1. For Rod AB: The moment of inertia about the axis through A (which is parallel to BC) can be calculated using the parallel axis theorem. The distance from the axis to the center of mass of rod AB is \( \frac{l}{2} \) (since the center of mass of a rod is at its midpoint).
\( I_{AB} = I_{cm} + md^2 = \frac{ml^2}{3} + m\left(\frac{l}{2}\right)^2 = \frac{ml^2}{3} + \frac{ml^2}{4} = \frac{4ml^2 + 3ml^2}{12} = \frac{7ml^2}{12} \)

2. For Rod AC: By symmetry, the moment of inertia of rod AC about the same axis will be the same as that of rod AB.
\( I_{AC} = I_{AB} = \frac{7ml^2}{12} \)

3. For Rod BC: The moment of inertia about the axis through A is simply the moment of inertia about its own center of mass plus the distance squared from the axis to the center of mass. The center of mass of rod BC is at a distance \( d \) from point A, where \( d = l \sin(60^\circ) = \frac{\sqrt{3}}{2} l \).
\( I_{BC} = I_{cm} + md^2 = \frac{ml^2}{3} + m\left(\frac{\sqrt{3}}{2} l\right)^2 = \frac{ml^2}{3} + m\frac{3l^2}{4} = \frac{4ml^2 + 9ml^2}{12} = \frac{13ml^2}{12} \)

Step 3: Total Moment of Inertia
Now, we can sum the moments of inertia of all three rods to find the total moment of inertia \( I \):
\( I = I_{AB} + I_{AC} + I_{BC} = \frac{7ml^2}{12} + \frac{7ml^2}{12} + \frac{13ml^2}{12} = \frac{27ml^2}{12} = \frac{9ml^2}{4} \)

Step 4: Find the Radius of Gyration
The radius of gyration \( k \) is given by the formula:
\( k = \sqrt{\frac{I}{M}} \)
where \( M \) is the total mass of the frame. Since there are three rods, the total mass \( M = 3m \).
\( k = \sqrt{\frac{\frac{9ml^2}{4}}{3m}} = \sqrt{\frac{9l^2}{12}} = \sqrt{\frac{3l^2}{4}} = \frac{l\sqrt{3}}{2} \)

Final Answers
- The moment of inertia of the triangular frame about the given axis is \( \frac{9ml^2}{4} \).
- The radius of gyration about the given axis is \( \frac{l\sqrt{3}}{2} \).