In figure mass m1 slides without friction on the horizontal surface, the frictionless pulley is in the form of a cylinder of mass M and radius R, and a string turns the pulley without slipping. Find the acceleration of each mass, and tension in each part of the string.
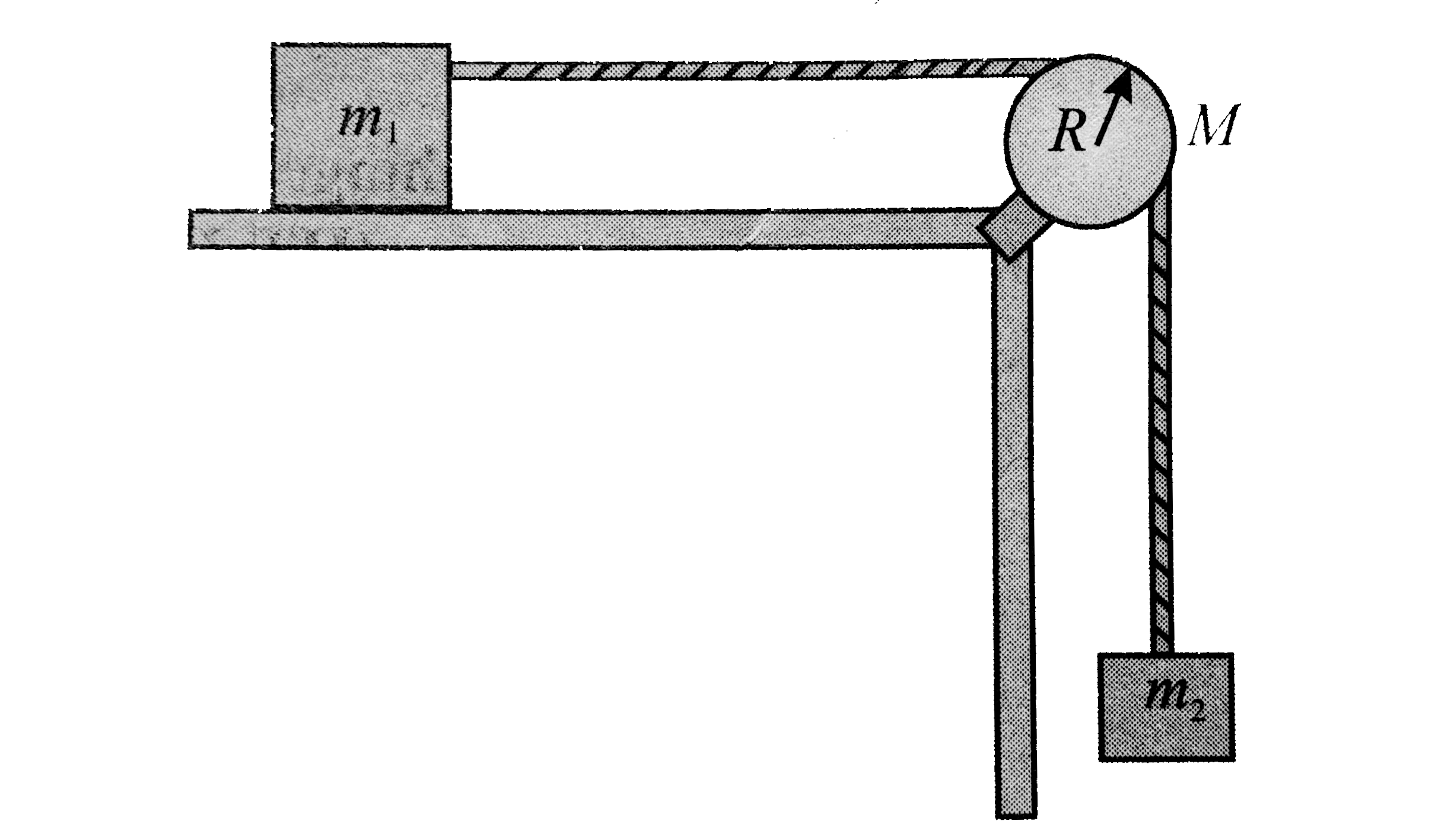
Step I: Analysis of motion: In this case the string rotates the pulley, i.e, the string does niot slide. The puley will have angular acceleration,. Hence, the tension on the string on both the sides of the pulley will not be equal themotion of m1 and m2 will be translational. Positive direction of angular acceleration α is taken along the corresponding acceleration a1 which is taken positive in the direction of not force.
Step II: Equation of motion: Let these be T1 and T2. The equation of motion respectivley, of masses m1 and m2 is
T1=m1a..........i
and m2g−T2=m2a ........ii
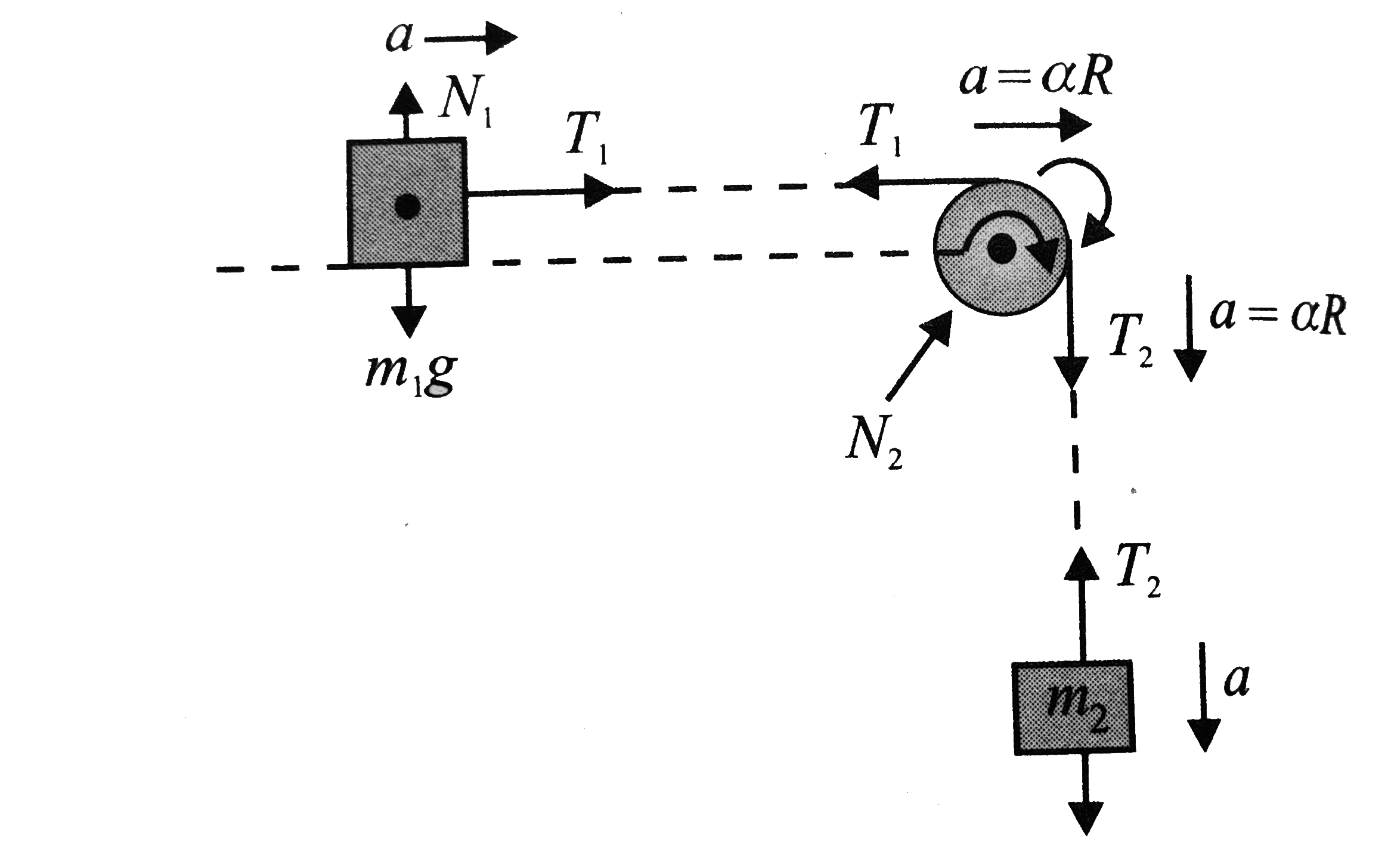
Step III: Application of torque equation
The torque equation for the pulley.
T2R−T1R=Iα.......iii
(N2 constitutes no torque about the axis of rotation)
There is no slipping of the string over the pulley.
a=αR⇒α=aR ............iv
From eqwn iii and iv we get
∴T2R−T1R=IaR
or T2−T1=IaR2...........v
Step V: Solving equations:
Solving the above equation we get a=m2g(m1+m2+IR2)
Here I=MR22
T1=m1m2g(m1+m2+IR2) and T2=(m1+IR2)m2g(m1+m2+LR2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
The strings are inextensible and light: the pulleys are smooth and light. Find the acceleration of each block and tensions in the strings.
 View Solution
View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.
 View Solution
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
View SolutionIf the string & all the pulleys are ideal, acceleration of mass m is :-
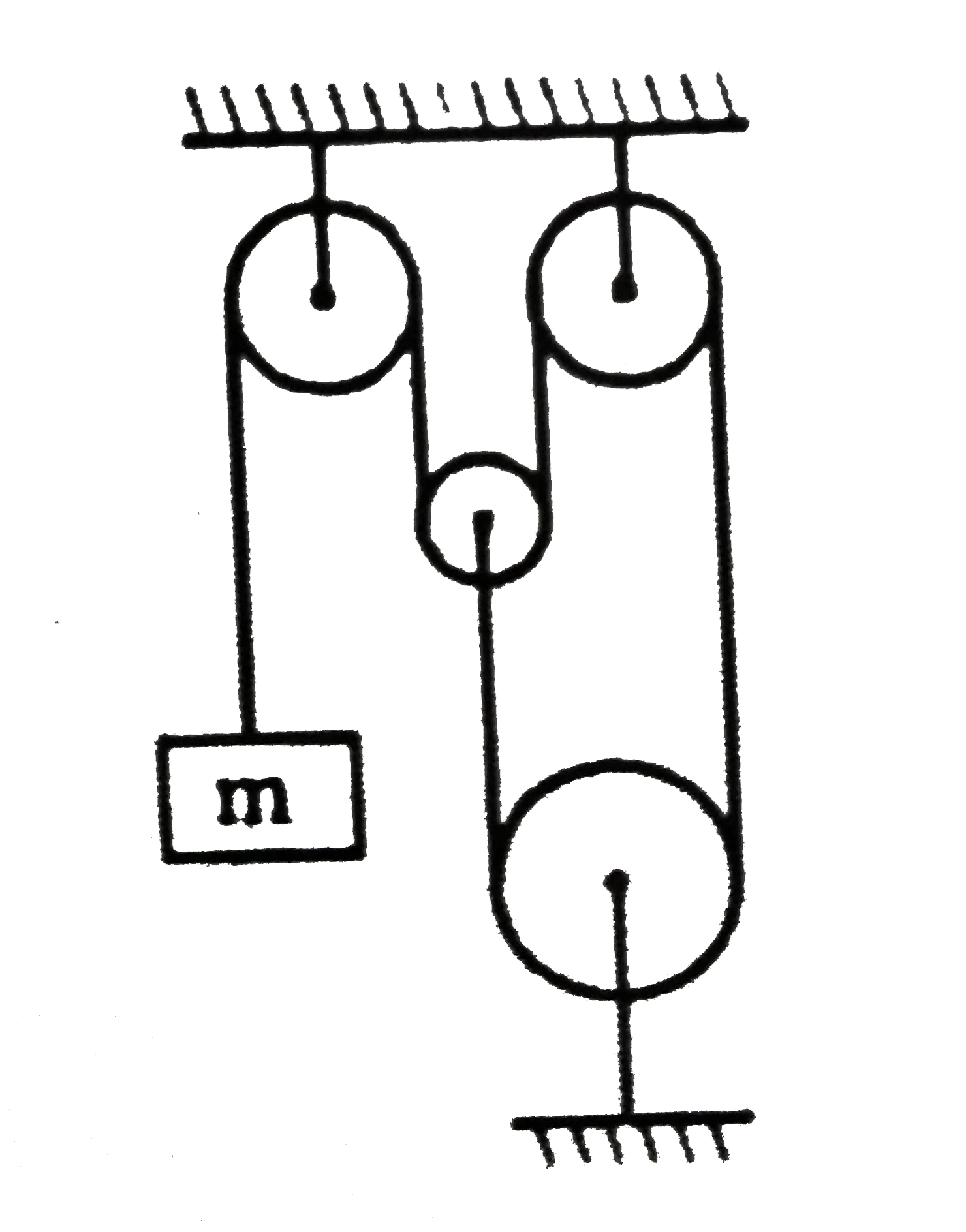 View Solution
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View SolutionA mass M is hung with a light inextensible string as shown in Find the tension in the horizontal part of the string .
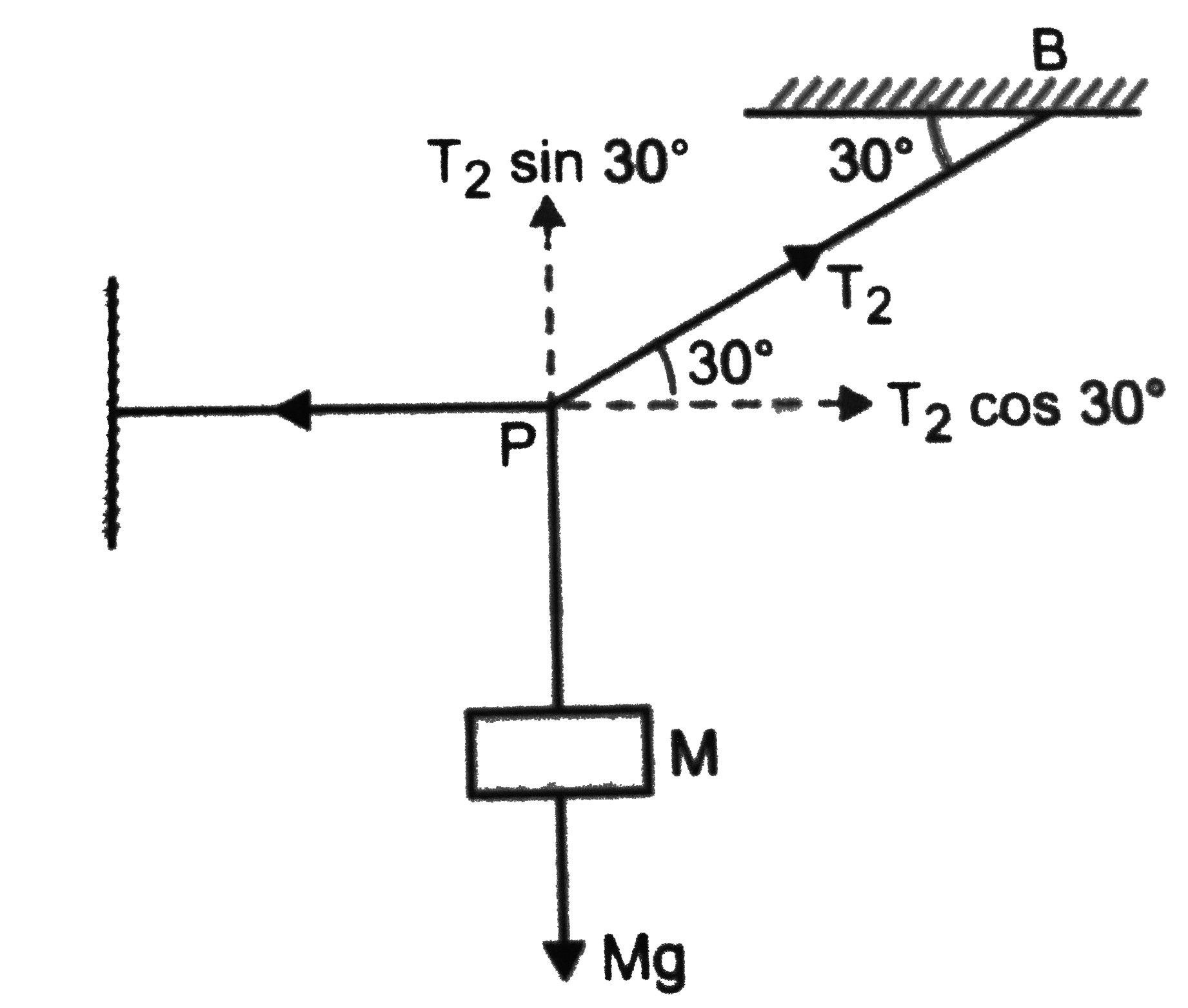 View Solution
View SolutionA load of mass m is attached to the end of a string wound on a cylinder of mass M and radius R. The string passes round a pulley.
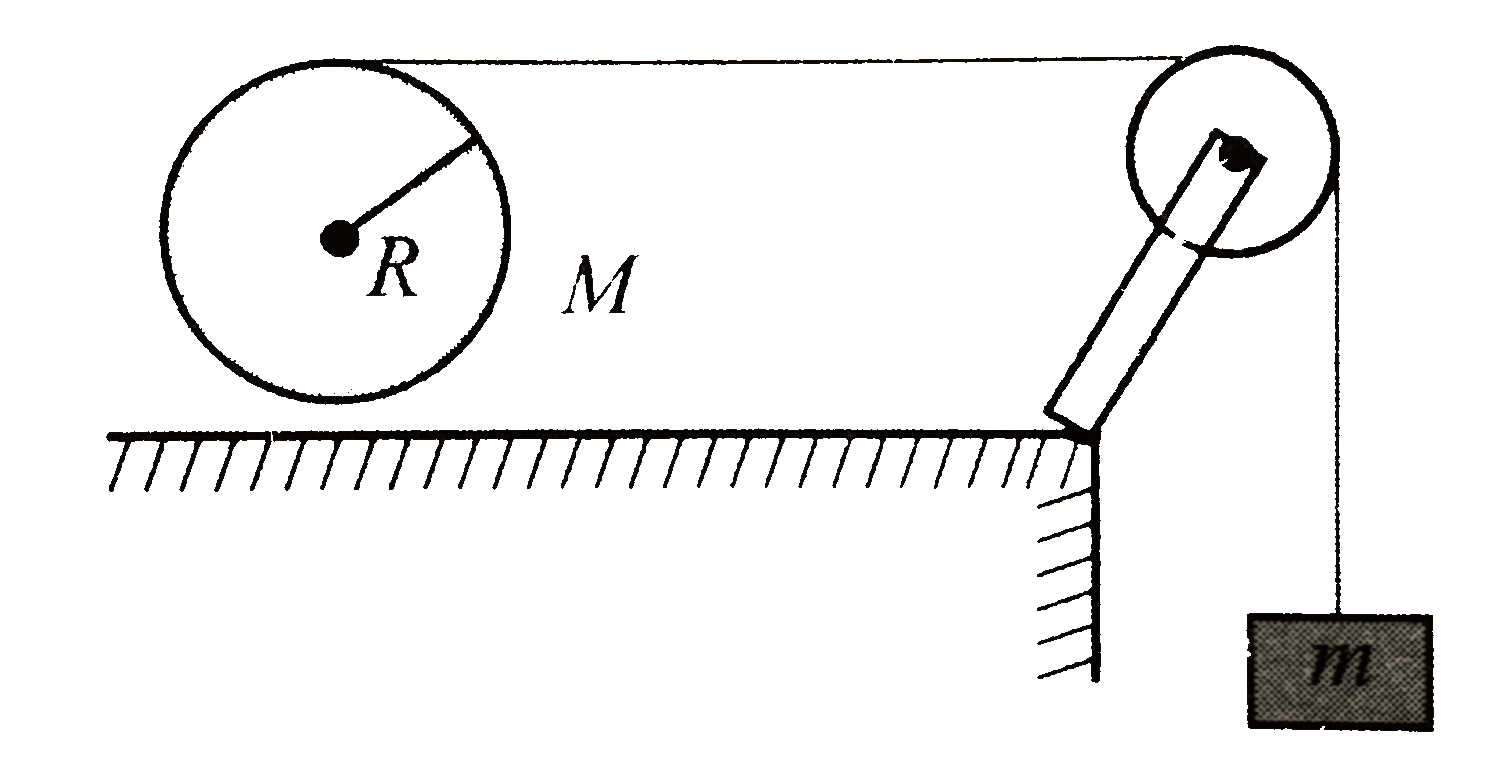
a. Find the acceleration of the cylinder M when it rolls.
b. If the coefficient of friction is μ. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls alwaysView SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View SolutionA mas m hangs with help of a string wraped around a pulley on a frictionless bearling. The pulley has mass m and radius R. Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass m, if the string does not slip on the pulley, is:
View SolutionWhat is the mechanical advantage of single fixed pulley:-
 View Solution
View Solution

