A block of mass m height 2h and width 2b rests on a flat car which moves horizontally with constant acceleration a as shown in figure. Determine

a. the value of the acceleration at which slipping of the block on the car starts, if the coefficient of friction is μ.
b. the value of the acceleration at which block topples about A, assuming sufficient friction to prevet slipping and
c. the shortest distance in which it can be stopped from a speed of 20ms−1 with constant deceleration so that the block is not disturbed. The following data are given b=0.6m,h=0.9m,μ=0.5 and g=10ms−2
a. Maximum frictionnal force between block and car will be limiting force.

⇒fmax=μmg
The maximum possible acceleration of block can be
amax=fmaxm=μmgm=μg=(0.5)(10)=5ms−2
if acceleration of car, exceeds this value slipping will start between the block and the car.
b. In the case when the block is about to topple about P, normal reaction will pass through P. The friction will be static nature.
f=ma ............i
N=mg.......ii
the block topples when torque of f about CM exceeds the torque of N.
The block topples when torqe of f about CM exceeds the torque of N.
In case of the limiting valueτf=τN
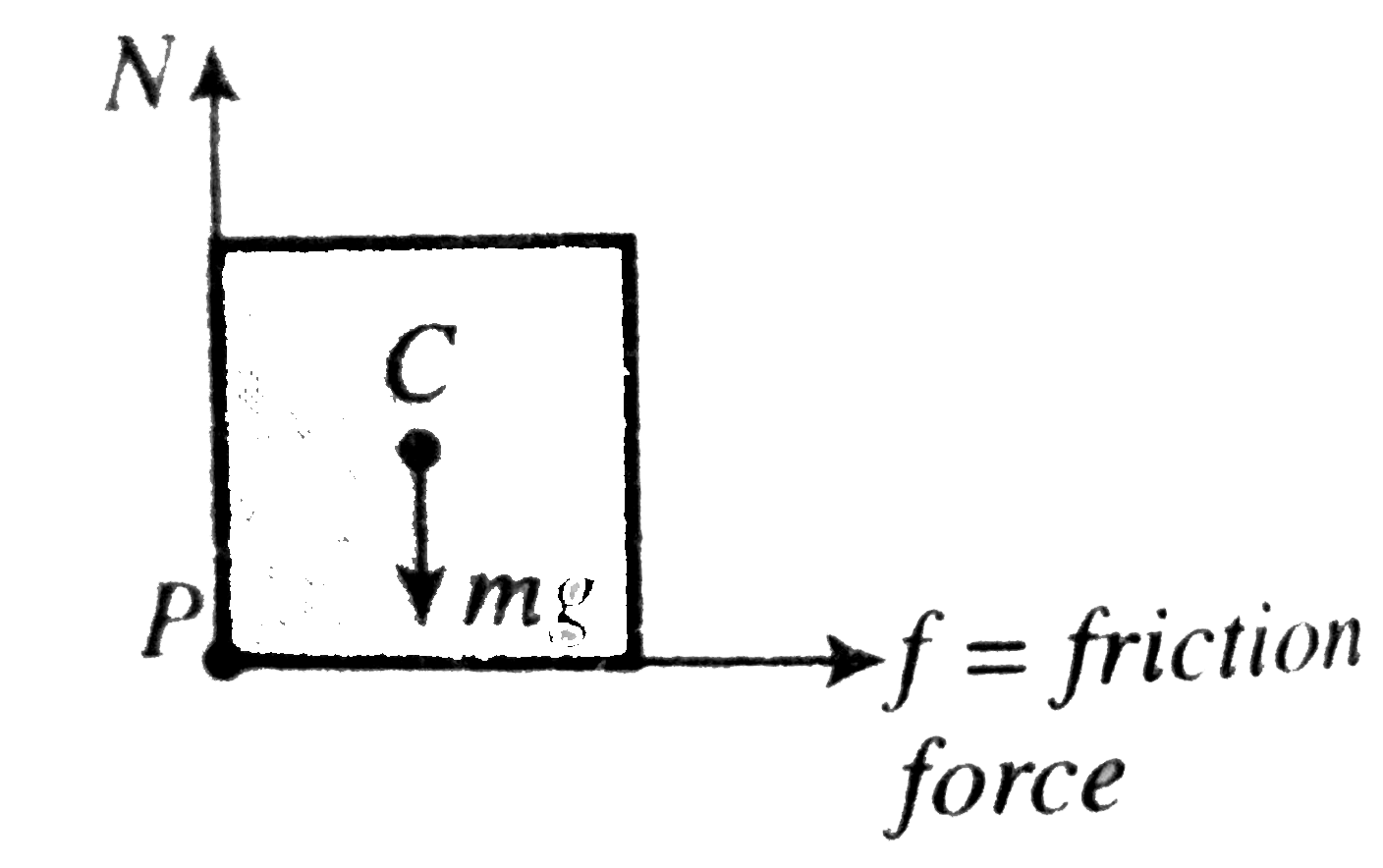
or (f)(h)=(N)(b)
(ma)(h)=(mg)(b)
or a=(bh)g=(0.60.9)(10)=609ms−2
so, if the acceleration of car exceeds this value the block will topple about A.
c. the maximum acceleration /retardation at which the block is not disturbed, is the smaller of the two values, obtained above i.e, 5ms−2
Hence the maximum retardation can be 5ms−2
Now using v2=u2−2as
Initial velocity u=0
s=u22a(a=5ms−2)=(20)2(2)(5) or s=40m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.217videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View SolutionA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it isView SolutionAcceleration of block A varies with time as shown in figure the value of coefficient of kinetic friction between block A and B is
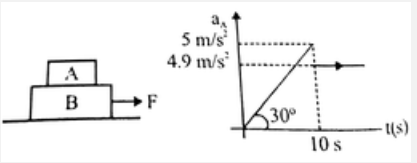 View Solution
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
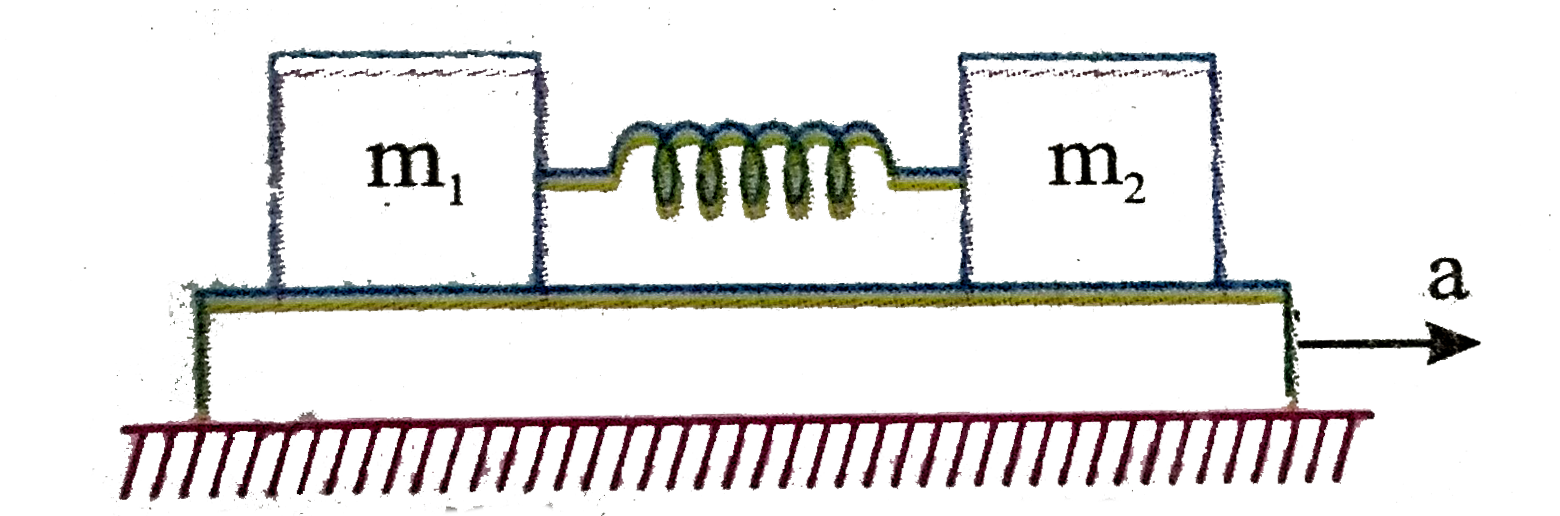 View Solution
View SolutionA block of mass 4kg is pressed againest the wall by a force of 80N as shown in figure Determine the value of the friction force and block's acceleration (Take μs=0.2,μs=0.15)
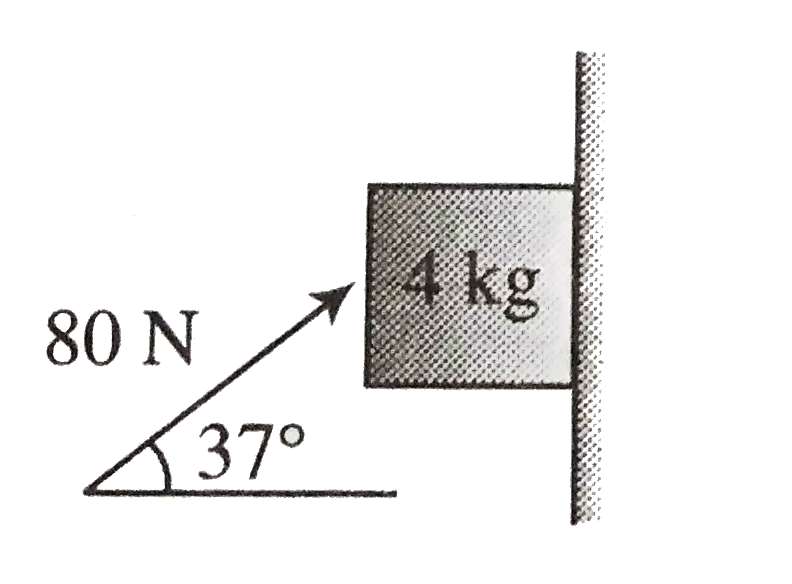 View Solution
View SolutionFriction coefficient between block and inclined plane is [μ=1√3] if lift is moving vertically down with constant acceleration a then the value of acceleration a so that block moves down with constant velocity is
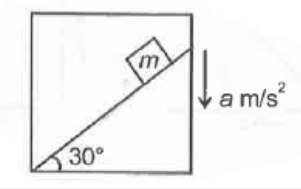 View Solution
View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block isView SolutionFor the arrangement shown in the figure the coefficient of friction between the two blocks is μ. If both the blocks are identical and moving ,then the acceleration of each block is
 View Solution
View SolutionA block rests on a horizontal table which is executing SHM in the horizontal plane with an amplitude A. What will be the frequency of oscillation, the block will just start to slip? Coefficient of friction=μ.
View SolutionA wooden block of mass m resting on a rough horizontal table is pulled by a force F as shown in the figure. If μ is the coefficient of friction between block and table, its acceleration will be
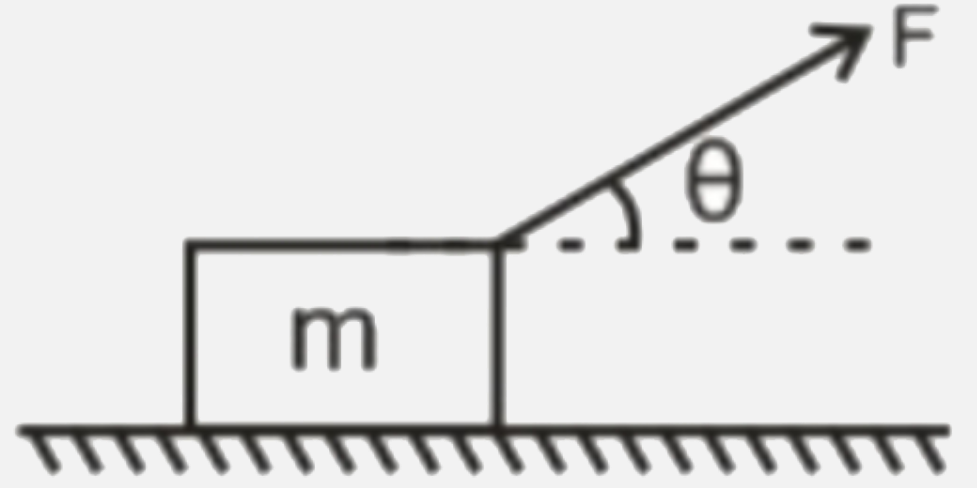 View Solution
View Solution

