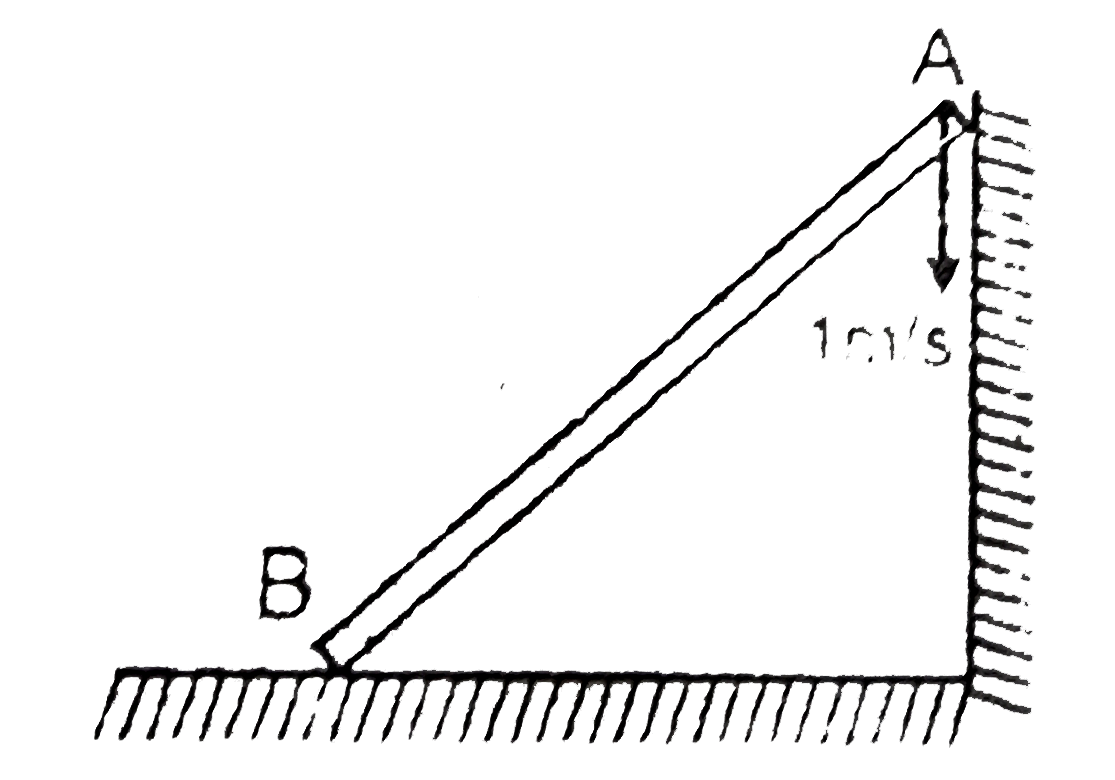
A rod length which remains in vertical plane has its ends and constrained to remain contact with a horizontal floor and a vertical wall respectively. Determine the velocity of the end and angular velocity at the position shown in Fig. , if the point has a velocity of rightward.

Velocity of end is horizontal while velcity of the end is vertical downward. For finding the positin of instntanneous centre of rotation. Drop perpendicular to the directins of and at points and respectvely. The intersection point be the instantaneous centre.
For the end
For the end

Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.2
Explore 17 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.3
Explore 15 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Solved Examples
Explore 9 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
A point on the rim of a wheel 3 m in diameter has linear velocity of 18 ms−1 . The angular velocity of the wheel is
View SolutionA rod of length l is moving in a vertical plane (x−y) when the lowest point A of the rod is moved with a velocity v. find the a angular velocity of the rod and b velocity of the end B.

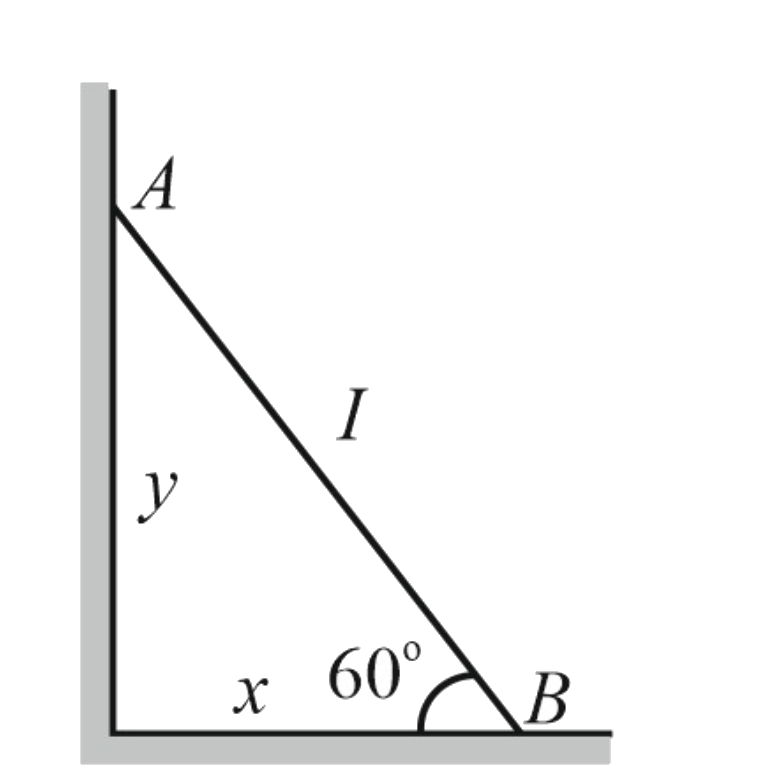
View SolutionA rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
View SolutionA light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.

View SolutionA thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
View SolutionA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
View SolutionThe velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is

View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View SolutionA rod length AB is moving with ends remaining in contact with frictionless wall and floor . If at the instant shown , the velocity of the and B is 3ms−1 towards the negative x-direction , then the magnitude of the velocity of the end A wll be
View Solution
