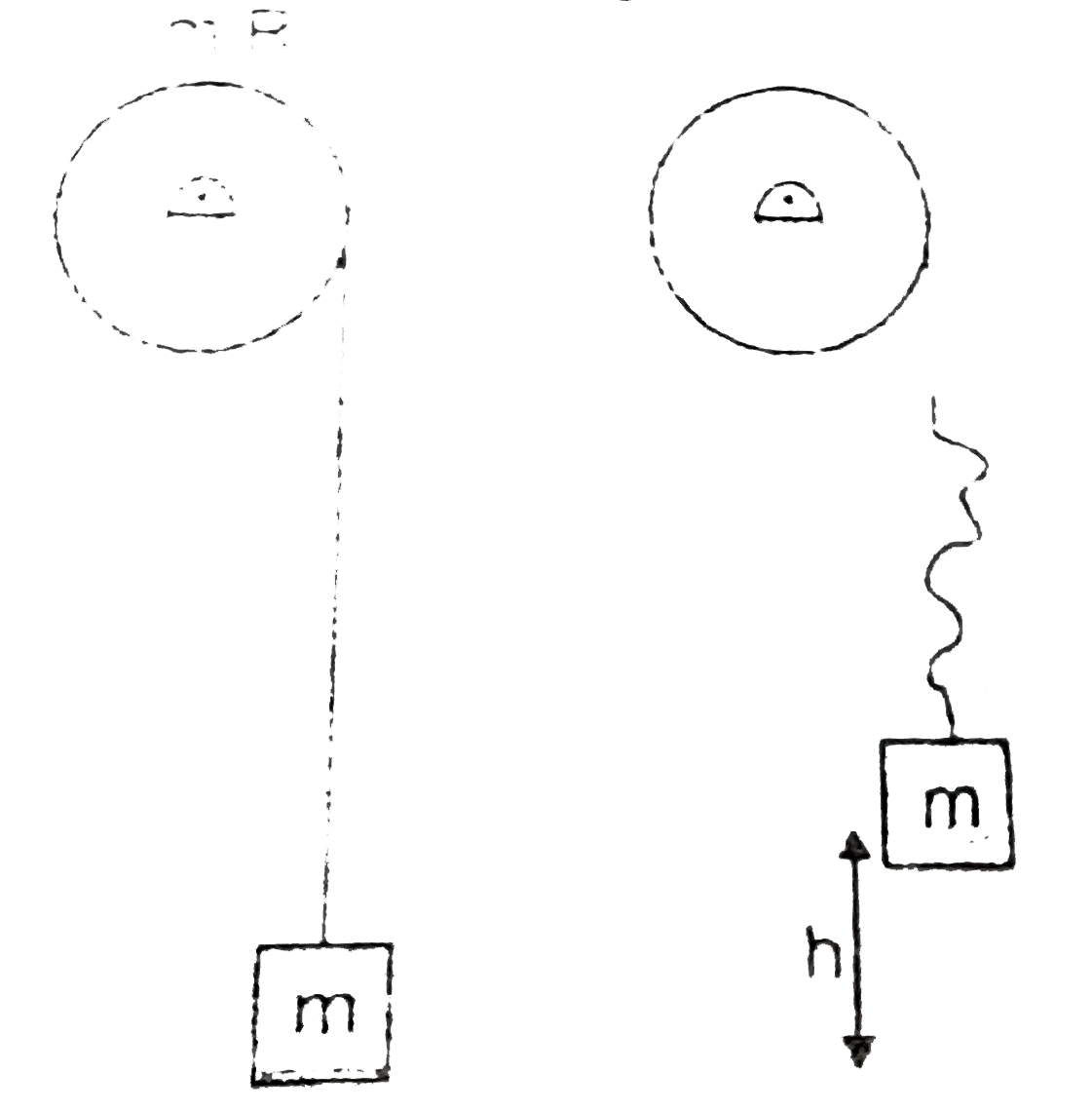
A string is wrapped several times on a cylinder of mass M and radius R. the cylinder is pivoted about its adxis of block symmetry. A block of mass m tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance h, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity ω0 of the cylinder ,the speed v0 of the falling body, m and the kinetic energy K0 of the system.
b. Evaluate the corresponding quanitities ω1,v1 and K1 for the instant just after the string becomes taut.
c. Why is K1 less than K0? Where does the energy go?
d. If M=m, what fraction of the kinetic energy is lost when the string becomes taut?
a. Just before the stirng becomes taut, the block falls freely, so v0=√2gh, There is no tension in the string so nothing causes the cylider to spin so ω0=0. The kinetic energy of the system is K0=12mv20+12lω20=mgh.
b. When the string experiences a jerk, the large impulse developed of very short duration so that the contribution of weight mg can be neglected during this time interval. The angular momentum of the system is conserved, as the tension is internal force for the system. Thus we have
→Li=→Lf
mv1R+12MR2ω1=mv0R=m√2ghR
The string is inextensible so v1=Rω1. On solving for ω1, we get ltbr ω1=√(2gh)R[1+(M2m)],v1=Rω1=⎛⎜
⎜⎝√2gh[1+(M2m)]
The final kinetic energy K1 is given by
K1=12mv21+ω21
=12mv21+12(12MR2)(v21R2)=12(m+M2)v21
=12⎡⎢
⎢⎣mv201+(M2m)⎤⎥
⎥⎦=K01+(M2m)
c. The situation in this case is analogous to the energy loss is complete inelastic two body collisions. The lost kinetic energy is converted to heat energy or elastic potential energy of the string or in the two objects.
d.For M=m,K1=2K03, so the fraction lost is
(K0−K1K0)=13
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples12videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View SolutionThe block of mass m is at rest. Find the tension in the string A .
 View Solution
View SolutionA solid cylindrical pulley of mass m and radius R=10cm is hinged about its horizontal axis of symmetry. A light spring is wrapped around it, and small block of mass 'm' is suspended from the string. Now the block is lefted vertically by a distance h = 1.8 m and released. Just after the string becomes taut again, find the angular velocity of the cylinder in rad/s (Take g=10m/sec2)
 View Solution
View SolutionA blocked of mass m is attached with two strings as shown in figure .Draw the free body diagram of the block.
 View Solution
View SolutionA block of mass m is attached with two strings as shown in figure .Draw the free body diagram of the block.
 View Solution
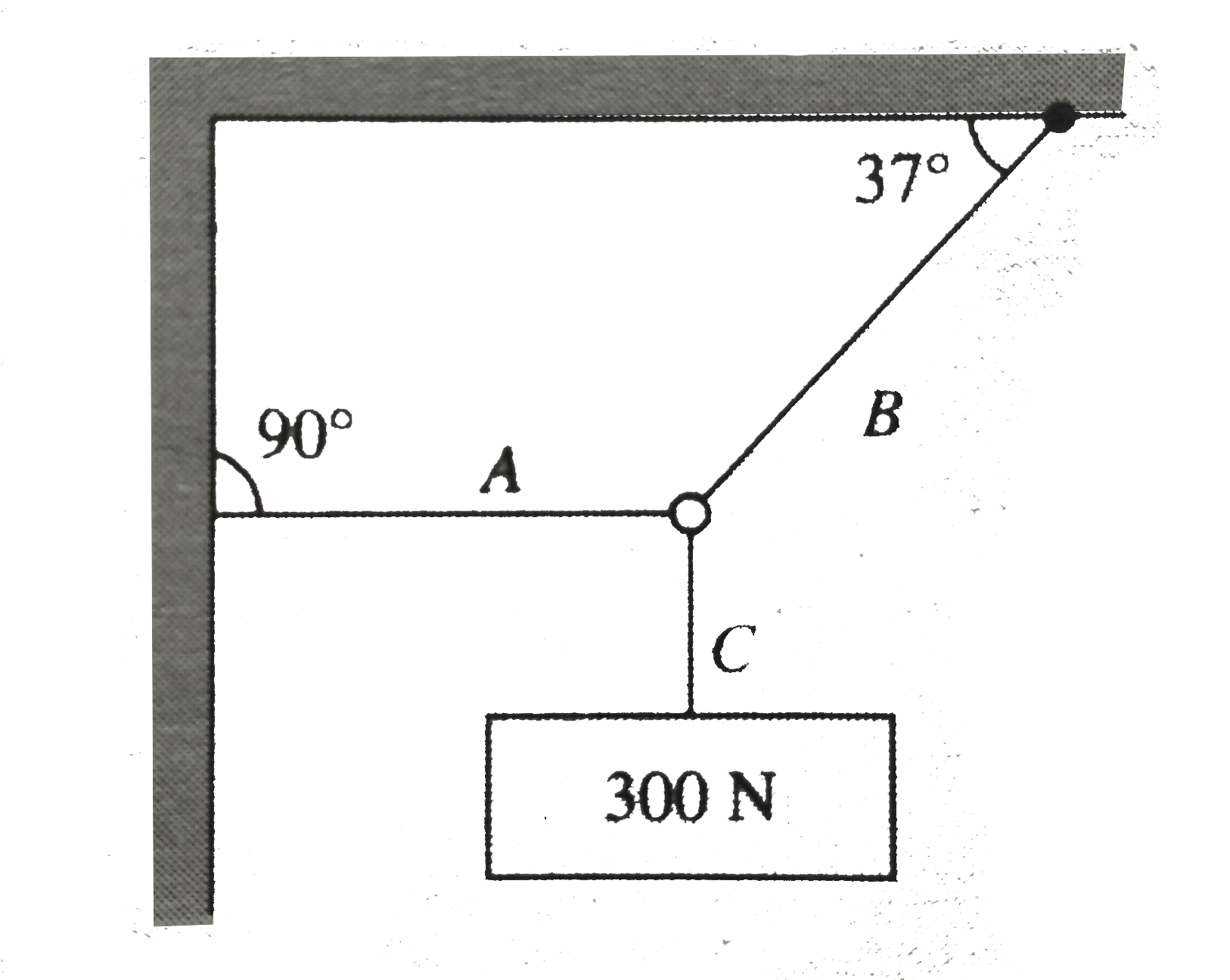
View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.
 View Solution
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View SolutionA string is warapped around a cylinder of mass m and radius r. The string is also connected to a block of same mass m with the help of another pulley as shown in figure. The angular acceleration of the cylinder is ( friction is sufficient for rolling ) ( all pulleys are ideal)
 View Solution
View Solution

