A particle of mass m is released from rest at point A in Fig., falling parallel to the (vertical) y-axis. Find the angular momentum of the particle at any time t with respect to the same origin O.
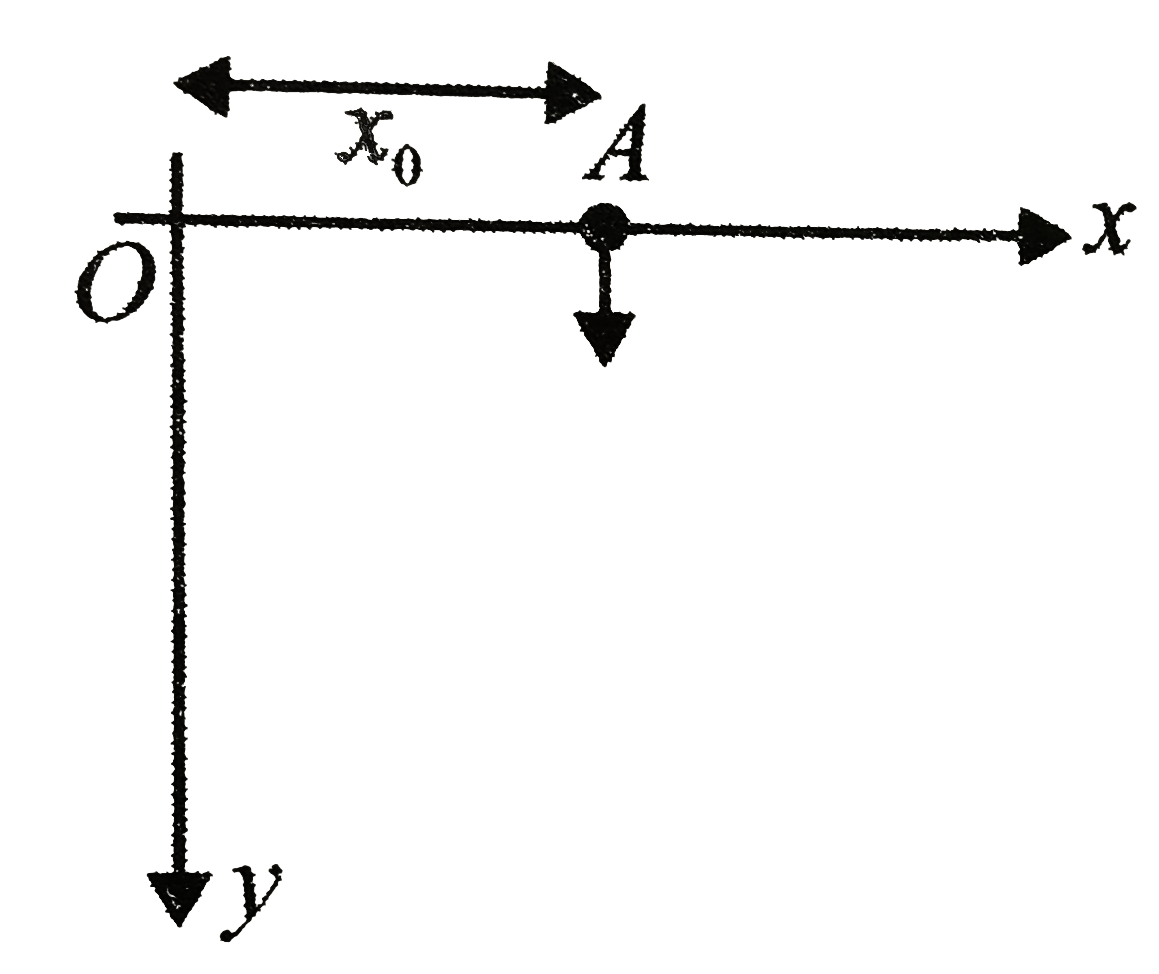
→L=→r×→p
The magnitude of →L is given by L=rpsinθ(ˆk)
in this example velocity of the particle at any time
v=gt,rsinθ=x0 and p=mv=mgt
∴→L=mgx0t(ˆk)……..i
The right hand rule shows that →L is parallel to torque, i.e. direcrected perpedicular to paper in wards.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.3
21 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A charged particle of mass m and charge q is released from rest the position (x0,0) in a uniform electric field E0ˆj. The angular momentum of the particle about origin.
View SolutionA particle of mass m is released in vertical plane from a point P at x=x0 on the x-axis. It falls vertically parallel to the y-axis. Find the torque τ acting on the particle at a time about origin.

View Solution
Knowledge Check
Consider a particle of mass m having linear momentum →p at position →r relative to the origin O. Let →L be the angular momentum of the particle with respect to the origin. Which of the following equations correctly relate(s) →r, →p and →L?
Ad→Ldt+→r×d→pdt=0Bd→Ldt+d→rdt×→p=0Cd→Ldt−d→rdt×→p=0Dd→Ldt−→r×d→pdt=0
A particle of mass m is projected with a velocity v at an angle of θ with horizontal. The angular momentum of the particle at the highest point of its trajectory is equal to :
View SolutionA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is

View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View SolutionA particle of mass m is projected with a speed v at an angle θ with the horizontal. Find the angular momentum of the particle about an axis passing through point of projection and perpendicular to the plane of motion of the particle.
(a) When the particle is at maximum height and
(b) When the particle is just about to collide with the horizontal surface
View SolutionA particle of mass m is projected from origin O with speed u at an angle θ with positive x-axis. Positive y-axis is in vertically upward. Direction. Find the angular momentum of particle at any time t about O before the particle strikes the ground again.
View SolutionA particle of mass m is projected with a speed u at an angle θ to the horizontal at time t=0. Find its angular momentum about the point of projection O at time t, vectorially. Assume the horizontal and vertical lines through O as X and Y axes, respectively.
View SolutionA particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
View Solution
