Two identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs , vr as a function of time is best represented by
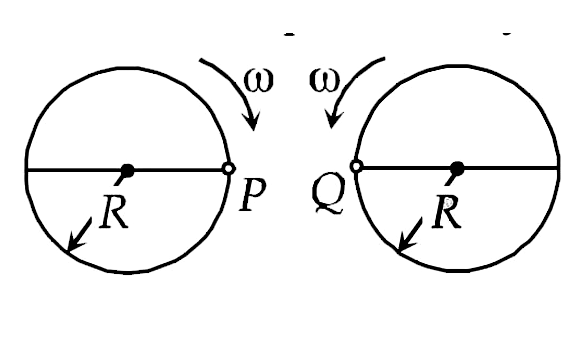
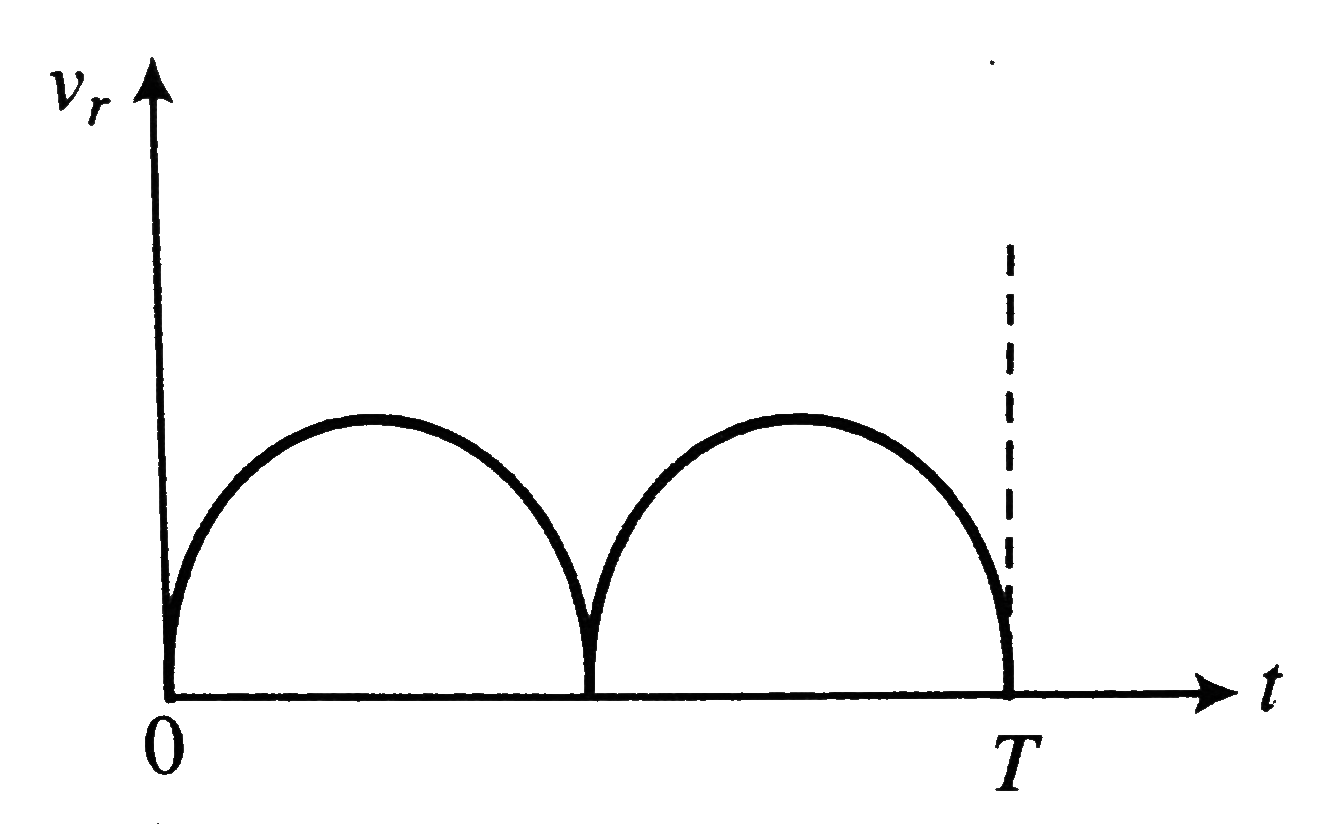
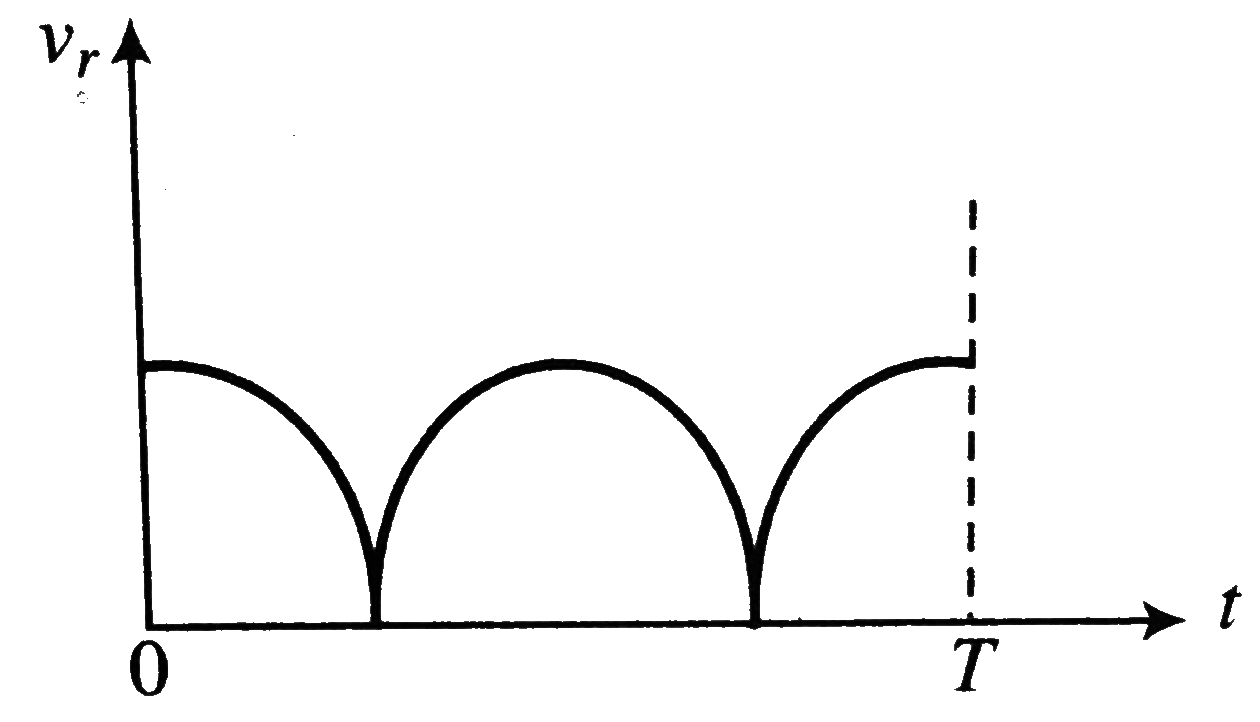
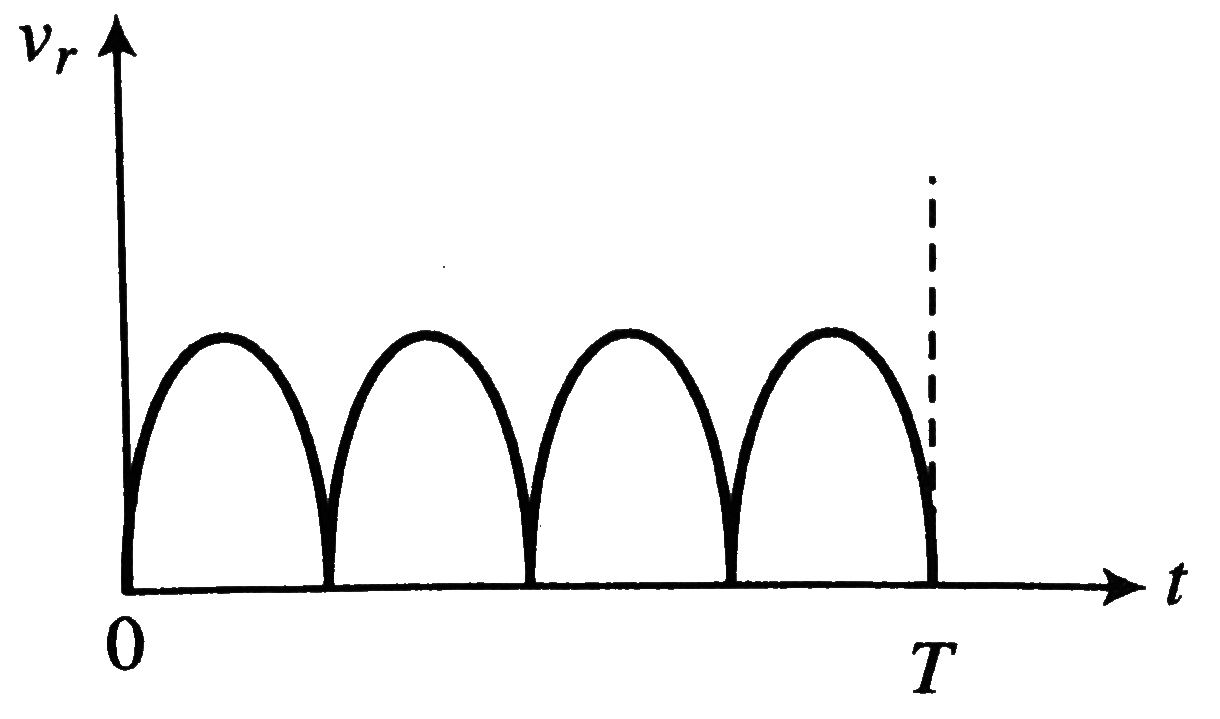
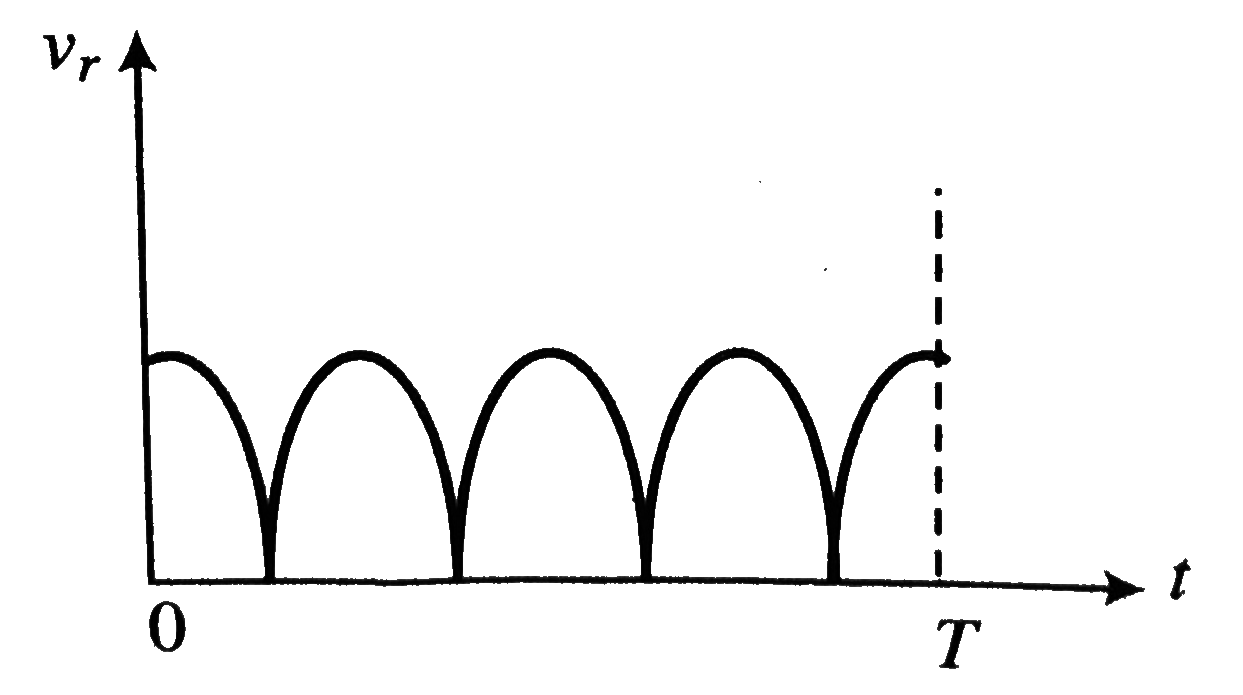
The correct Answer is:A

Vr=|2vsinθ|=|2vsinωt|
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - MCQ_TYPE
14 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - AR_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - True/False
4 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A disc of radius R start at time t=0 moving along the positive X-axis with linear speed v and angular speed ω. Find the x and y-coordinates of the bottommost point at any time t.
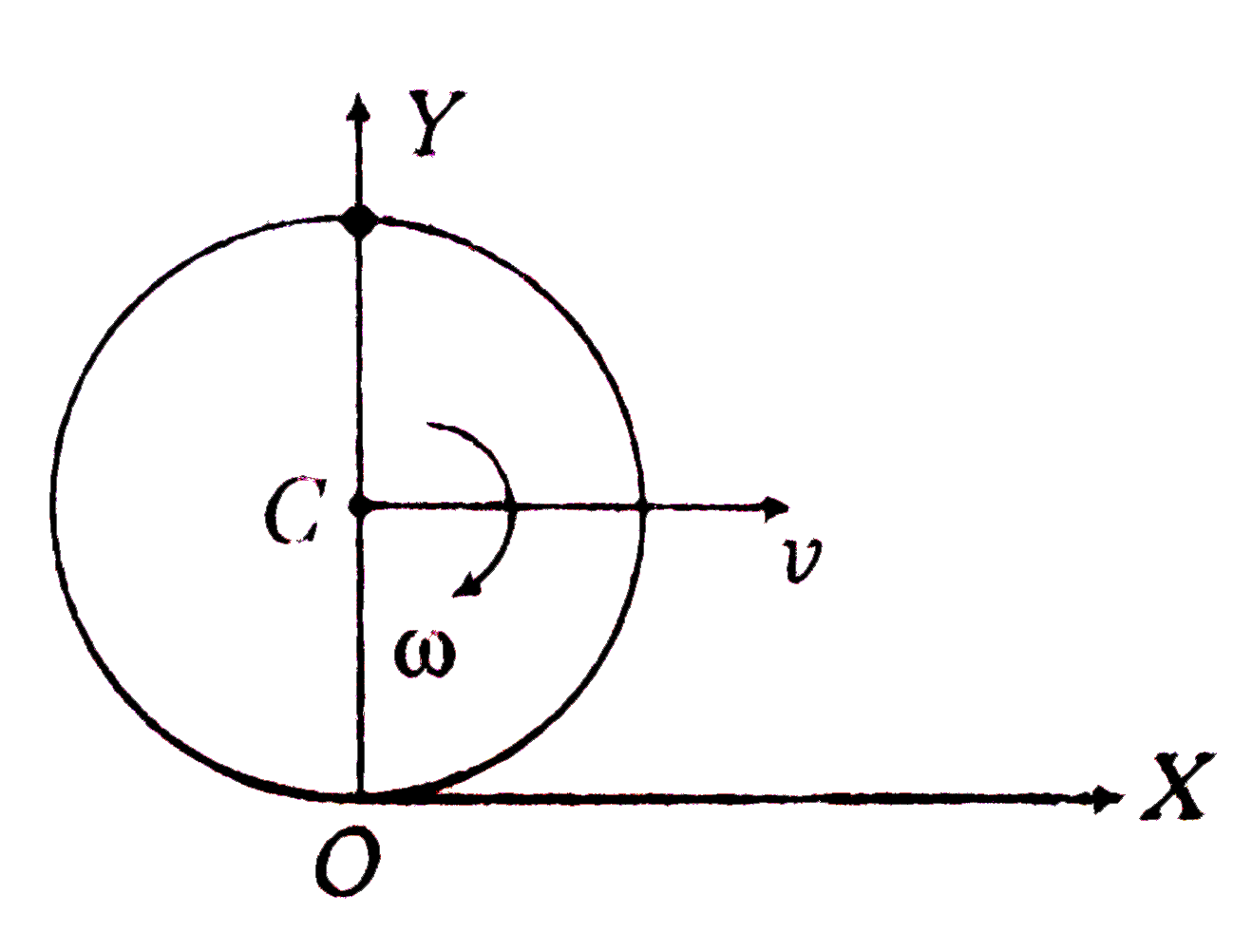
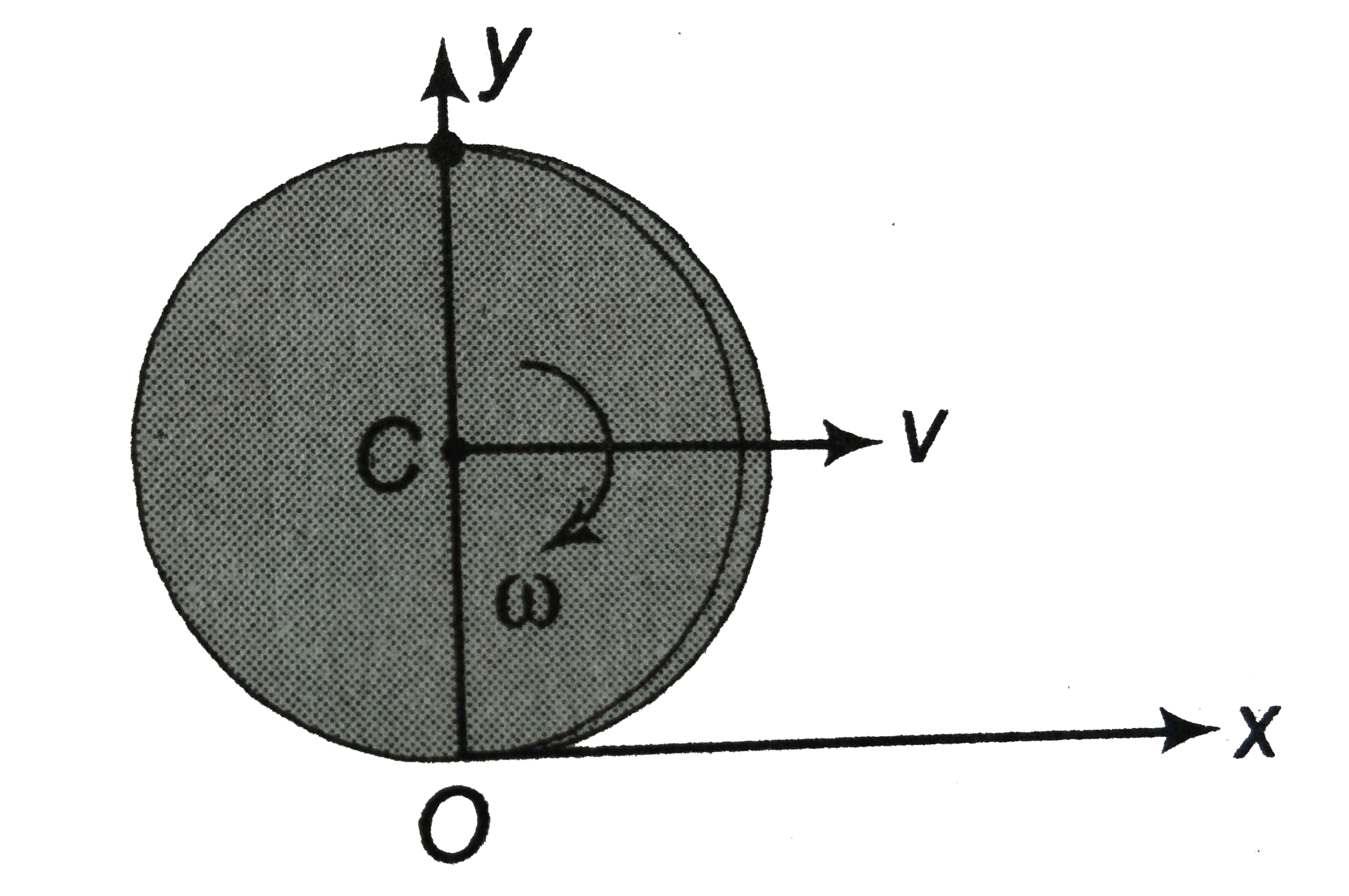
View SolutionA disc of radius R starts at time t=0 moving along the positive x-axis with linear speed v and angular speed ω. Find the x and y coordinates of the bottom most poitn at any time t.
View SolutionTwo trains going in opposite directions with the same speed are at rest relative to each other. True/False.
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View SolutionTwo particles P and Q are moving as shown in the figure. At this moment of time the angular speed of P w.r.t. Q is
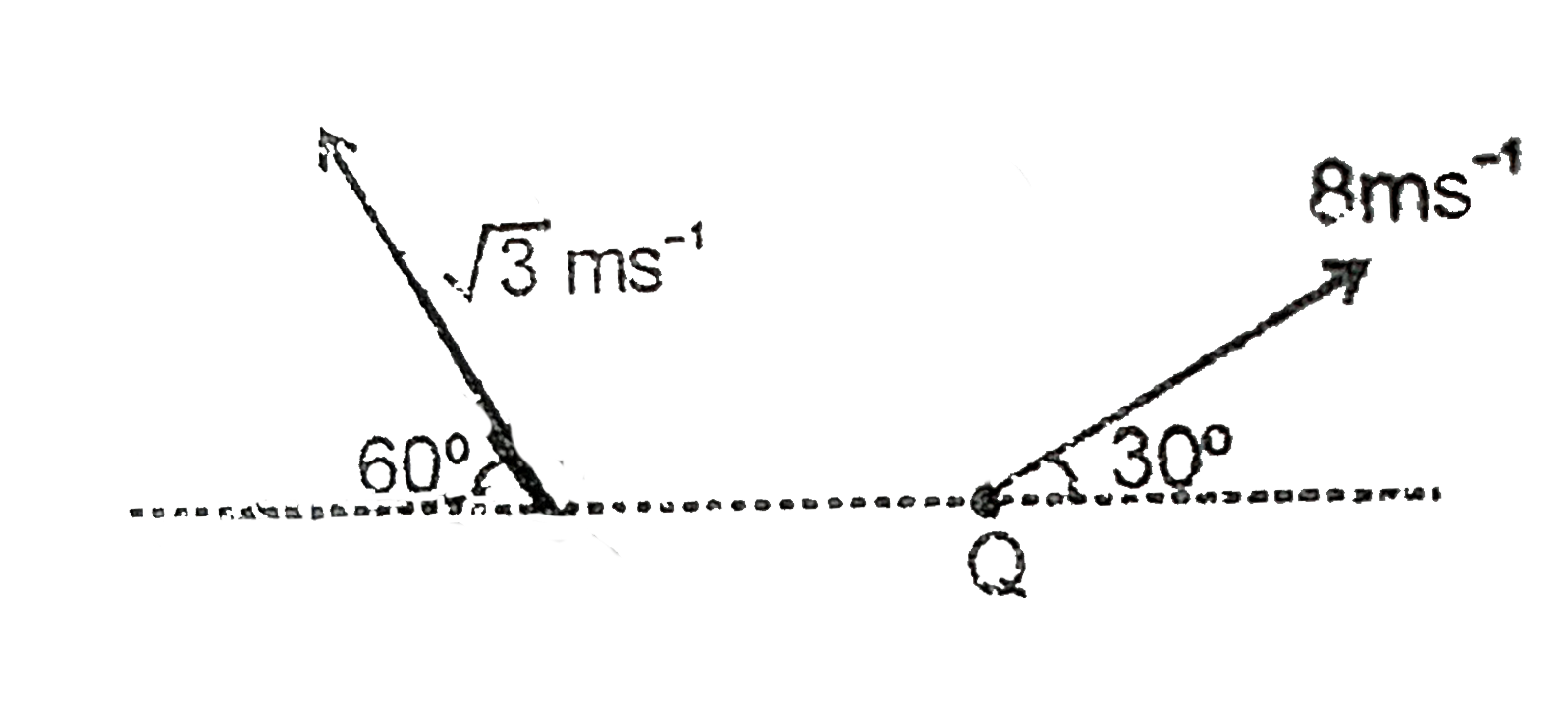
View SolutionTwo cars are moving is one a same line dimension in opposite direction with the same speed v. The relative velocity of two cars w.r.t. each other is
View SolutionTwo point P and Q. diametrically opposite on a disc of radius R have linear velocities v and 2v as shown in figure. Find the angular speed of the disc.
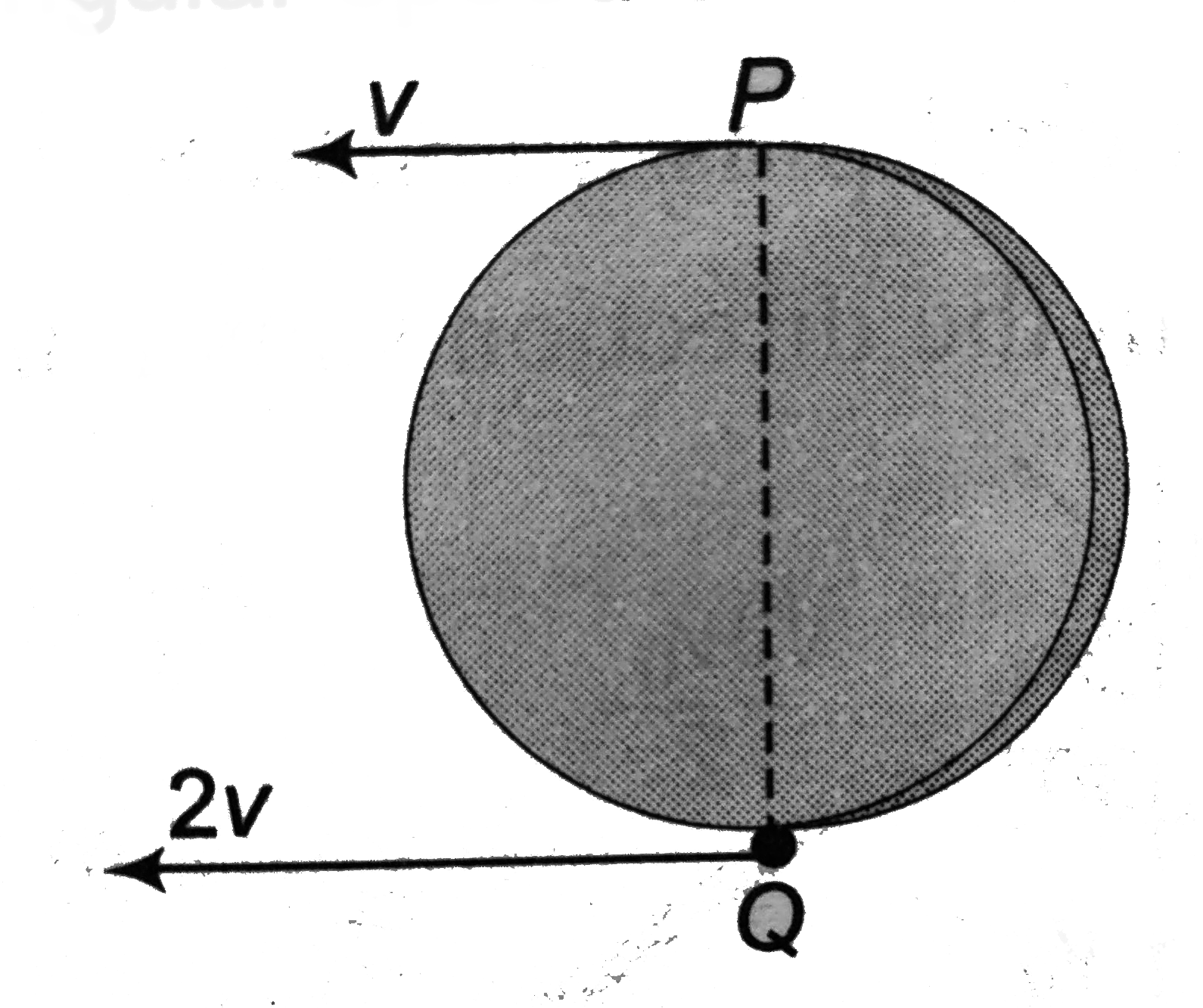
View SolutionA disc is freely rotating with an angular speed ω on a smooth horizontal plane. If it is hooked at a rigid pace P and rotates without bouncing about a point on its circumference. Its angular speed after the impact will be equal to.
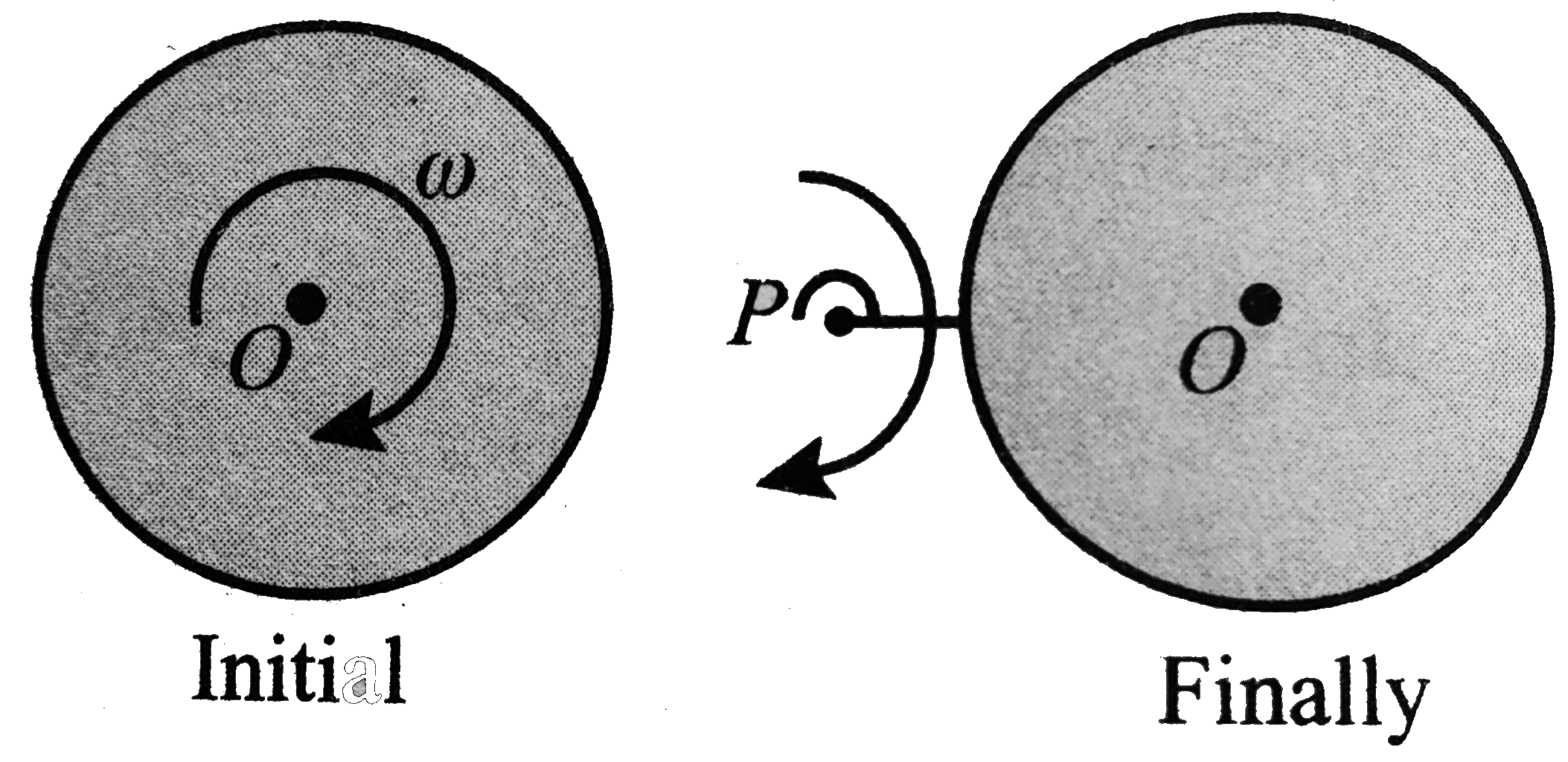
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.
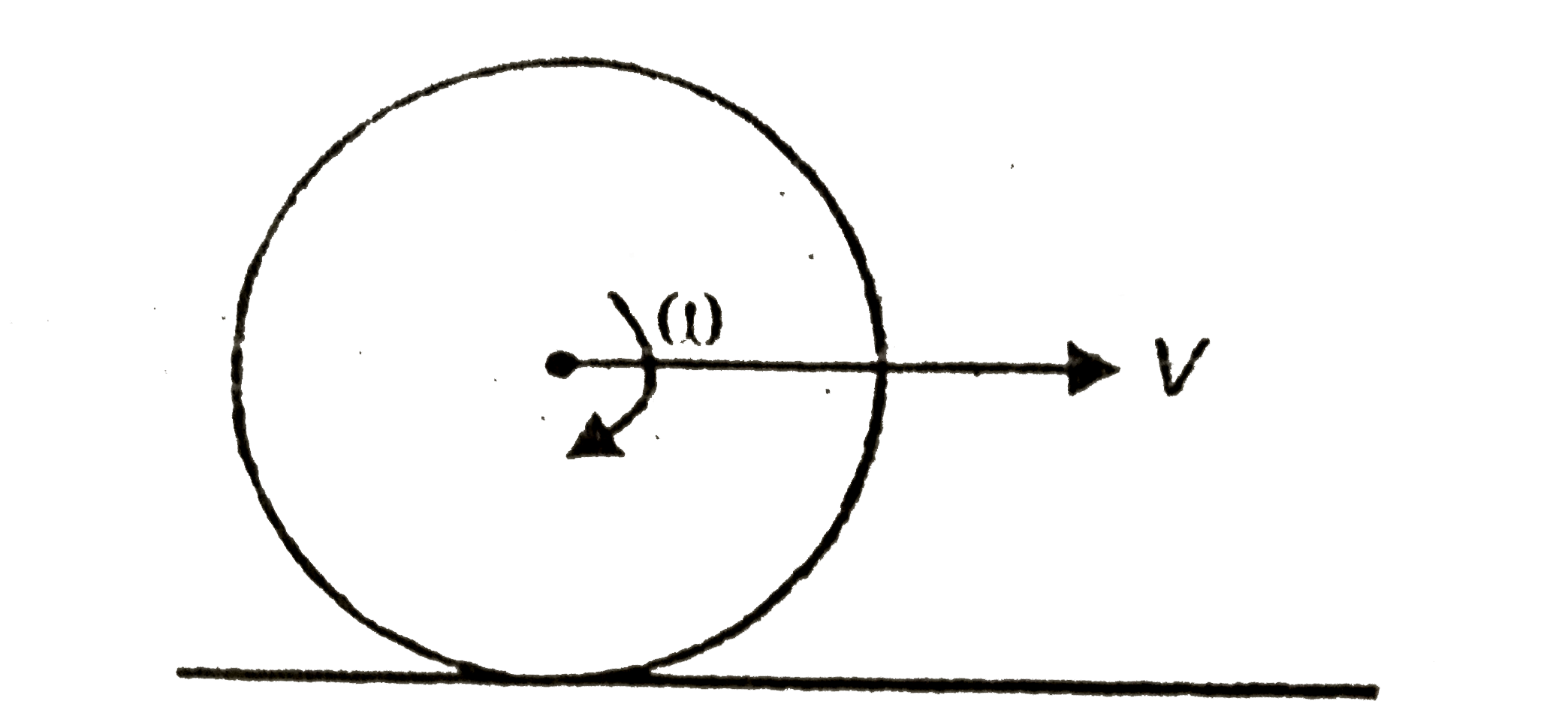
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
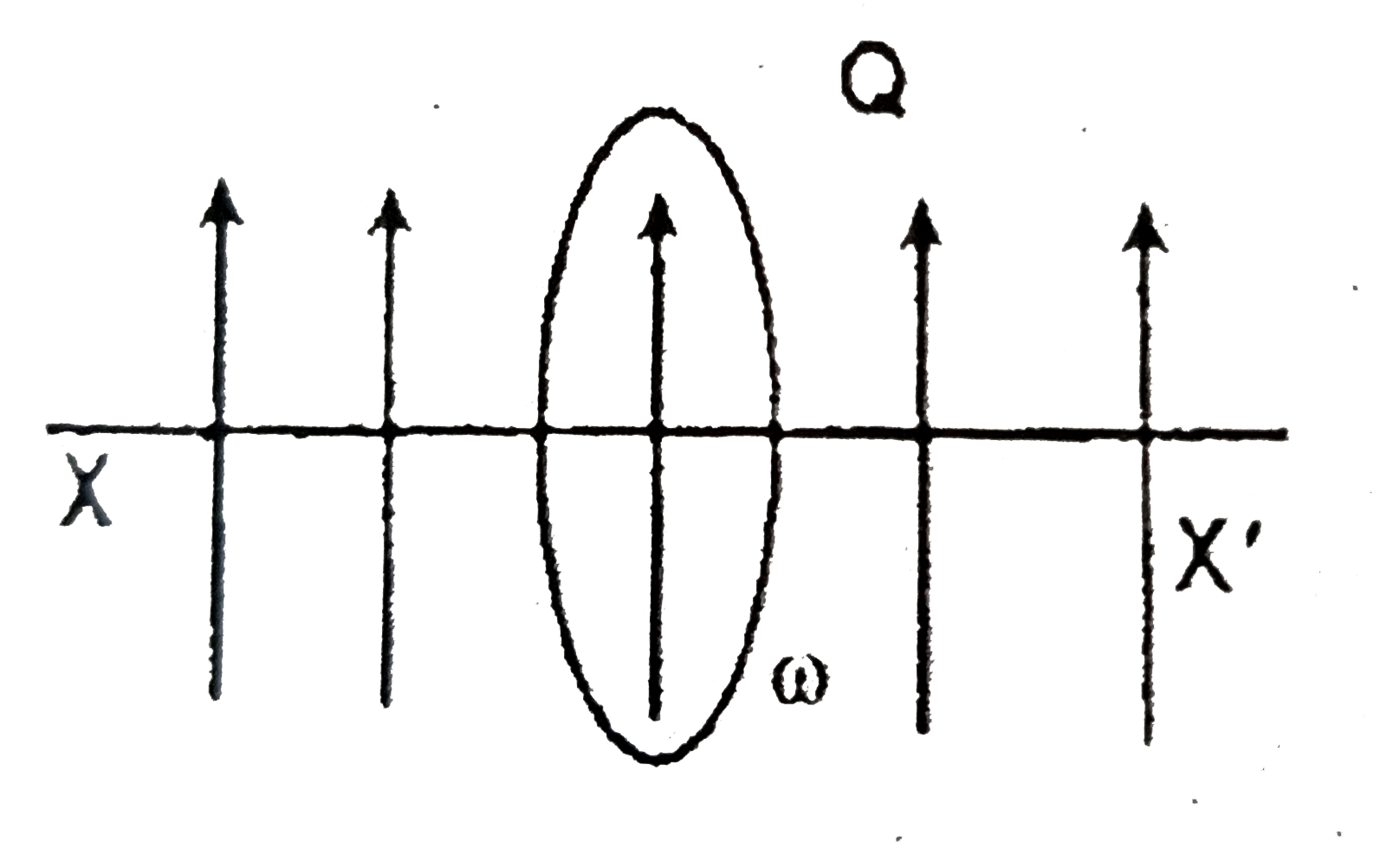
View Solution
