A tank of square cross section (2m×2m) is filled with water up to a height of 2.5m. Find the thrust experienced by the vertical and botom of the tank (g=10m/s2).
To solve the problem, we need to calculate the thrust experienced by the bottom and the vertical sides of the tank filled with water.
Step 1: Calculate the thrust on the bottom of the tank
1. Determine the area of the bottom of the tank:
The tank has a square cross-section with dimensions 2m×2m.
Area=length×width=2m×2m=4m2
2. Calculate the pressure at the bottom of the tank:
The pressure at the bottom of the tank can be calculated using the formula:
P=h⋅ρ⋅g
where:
- h=2.5m (height of water)
- ρ=1000kg/m3 (density of water)
- g=10m/s2 (acceleration due to gravity)
Substituting the values:
P=2.5m⋅1000kg/m3⋅10m/s2=25000Pa(Pascals)
3. Calculate the thrust on the bottom of the tank:
Thrust (F) is given by:
F=P⋅A
Substituting the values:
F=25000Pa⋅4m2=100000N
Step 2: Calculate the thrust on the vertical sides of the tank
1. Determine the thrust on one vertical side:
The vertical side has a height of 2.5m and a width of 2m. We can divide the vertical surface into horizontal strips of height dx.
2. Calculate the pressure at a depth y:
The pressure at a depth y is given by:
P(y)=y⋅ρ⋅g
3. Calculate the thrust on a strip of height dx:
The area of the strip is:
dA=2m⋅dx
The thrust on the strip is:
dF=P(y)⋅dA=(y⋅ρ⋅g)⋅(2dx)
Substituting the values:
dF=(y⋅1000⋅10)⋅(2dx)=20000ydx
4. Integrate to find the total thrust on the vertical side:
The total thrust Fv on the vertical side from y=0 to y=2.5m is:
Fv=∫2.5020000ydy
Evaluating the integral:
Fv=20000(y22)2.50=20000⋅(2.5)22=20000⋅6.252=20000⋅3.125=62500N
Final Results
- Thrust on the bottom of the tank: 100000N
- Thrust on the vertical side of the tank: 62500N
The tank has a square cross-section with dimensions 2m×2m.
Area=length×width=2m×2m=4m2
The pressure at the bottom of the tank can be calculated using the formula:
P=h⋅ρ⋅g
where:
- h=2.5m (height of water)
- ρ=1000kg/m3 (density of water)
- g=10m/s2 (acceleration due to gravity)
P=2.5m⋅1000kg/m3⋅10m/s2=25000Pa(Pascals)
Thrust (F) is given by:
F=P⋅A
Substituting the values:
F=25000Pa⋅4m2=100000N
The vertical side has a height of 2.5m and a width of 2m. We can divide the vertical surface into horizontal strips of height dx.
The pressure at a depth y is given by:
P(y)=y⋅ρ⋅g
The area of the strip is:
dA=2m⋅dx
The thrust on the strip is:
dF=P(y)⋅dA=(y⋅ρ⋅g)⋅(2dx)
Substituting the values:
dF=(y⋅1000⋅10)⋅(2dx)=20000ydx
The total thrust Fv on the vertical side from y=0 to y=2.5m is:
Fv=∫2.5020000ydy
Evaluating the integral:
Fv=20000(y22)2.50=20000⋅(2.5)22=20000⋅6.252=20000⋅3.125=62500N
- Thrust on the bottom of the tank: 100000N
- Thrust on the vertical side of the tank: 62500N
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
An observer observer a fish moving upwards in a cylindrical container of cross section area 1m2 filled with water up to a height of 5m. A hole is present at the botton of the container having cross section areea 1/1000m2. Find out the speed of the image of fish observed by observer when the botton hole is just opened. (Given: The fish is moving with the speed of 6m/s towards the observer, μ of water =4/3)
View SolutionA tank of large base area is filled with water up to a height of 5m. A hole of 2cm2 cross section in the bottom allows the water to drain out in continuous streams. For this situation, mark out the correct statement(s) (take ρwater=1000kg/m3,g=10ms−12)

View SolutionThe wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=0)
 ,
,
View SolutionA ball is projected vertically up wards with a velocity of 100 m/s. Find the speed of the ball at half the maximum height. (g=10m/s2)
View SolutionA ball is thrown up at a speed of 4.0 m/s. Find the maximum height reached by the ball. Take g=10m/s2.
View Solution
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionA ball is projected vertically up with speed 20 m/s. Take g=10m/s2
View SolutionA tank of base area 4m2 is initially filled with water up to height 2m. An object of uniform cross-section 2m2 and height 1m is now suspended by wire into the tank, keeping distance between base of tank and that of object 1m. Density of the object is 2000kg/m3. Take atmospheric pressure 1×105N/m2,g=10m/s2.
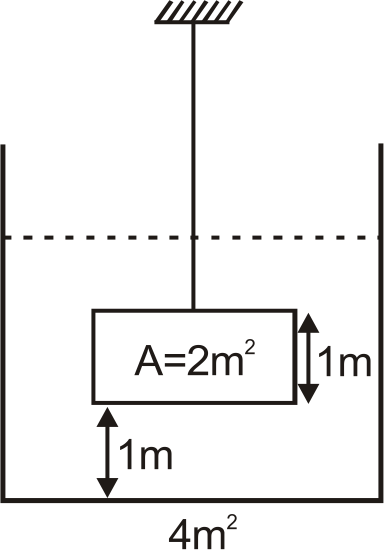
The downwards force exerted by the water on the top surface of the object is
View SolutionA tank of base area 4m2 is initially filled with water up to height 2m. An object of uniform cross-section 2m2 and height 1m is now suspended by wire into the tank, keeping distance between base of tank and that of object 1m. Density of the object is 2000kg/m3. Take atmospheric pressure 1×105N/m2,g=10m/s2.
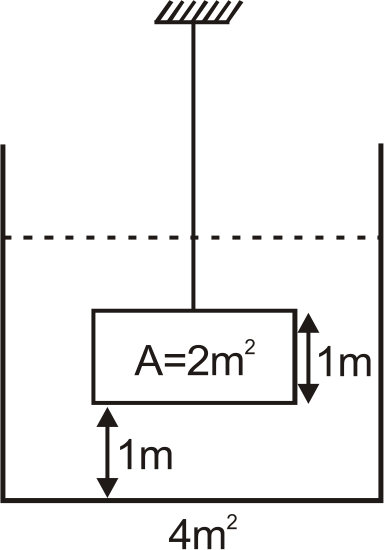
The tension in the wire is
View SolutionA tank of base area 4m2 is initially filled with water up to height 2m. An object of uniform cross-section 2m2 and height 1m is now suspended by wire into the tank, keeping distance between base of tank and that of object 1m. Density of the object is 2000kg/m3. Take atmospheric pressure 1×105N/m2,g=10m/s2.
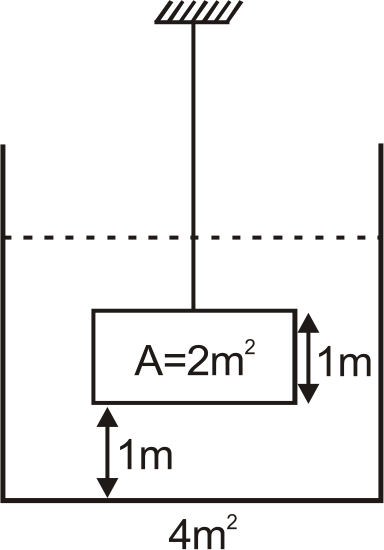
The buyont force on the object is
View Solution
