A U-tube rotates with angular velocity ω about the vertical axis AB. What is the difference in fluid level h in terms of ω the radii r1 and r2 and the fluid density ρ?
To solve the problem of finding the difference in fluid level h in a rotating U-tube in terms of angular velocity ω, the radii r1 and r2, and the fluid density ρ, we can follow these steps:
Step 1: Understand the System
The U-tube is rotating about a vertical axis, which means that the fluid inside the U-tube experiences a centripetal acceleration due to the rotation. The pressure in a fluid at rest increases with depth, but in this case, we need to consider the effect of rotation.
Step 2: Determine the Centripetal Acceleration
The centripetal acceleration ac at a distance r from the axis of rotation is given by:
ac=ω2r
This acceleration acts towards the center of the circular path.
Step 3: Relate Pressure Change to Centripetal Acceleration
The change in pressure dp due to the centripetal acceleration when moving a small distance dr can be expressed as:
dp=−ρacdr=−ρω2rdr
The negative sign indicates that pressure decreases as we move outward from the axis of rotation.
Step 4: Integrate to Find Pressure Difference
To find the pressure difference P2−P1 between two points at radii r1 and r2, we integrate the expression for dp:
P2−P1=∫r2r1−ρω2rdr
Calculating the integral:
P2−P1=−ρω2(r22)r2r1=−ρω2(r222−r212)=−ρω22(r22−r21)
Step 5: Relate Pressure Difference to Height Difference
The pressure difference can also be related to the height difference h in the fluid columns:
P2−P1=ρg(h2−h1)=ρgh
where h=h2−h1 is the height difference we want to find.
Step 6: Set the Equations Equal
Equating the two expressions for pressure difference:
ρgh=−ρω22(r22−r21)
Since we are interested in the magnitude of the height difference, we can write:
h=ω22g|r22−r21|
Final Answer
Thus, the difference in fluid level h in terms of ω, r1, r2, and ρ is:
h=ω22g|r22−r21|
The U-tube is rotating about a vertical axis, which means that the fluid inside the U-tube experiences a centripetal acceleration due to the rotation. The pressure in a fluid at rest increases with depth, but in this case, we need to consider the effect of rotation.
The centripetal acceleration ac at a distance r from the axis of rotation is given by:
ac=ω2r
This acceleration acts towards the center of the circular path.
The change in pressure dp due to the centripetal acceleration when moving a small distance dr can be expressed as:
dp=−ρacdr=−ρω2rdr
The negative sign indicates that pressure decreases as we move outward from the axis of rotation.
To find the pressure difference P2−P1 between two points at radii r1 and r2, we integrate the expression for dp:
P2−P1=∫r2r1−ρω2rdr
Calculating the integral:
P2−P1=−ρω2(r22)r2r1=−ρω2(r222−r212)=−ρω22(r22−r21)
The pressure difference can also be related to the height difference h in the fluid columns:
P2−P1=ρg(h2−h1)=ρgh
where h=h2−h1 is the height difference we want to find.
Equating the two expressions for pressure difference:
ρgh=−ρω22(r22−r21)
Since we are interested in the magnitude of the height difference, we can write:
h=ω22g|r22−r21|
Thus, the difference in fluid level h in terms of ω, r1, r2, and ρ is:
h=ω22g|r22−r21|
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Solved Examples
Explore 7 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Exercise 4.1
Explore 11 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A rod is rotating with angular velocity ω about axis AB. Find cosθ.

View SolutionThere are two blocks of masses m1 and m2,m1 is placed on m2 on a table which is rotating with an angular velocity ω about the vertical axis . The coefficent of friction between the block is μ1 and between m2 and table is μ2(μ1<μ2) if block are placed at distance R from the axis of ratation , for relative sliding between the surface in contact , find the
a. friction force at the contacting surface
b. maximum angular speed ω

View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA rough horizontal plate rotates with angular velocity ω about a fixed vertical axis. A particle or mass m lies on the plate at a distance 5a4 from this axis. The coefficient of friction between the plate and the particle is 13 . The largest value of ω2 for which the particle will continue to be at rest on the revolving plate is
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -

View SolutionA horizontally orientd tube of length l rotates with a constant angular velocity ω about a stationary vertical axis. XX passing through end A. The tube is filled with ideal fluid.
The end A of tube is having pressure P0. The closed end B has a small hole and at time t = 0, the fluid column has length of l. Find velocity of fluid relative to tube at the instant t = 0

View SolutionA U tube is rotated about one of it's limbs with an angular velocity ω. Find the difference in height H of the liquid (density ρ) level, where diameter of the tube d<<L.
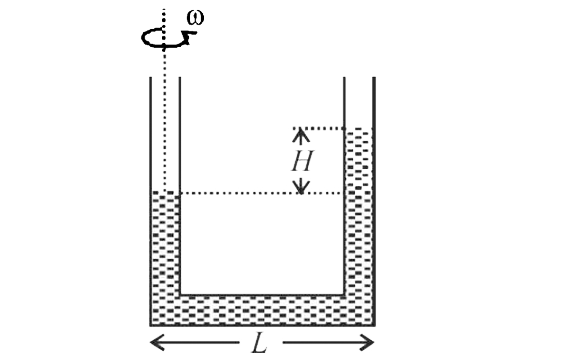
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View Solution