The end of a capillary tube with a radius r is immersed in water. Is mechanical energy conserved when the water rises in the tube? The tube is suficiently long. If not calculate the energy change.
To determine whether mechanical energy is conserved when water rises in a capillary tube, we can analyze the forces and energy changes involved in the process. Here’s a step-by-step solution:
Step 1: Understand the Forces Involved
When the capillary tube is immersed in water, the water rises due to the balance between the surface tension force and the weight of the water column inside the tube. The surface tension force (Fs) can be expressed as:
Fs=γ⋅L
where γ is the surface tension and L is the length of the contact line, which for a circular tube is 2πr.
Step 2: Calculate the Weight of the Water Column
The weight (W) of the water column that rises to a height h in the tube can be calculated as:
W=ρ⋅V⋅g=ρ⋅(πr2h)⋅g
where ρ is the density of water and g is the acceleration due to gravity.
Step 3: Set Up the Equilibrium Condition
At equilibrium, the upward force due to surface tension equals the downward force due to the weight of the water column:
Fs=W
Substituting the expressions from Steps 1 and 2:
γ⋅(2πr)=ρ⋅(πr2h)⋅g
Step 4: Solve for Height h
Rearranging the equation gives:
h=2γρgr
Step 5: Calculate Work Done by Surface Tension
The work done (W_s) by the surface tension force when the water rises to height h is:
Ws=Fs⋅h=γ⋅(2πr)⋅h
Substituting h from Step 4:
Ws=γ⋅(2πr)⋅(2γρgr)=4γ2πρg
Step 6: Calculate the Change in Potential Energy
The change in potential energy (PE) of the water column when it rises to height h is:
PE=W⋅h2=(ρ⋅(πr2h)⋅g)⋅h2
Substituting h:
PE=(ρ⋅πr2⋅2γρgr)⋅g⋅2γρg⋅12
Simplifying gives:
PE=2γ2πρg
Step 7: Determine the Energy Change
The energy change (loss of energy) can be calculated as:
Energy Loss=Ws−PE
Substituting the values from Steps 5 and 6:
Energy Loss=4γ2πρg−2γ2πρg=2γ2πρg
Conclusion
Mechanical energy is not conserved when the water rises in the capillary tube. The energy loss is given by:
Energy Loss=2γ2πρg
When the capillary tube is immersed in water, the water rises due to the balance between the surface tension force and the weight of the water column inside the tube. The surface tension force (Fs) can be expressed as:
Fs=γ⋅L
where γ is the surface tension and L is the length of the contact line, which for a circular tube is 2πr.
The weight (W) of the water column that rises to a height h in the tube can be calculated as:
W=ρ⋅V⋅g=ρ⋅(πr2h)⋅g
where ρ is the density of water and g is the acceleration due to gravity.
At equilibrium, the upward force due to surface tension equals the downward force due to the weight of the water column:
Fs=W
Substituting the expressions from Steps 1 and 2:
γ⋅(2πr)=ρ⋅(πr2h)⋅g
Rearranging the equation gives:
h=2γρgr
The work done (W_s) by the surface tension force when the water rises to height h is:
Ws=Fs⋅h=γ⋅(2πr)⋅h
Substituting h from Step 4:
Ws=γ⋅(2πr)⋅(2γρgr)=4γ2πρg
The change in potential energy (PE) of the water column when it rises to height h is:
PE=W⋅h2=(ρ⋅(πr2h)⋅g)⋅h2
Substituting h:
PE=(ρ⋅πr2⋅2γρgr)⋅g⋅2γρg⋅12
Simplifying gives:
PE=2γ2πρg
The energy change (loss of energy) can be calculated as:
Energy Loss=Ws−PE
Substituting the values from Steps 5 and 6:
Energy Loss=4γ2πρg−2γ2πρg=2γ2πρg
Mechanical energy is not conserved when the water rises in the capillary tube. The energy loss is given by:
Energy Loss=2γ2πρg
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Solved Examples11videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.112videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
Similar Questions
Figure shows a capillary tube of radius r dipped into water. If the atmosphere pressure is P0, the pressure at point A is
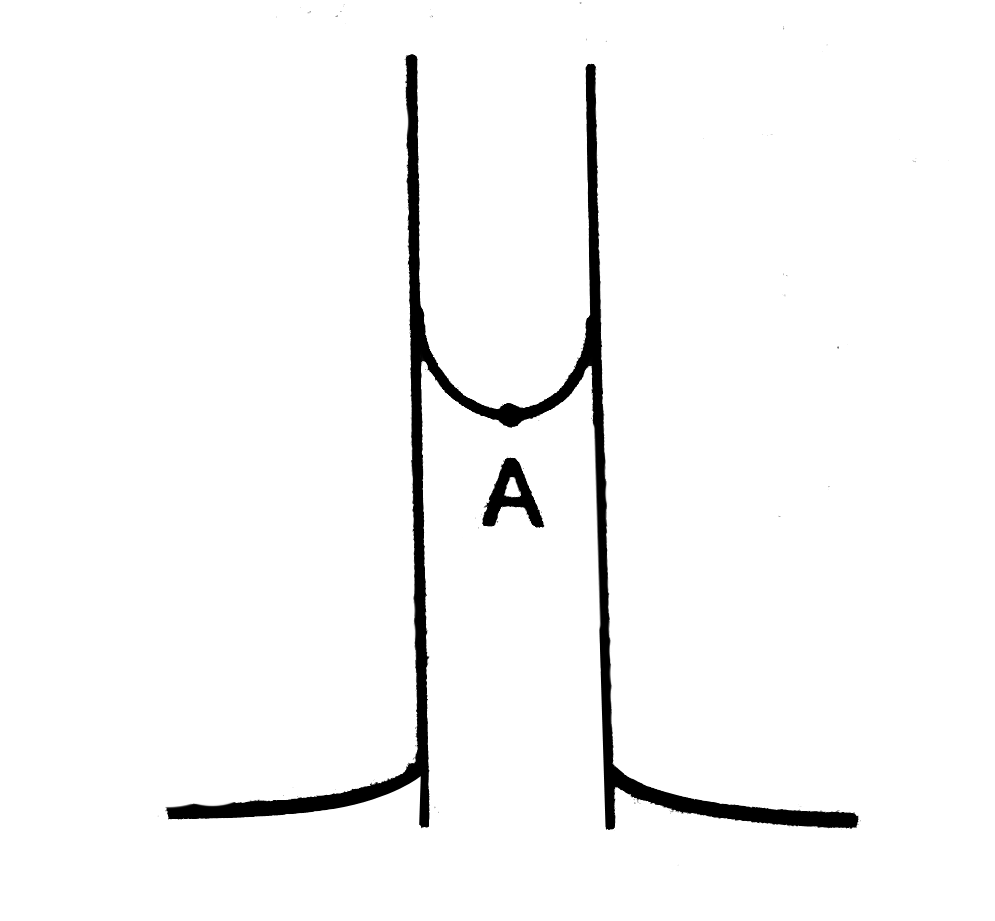 View Solution
View SolutionIf a capillary tube of radius 1 mm is immersed in water , the mass of water rising in the capillary tube is M . If the radius tube is doubled , then the mass of water , that rises in the capillary tube will be
View Solution
Knowledge Check
- Question 1 - Select One
A capillary tube of radius r is immersed in water and water rises in to a height h. The mass of water in the capillary tube is 5g. Another capillary tube of radius 2 r is immersed in water. The mass of water that will rise in this tube is
A2.5 gB5.0 gC10 gD20 g
Water rises upto 10 cm height in a long capillary tube. If this tube is immersed in water so that the height above the water surface is only 8 cm, then
View SolutionOne end of a glass capillary tube with a radius r=0.05cm is immersed into water to a depth of h=2cm.Excess pressure required to blow an air bubble out of the lower end of the tube will be (S.T of water =70dyne/cm).Take g=980cm/s2.
View SolutionA capillary tube of the radius r is immersed in water and water rise in it to a height H. Mass of water in the capillary tube is m. If the capillary of radius 2r is taken and dipped in water, the mass of water that will rise in the capillary tube will be
View SolutionThe end of a capillary tube is immersed into a liquid. Liquid slowly rises in the tube up to some height. The capillary-fluid system
View SolutionWater rises to a height h when a capillary of radius r is dipped in water. For another capillary of radius 2r dipped in water, it rises to the height
View SolutionA glass capillary tube of internal radius r=0.25mm is immersed in water. The top end of the tube projects by 2cm above the surface of water. At what angle does the liquid meet the tube? Surface tension of water =0.7Nm−1.
View SolutionA uniform capillary tube of inner radius r is dipped vertically into a beaker filled with water. The water rises to a height h in the capillary tube above the water surface in the beaker. The surface tension of water is σ. The angle of contact between water and the wall of the capillary tube is θ. Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
View Solution

