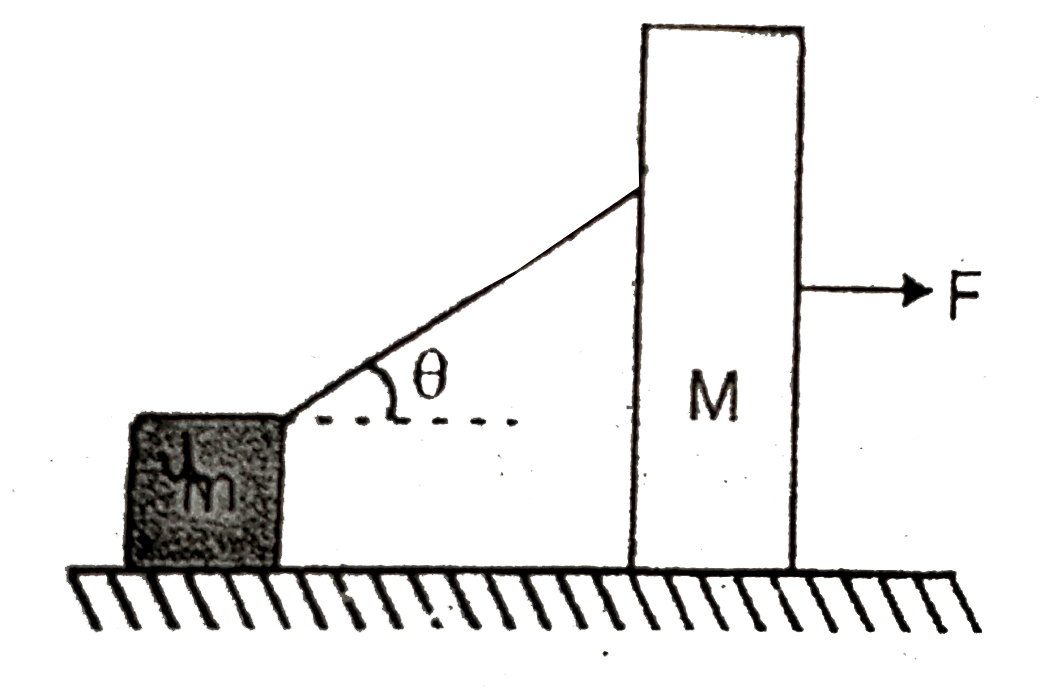
The ratio of tensions in the string connected to the block of mass m2 in figure, respectively, is (friction is absent everywhere):[m1=50kg,m2=80kg and F=1000N]
![The ratio of tensions in the string connected to the block of mass m(2) in figure, respectively, is (friction is absent everywhere):[m(1)=50 kg, m(2)=80kg and F=1000N]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_VOL2_CA1_E01_011_Q01.png)
7:2
2:7
3:4
4:3
The correct Answer is:C
In fig a in the question let tension in the string be T1.
F−T1=m1a
⇒1000−T1=50a…………i
T1−m2=m2a
⇒T1−80g=80a………..ii
From eqn i and i T1=1200013N
In fi b, in the equation, let tension in the string be T2
F+m1g−T2=m1a
⇒1000+50g=T2=50a...........iii
T2=80g=80a............iv
From eqn iii and iv we get
T2=1600013N⇒T1T2=1200016000=34
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
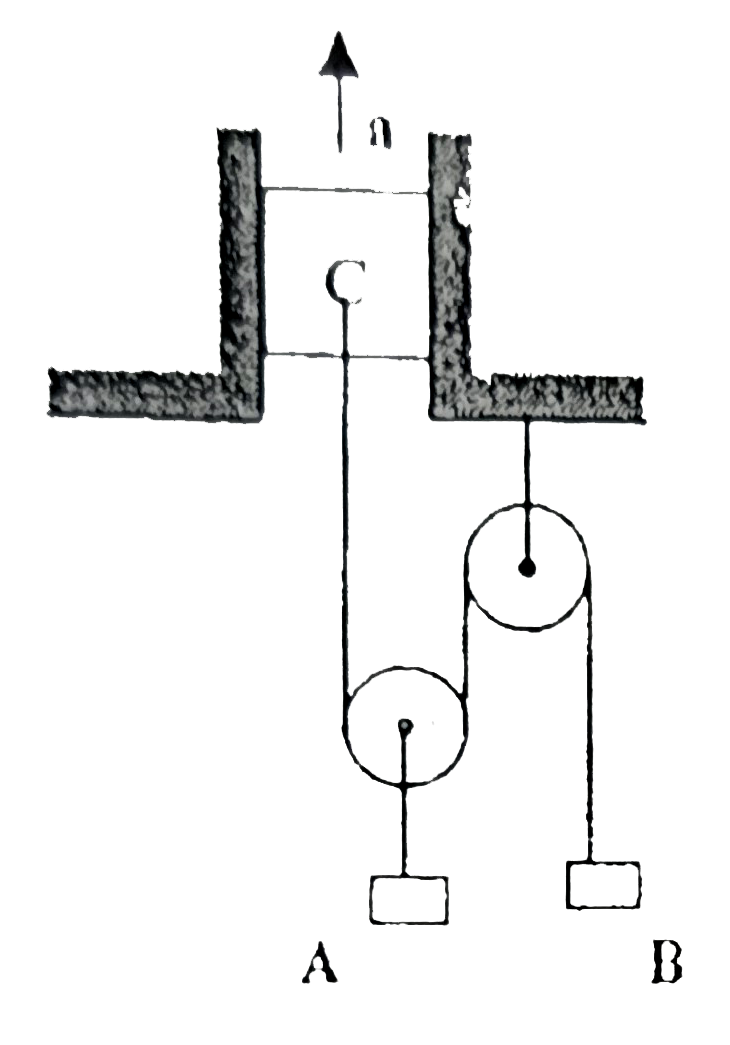
Find the mass M so that it remains at rest in the abjoining figure. Both the pulley and string are light and friction is absent everywhere. (g=10m/s2)

View SolutionThe block C shown in the figure is ascending with an acceleration a=3m/s2 by means of some motor not shown here. Find the acceleration of the bodies A and B of masses 10kg and 5kg respectively in m/s2, assuming pulleys are massless and friction is absent everywhere.
View SolutionA block of mass 'm' is raised by a man of mass m2 in two different ways as shown (m1=25kg,m2=50kg)
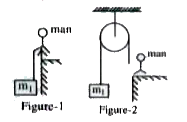
View SolutionTwo blocks of masses m and M are connected by an inextensible light string as shown in the figure. When a constant horizontal force F acts on the block of the mass M, then tension in the string is : (Assume that constact between the ground and the two blocks are frictionless) and blocks will not topple. (Given: m=1kg,M=4kg,F=10N,θ=60∘)
View SolutionThree blocks are connected as shown in fig. on a horizontal frictionless table if m1=1kg,m2=8kg,m3=27kg and T3=36N,T2 will be:-

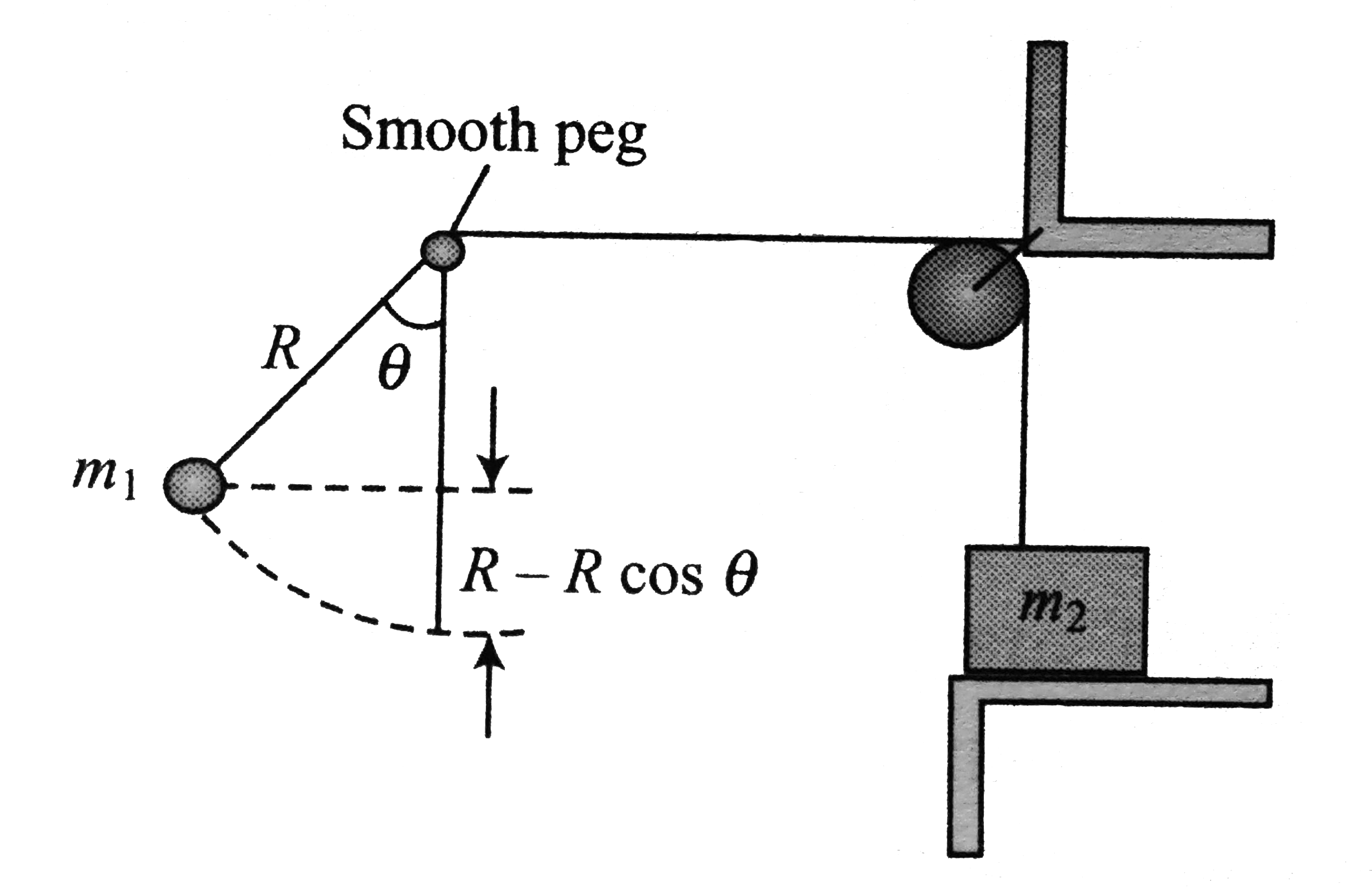
View SolutionTwo blocks are connected by a massless string that passes over a frictionless peg as shown in figure. One end of the string is attached to a mass m1=3kg, i.e., a distance R=1.20m from the peg. The other end of the string is connected to a block of mass m2=6kg resting on a table. From what angle θ, measured from the vertical, must the 3−kg block be released in order to just lift the 6kg block off the table?
View SolutionIf the system shown in the figure is rotated in a horizontal circle with angular velocity ω . Find (g=10m/s2)
(a) the minimum value of ω to start relative motion between the two blocks.
(b) tension in the string connecting m1 and m2 when slipping just starts between the blocks
The coefficient of frition between the two masses is 0.5 and there is no friction between m2 and ground. The dimensions of the masses can be neglected. (Take R=0.5m,m1=2Kg,m2=1Kg)

View SolutionA block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is
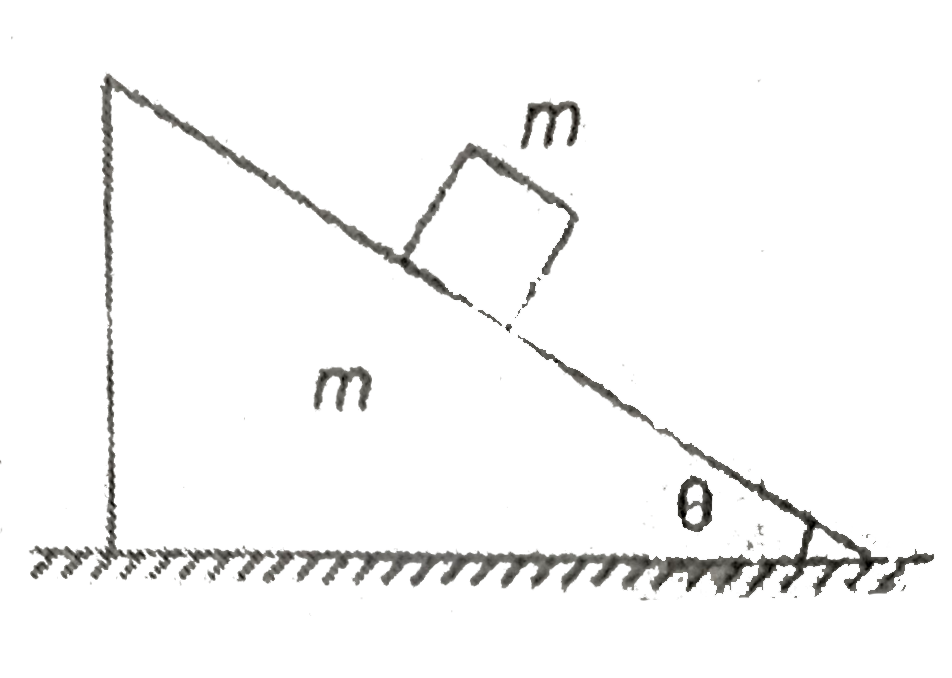
View SolutionA block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is

View SolutionThree blocks are arranged on a horizontal table ABCD as shown in the figure . The strings and pulleys are massless and both the pulleys stand vertical . The strings connecting blocks m1andm2 are also vertical and are perpendicular to faces AB and BC which are mutually perpendicular to each other . If m1andm2 are 3 kg and 4 kg respectively. Coefficient of friction between the block m3=10kg and the surface is μ=0.6 then, frictional force on m3 is
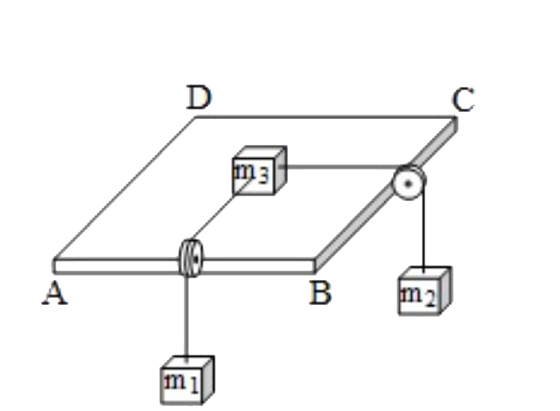
View Solution
