A block of mass m is suspended vertically with a spring of spring constant k. The block is made to oscillate in a gravitation field. Its time period is fould to be T. Now the space between the plates is made gravity free, and an electric field E is produced in the downward direction. Now the block is given a charge q. the new time period of oscillation is

T
T+2π√qEmd
2π√qEmd
none of the above
The correct Answer is:A
Time period is independent of a constant force acting on the block of spring-block system. Its time period will remain same as
T=2π√mk.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct8videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension25videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective32videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA mass m is suspended from a spring of force constant k. The period of oscillation is T0 The spring is cut into 4 equal parts: The same mass m is suspended from one of the parts. What is the new period?
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m is hanging vertically by an ideal spring of force constant K . If the mass is made to oscillate vertically, its total energy is
Amaximum at the extreme positionBmaximum at the mean positionCminimum at the mean positionDsame at all positions.
A block of mass m is connected to a spring (spring constant k). Initially the block is at rest and the spring is in its natural length. Now the system is released in gravitational field and a variable force F is applied on the upper end of the spring such that the downward acceleration of the block is given as a=g−αt, where t is time elapses and α=1m/s2, the velocity of the point of application of the force is:
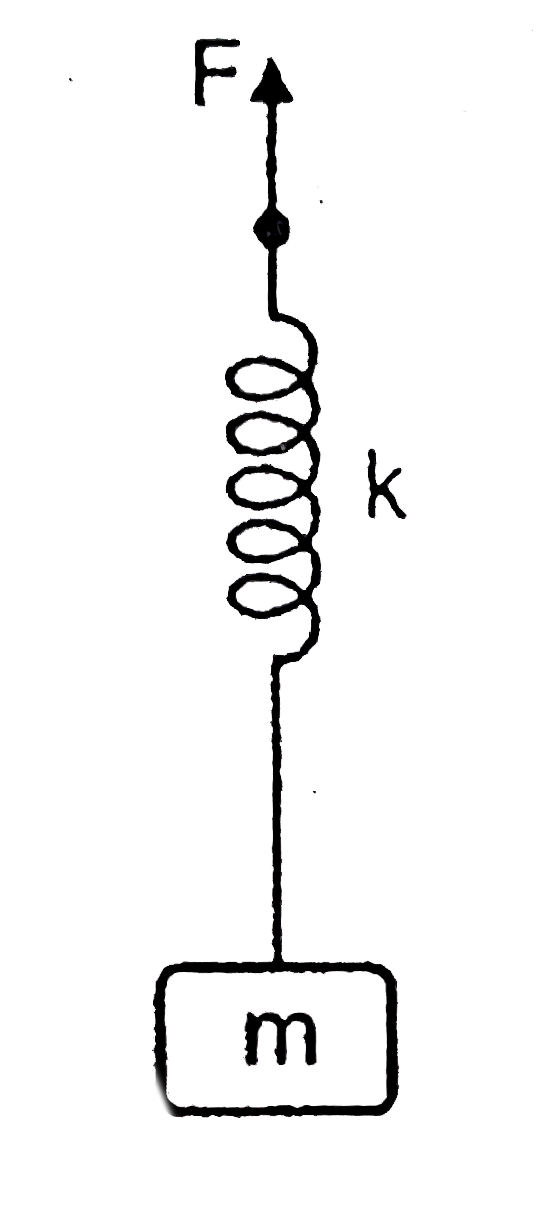 View Solution
View Solution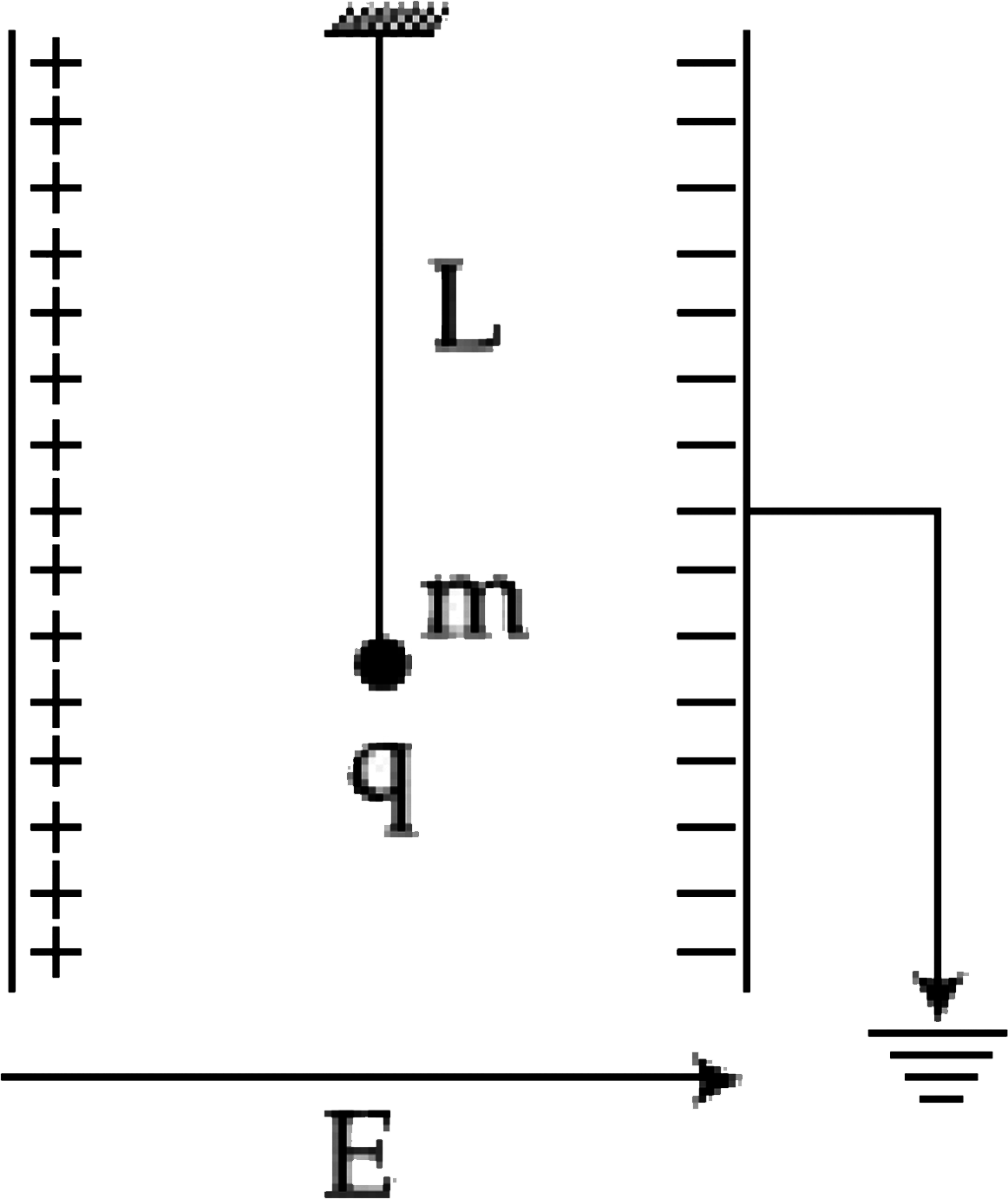
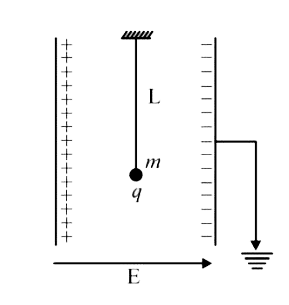
A simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:View SolutionA simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:
 View Solution
View SolutionA simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:
 View Solution
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is
 View Solution
View SolutionTime period of a block when suspended from the upper plate of a parallel plate capactor by a spring of stiffness k is when block ids unchanged If a change g is given to the block then new time period of oscilation will be
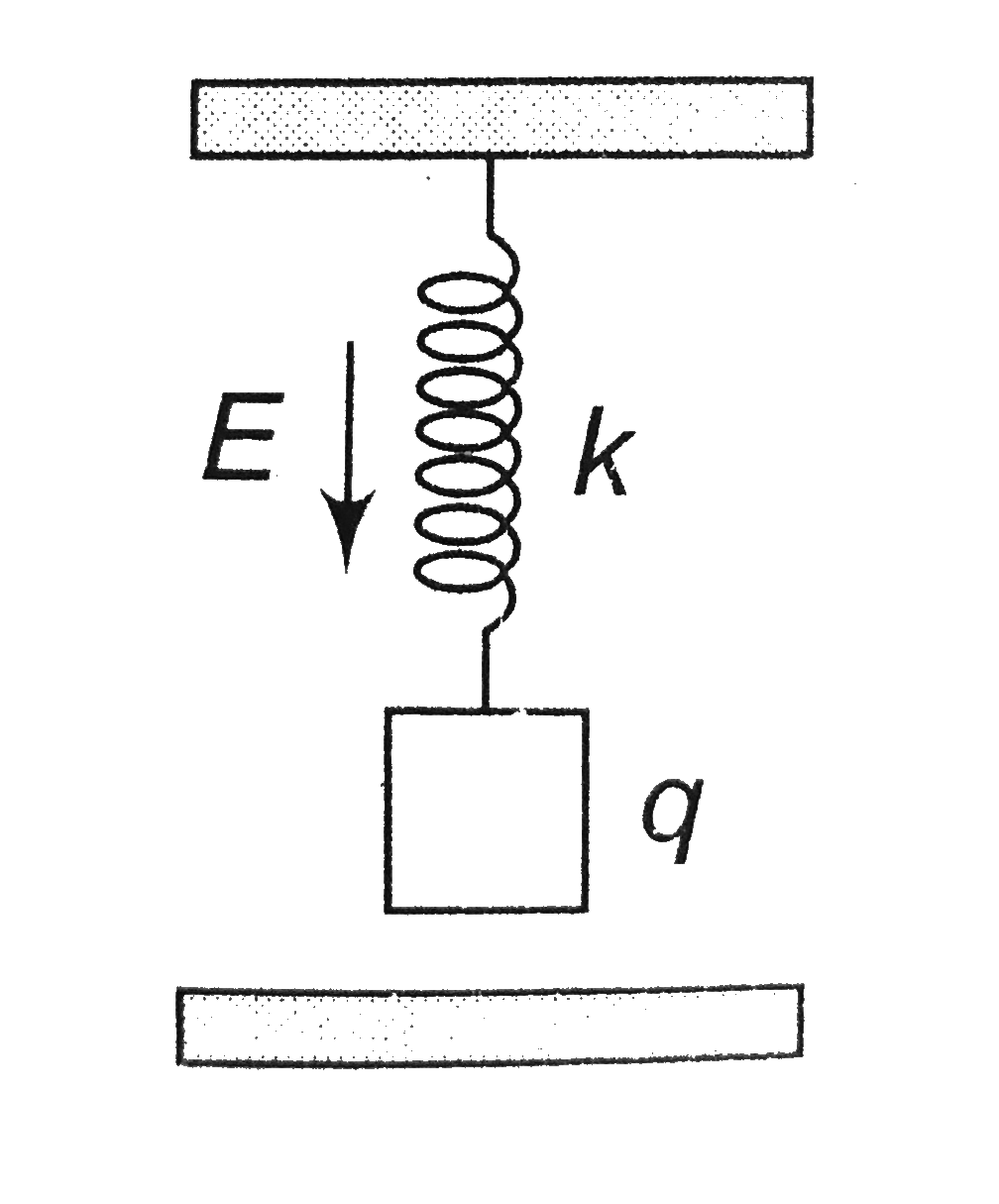 View Solution
View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 View Solution
View Solution

