Two identical metal plates each having surface area A, having charges q1andq2, are placed facing each other at a separation d. Find the charge appearing on
surface (1),(2),(3), and (4). Assume the size of the plate is much larger than the separation between the plates.
To solve the problem of finding the charge on the surfaces of two identical metal plates with charges q1 and q2 facing each other, we can follow these steps:
Step 1: Understand the Configuration
We have two parallel metal plates, each with a surface area A. The first plate has a charge q1 and the second plate has a charge q2. The plates are separated by a distance d.
Step 2: Identify the Surfaces
Label the surfaces of the plates as follows:
- Surface 1 (of Plate 1): q1−x
- Surface 2 (of Plate 1): +x
- Surface 3 (of Plate 2): −x
- Surface 4 (of Plate 2): q2+x
Step 3: Apply Charge Conservation
Since the total charge on each plate must remain constant, we can express the charges on the surfaces:
- For Plate 1: (q1−x)+x=q1
- For Plate 2: (−x)+(q2+x)=q2
Step 4: Set Up the Electric Field Equations
The electric field due to a charged plate is given by:
E=σ2ϵ0
where σ is the surface charge density and ϵ0 is the permittivity of free space.
Step 5: Write the Electric Field Contributions
The electric fields from each surface can be expressed as:
- From Surface 1: E1=(q1−x)2ϵ0A
- From Surface 2: E2=x2ϵ0A (in the opposite direction)
- From Surface 3: E3=−x2ϵ0A (in the opposite direction)
- From Surface 4: E4=(q2+x)2ϵ0A
Step 6: Set the Total Electric Field to Zero
For electrostatic equilibrium, the total electric field between the plates must be zero:
E1+E2+E3+E4=0
Substituting the expressions for the electric fields:
(q1−x)2ϵ0A−x2ϵ0A−x2ϵ0A+(q2+x)2ϵ0A=0
Step 7: Simplify the Equation
Combining the terms gives:
(q1−x−x+q2+x)2ϵ0A=0
This simplifies to:
q1−q2−x=0⟹x=q1−q2
Step 8: Calculate Charges on Each Surface
Now substituting x back into the surface charge expressions:
1. Surface 1: q1−x=q1−(q1−q2)=q2
2. Surface 2: +x=q1−q2
3. Surface 3: −x=−(q1−q2)=q2−q1
4. Surface 4: q2+x=q2+(q1−q2)=q1
Final Results
- Charge on Surface 1: q2
- Charge on Surface 2: q1−q2
- Charge on Surface 3: q2−q1
- Charge on Surface 4: q1
We have two parallel metal plates, each with a surface area A. The first plate has a charge q1 and the second plate has a charge q2. The plates are separated by a distance d.
Label the surfaces of the plates as follows:
- Surface 1 (of Plate 1): q1−x
- Surface 2 (of Plate 1): +x
- Surface 3 (of Plate 2): −x
- Surface 4 (of Plate 2): q2+x
Since the total charge on each plate must remain constant, we can express the charges on the surfaces:
- For Plate 1: (q1−x)+x=q1
- For Plate 2: (−x)+(q2+x)=q2
The electric field due to a charged plate is given by:
E=σ2ϵ0
where σ is the surface charge density and ϵ0 is the permittivity of free space.
The electric fields from each surface can be expressed as:
- From Surface 1: E1=(q1−x)2ϵ0A
- From Surface 2: E2=x2ϵ0A (in the opposite direction)
- From Surface 3: E3=−x2ϵ0A (in the opposite direction)
- From Surface 4: E4=(q2+x)2ϵ0A
For electrostatic equilibrium, the total electric field between the plates must be zero:
E1+E2+E3+E4=0
Substituting the expressions for the electric fields:
(q1−x)2ϵ0A−x2ϵ0A−x2ϵ0A+(q2+x)2ϵ0A=0
Combining the terms gives:
(q1−x−x+q2+x)2ϵ0A=0
This simplifies to:
q1−q2−x=0⟹x=q1−q2
Now substituting x back into the surface charge expressions:
1. Surface 1: q1−x=q1−(q1−q2)=q2
2. Surface 2: +x=q1−q2
3. Surface 3: −x=−(q1−q2)=q2−q1
4. Surface 4: q2+x=q2+(q1−q2)=q1
- Charge on Surface 1: q2
- Charge on Surface 2: q1−q2
- Charge on Surface 3: q2−q1
- Charge on Surface 4: q1
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Example
7 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.1
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
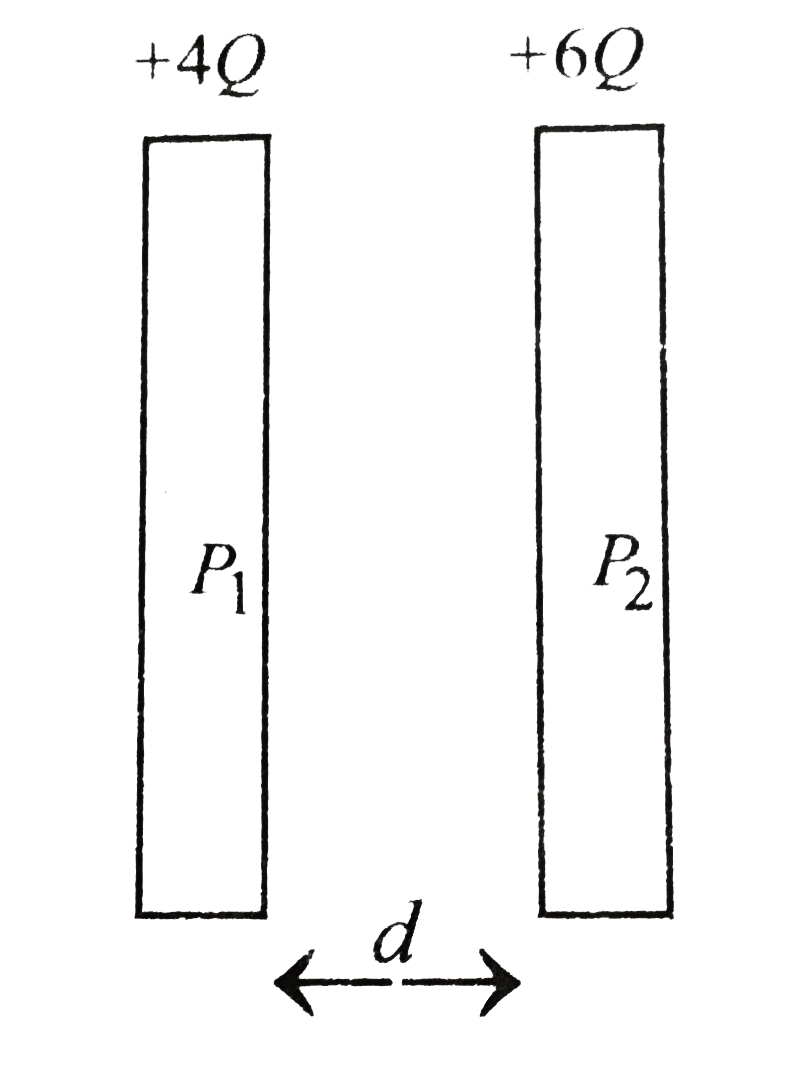
Two identical conducting very large plates P1andP2 having charges +4Qand+6Q are placed very closed to each other at separation d. The plate area of either face of the plate is A. The potential difference between plates P1andP2 is
View SolutionTwo conducting plates X and Y, each having large surface aera A (on one side), are placed parallel to each other as show in figure.

Find the surface charge density at the inner surface of the plate X.
View SolutionTwo metal plates having charges Qand−Q face each other at some separation and are dipped into an oil tank .If the oil is pumped out, the eletric field between the plates will
View SolutionTwo conducting plates M and N, each having large surface area A (on one side), are placed parallel to each other in figure. The plate M is given charge Q1 and N, charge Q2(<Q1). Then

View SolutionFigure shows an arrangement of four identical rectangular plates A,B,C, and D each of area S. Find the charges appearing on each face (from left to right) of the plates. Ignore the separation between the plates in comparison to the plate dimensions.

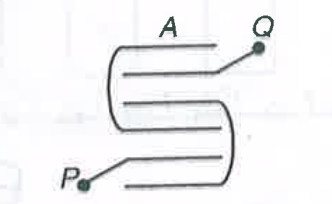
View SolutionSix identical metal plates are arranged as shown in the figure. Each plate have area A and are placed at distance d with each other. The equivalent capacitance between P and Q
View SolutionFind the equivalent capacitance between A and B.A: area of each plate, d: separation between the plates.
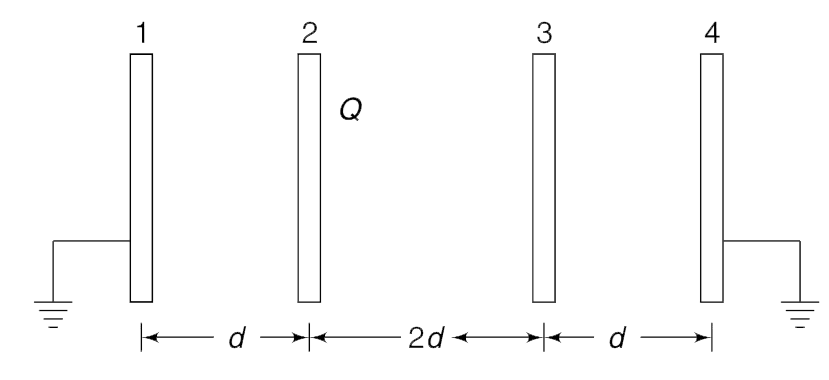
View SolutionFour large identical metallic plates are placed as shown in the Figure. Plate 2 is given a charge Q. All other plates are neutral. Now plates 1 and 4 are earthed. Area of each plate is A.
(a) Find charge appearing on right side of plate 3.
(b) Find potential difference between plates 1 and 2.
View SolutionFind the charge on each plate given area of each plate is A and separation between two consecutive plates is d.

View SolutionThe equivalent capacitance between P and Q in the figure is (area of each plate is A and separation between two consecutive plates is d)
View Solution
