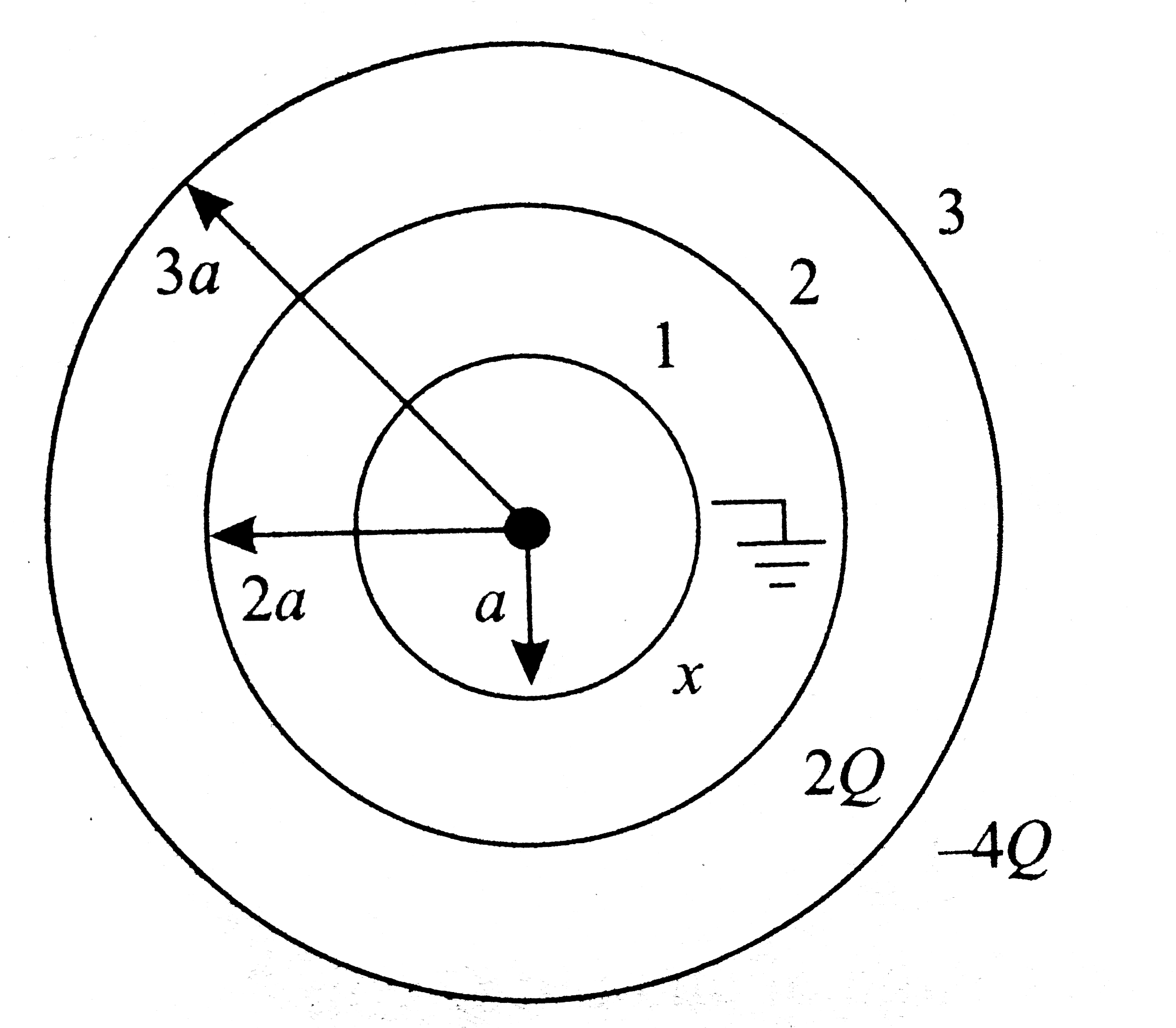
In the previous problem, if we connect the conductors 1 and 2, 2 and 3, 1 and 3, 1 and ground, 2 and ground, and 3 and ground, separately, find the charge flown in each case.
(i) If we connect the conductors 1 and 2, the potential of spheres 1 and 2 will be equal.
Here V1=V2
or Kxa+KQ−x2a+K(−4Q)3a
=Kxa+KQ−x2a+K(−4Q)3a
or x=0
The charge of sphere 1 will come to sphere 2.
Hence charge flown in this case is equal to −Q.
 .
.
(ii) If we connect the spheres 2 and 3, their potential will be same.
V2=V3
or K(−Q)2a+Kx2a+K(−2Q−x)3a
=K(−Q)3a+Kx3a+K(2Q−x)3a
or x=Q
Hence, charge of amount Q will flow from 2 to 3.
 .
.
(iii) If we 1 and 3, their potential should be equal.
V1=V3
or Kxa+K2Q2a+K(−5Q−x)3a
=Kx3a+K2Q3a+K(−5Q−x)3a
or xa−x3a=2Q3a−2Q2a
or 2xa=−Q3orx=−Q2
Hence, −Q/2 charge will flow from 1 to 3.
 .
.
(iv) Now sphere 1 is connected with ground. The potential of sphere 1 will be zero.
V1=0=Kxa+K2Q2a+K(−4Q)3a
or x=−Q+4Q3=Q3
Hence, Q+Q3=4Q3 should flow from ground to sphere.
 .
.
(v) Now sphere 2 is connected with earth. The potential sphere 2 should be zero.
V2=0=K(−Q)2a+Kx2a+K(−4Q)3a
or x2=Q2+4Q3 or x=Q+8Q3=11Q3
hence, 11Q3−2Q=5Q3 charge will flow from earth sphere.
 .
.
(vi) Now sphere 3 is connected with ground.
Here,
V3=0=K(−Q)3a+K(2Q)3a+K(x)3a
or x=Q−2Q=−Q
Hence, −3Q charge will flow from sphere to earth or 3Q charge will flow from earth to sphere.
 .
.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.3
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Knowledge Check
In the previous problem, if H1 and H2 are the maximum heights in the two cases, then
AR=2√H1H2BR=4√H1H2CR=√H21+H22DR=H1−H2
A pole 6 m high casts a shadow 2√3 m long on the ground, then find the angle of elevation of the sun.
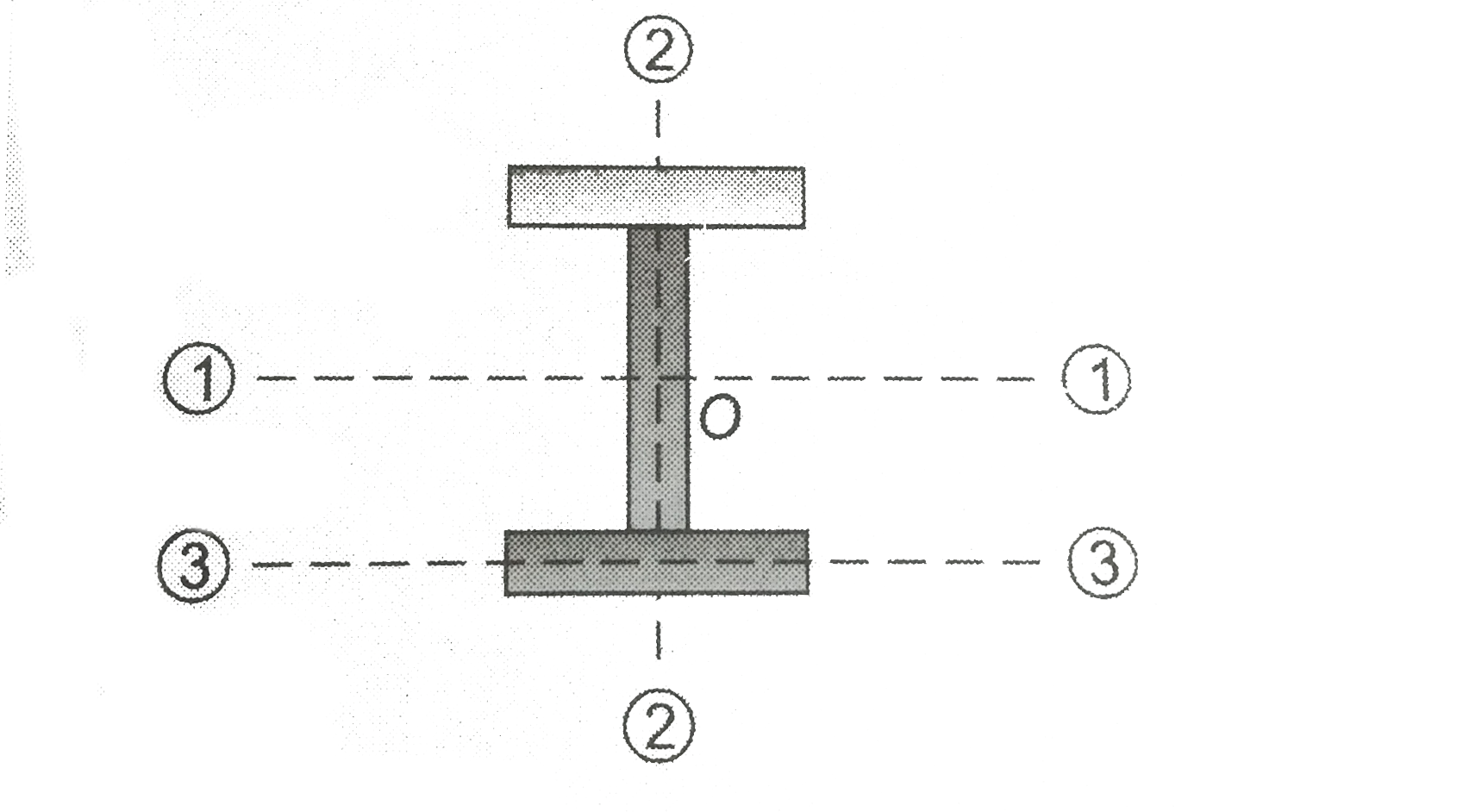
View SolutionThe three rods of the previous problem are connected symmetrically as shown. Find the M.I. about (1)−(1),(2)−(2) and (3)−(3)
View SolutionThere are two concentric metal shells of radii r1 and r2(>r1). If initially, the outer shell has a charge q and the inner shell is having zero charge and then inner shell is grounded. Find :
(i) Charge on the inner surface of outer shell.
(ii) Final charges on each sphere.
(iii) Charge flown through wire in the ground.
View SolutionThere are two concentric metal shells of radii r1 and r2(>r1). If initially, the outer shell has a charge q and the inner shell is having zero charge and then inner shell is grounded. Find :
(i) Charge on the inner surface of outer shell.
(ii) Final charges on each sphere.
(iii) Charge flown through wire in the ground.
View SolutionAB is a vertical pole with B at the ground level and A at the top. A man finds that the angle of elevation of the point A from a certain point C on the ground is 60o . He moves away from the pole along the line BC to a point D such that CD=7m . From D the angle of elevation of the point A is 45o . Then the height of the pole is (1) 7√321√3−1m (2) 7√32√3+1m (3) 7√32√3−1m (4) 7√32√3+1m
View SolutionThe ratio of the length and breadth of a tennis ground is 3:2. Find the length if the breadth is 28 metres.
View SolutionFind the charge flown through the path 1, 2, 3 as shown in figure after closing switch S and heat generated in the circuit.

View Solution
