If A is connerted with D and B is connected with C find the potential difference a across each capacitor and the final charge in each capacitor.
To solve the problem of finding the potential difference across each capacitor and the final charge in each capacitor when A is connected with D and B is connected with C, we can follow these steps:
1. Identify the Initial Conditions:
- Let the capacitance of capacitor C1 be C1=2μF and the initial voltage across it be V1=20V.
- Let the capacitance of capacitor C2 be C2=3μF and the initial voltage across it be V2=10V.
2. Calculate Initial Charges:
- The initial charge on capacitor C1 is given by:
Qi1=C1×V1=2μF×20V=40μC
- The initial charge on capacitor C2 is given by:
Qi2=C2×V2=3μF×10V=30μC
3. Consider the Polarity:
- Since the polarities of the capacitors are opposite when connected, we will consider the charge on C2 as negative:
Qi2=−30μC
4. Apply Conservation of Charge:
- The total initial charge before the connection is:
Qtotal=Qi1+Qi2=40μC−30μC=10μC
5. Determine the Common Potential (V):
- After the connection, let the common potential across both capacitors be V. The total charge after connecting the capacitors can be expressed as:
Qtotal=C1⋅V+C2⋅V
- Thus, we have:
10μC=(C1+C2)⋅V=(2μF+3μF)⋅V
- Simplifying gives:
10μC=5μF⋅V⟹V=10μC5μF=2V
6. Calculate Final Charges on Each Capacitor:
- For capacitor C1:
Qf1=C1⋅V=2μF⋅2V=4μC
- For capacitor C2:
Qf2=C2⋅V=3μF⋅2V=6μC
Final Results:
- The potential difference across each capacitor is V=2V.
- The final charge on capacitor C1 is Qf1=4μC.
- The final charge on capacitor C2 is Qf2=6μC.
- Let the capacitance of capacitor C1 be C1=2μF and the initial voltage across it be V1=20V.
- Let the capacitance of capacitor C2 be C2=3μF and the initial voltage across it be V2=10V.
- The initial charge on capacitor C1 is given by:
Qi1=C1×V1=2μF×20V=40μC
- The initial charge on capacitor C2 is given by:
Qi2=C2×V2=3μF×10V=30μC
- Since the polarities of the capacitors are opposite when connected, we will consider the charge on C2 as negative:
Qi2=−30μC
- The total initial charge before the connection is:
Qtotal=Qi1+Qi2=40μC−30μC=10μC
- After the connection, let the common potential across both capacitors be V. The total charge after connecting the capacitors can be expressed as:
Qtotal=C1⋅V+C2⋅V
- Thus, we have:
10μC=(C1+C2)⋅V=(2μF+3μF)⋅V
- Simplifying gives:
10μC=5μF⋅V⟹V=10μC5μF=2V
- For capacitor C1:
Qf1=C1⋅V=2μF⋅2V=4μC
- For capacitor C2:
Qf2=C2⋅V=3μF⋅2V=6μC
- The potential difference across each capacitor is V=2V.
- The final charge on capacitor C1 is Qf1=4μC.
- The final charge on capacitor C2 is Qf2=6μC.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Solved Examples10videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Exercise 4.113videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.315videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
Similar Questions
Find the potential difference and charge on each capacitor.
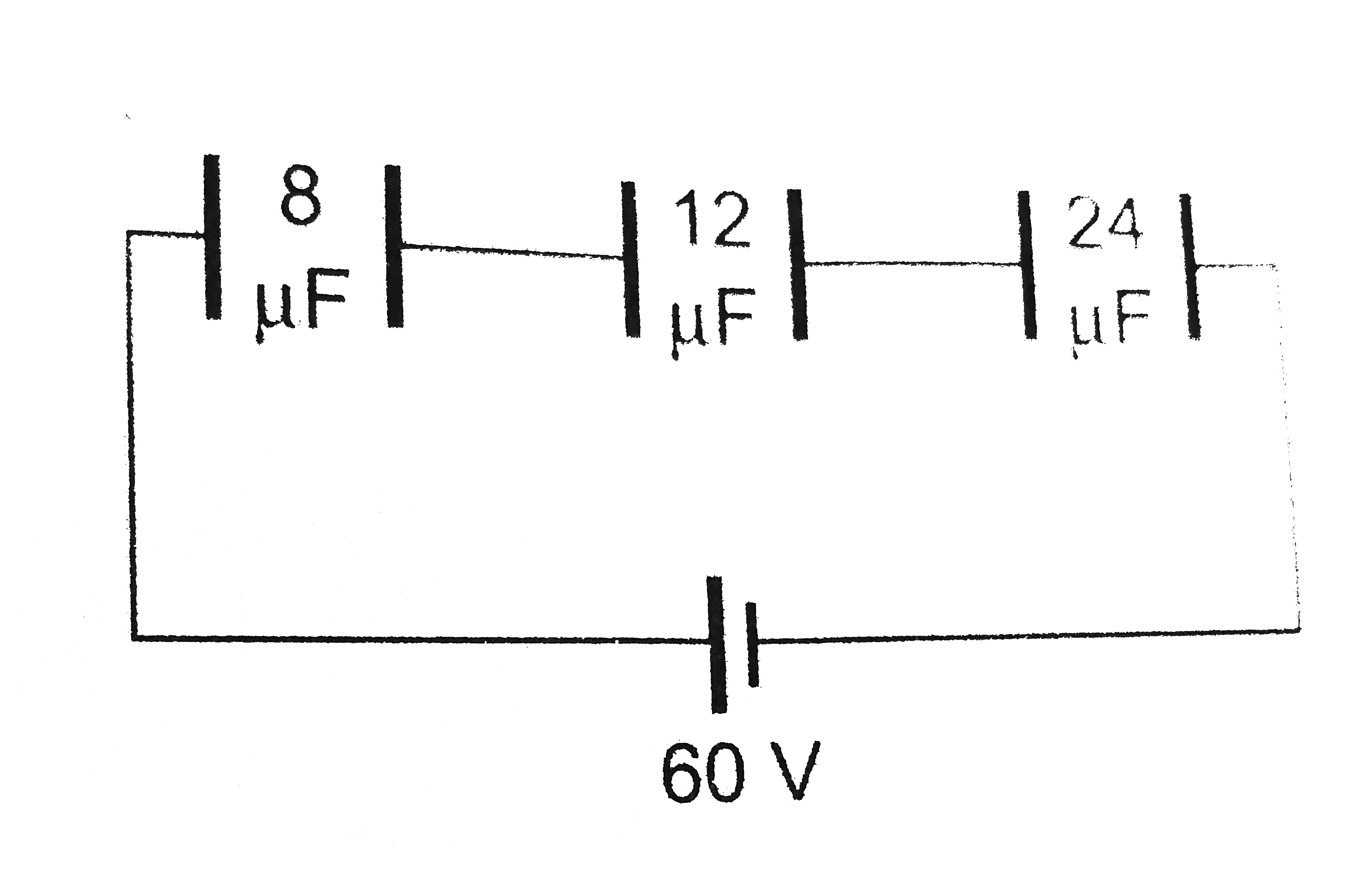 View Solution
View SolutionTwo capacitors C1 and C2 are charged 2uF AND 3uF seperately to potentials 20Vand10V, respectively. The terminals of capacitors C1andC2 are marked as (A-B) and (C-D), respectvely. A is connected with CandB is connected with D.
i. Find the final potential dsifference across each eapacitors.
ii. Find the final charge in both capacitors
iii. How much heat is produced in the circuit.View SolutionFind charge on each capacitor and potential difference across each capacitor .
 View Solution
View SolutionTwo capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View SolutionThree capacitors of capacitances 1μF,2μF, and 2μF, are cahrged up to the potential difference 30V,10V, and 15V, respectivly. If terminal A is connected with DC is connected with E and F is connected eith B, the find the charge flow in the ciruit and the final charge on the capacitors.
 . View Solution
. View SolutionThree capcitors of capacitances 4μF,
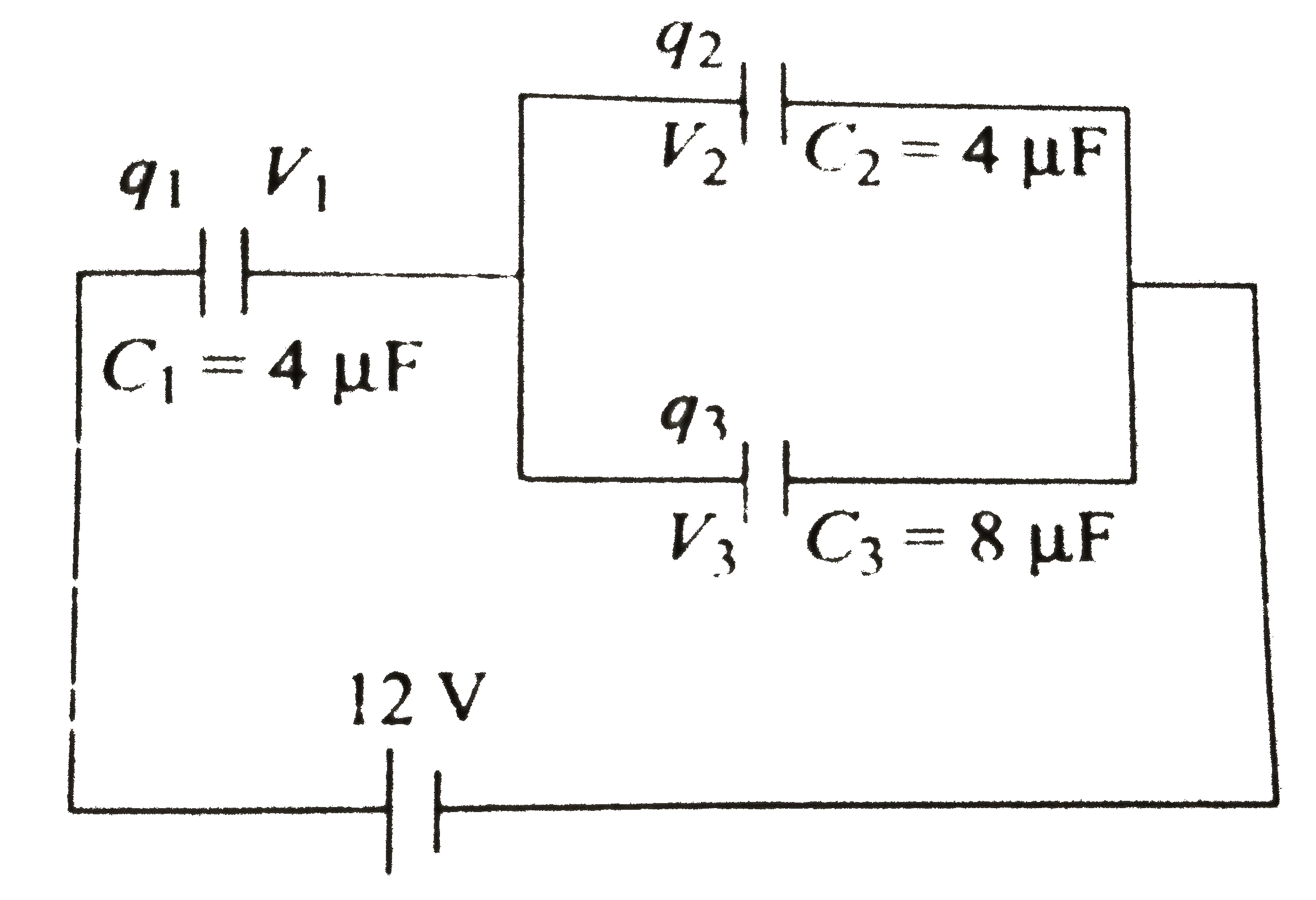 .
.
4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.View SolutionA 220 V AC supply is connected between points A and B . What will be the potential difference V across the capacitor ?
 View Solution
View SolutionA 220 V AC supply is connected between points A and B . What will be the potential difference V across the capacitor ?
 View Solution
View SolutionA 220 V AC supply is connected between points A and B . What will be the potential difference V across the capacitor ?
 View Solution
View SolutionIn the arrangement shown in , the switch S is find
 the final potential difference across the 4μF capacitorView Solution
the final potential difference across the 4μF capacitorView Solution

