Three capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emf 6V. 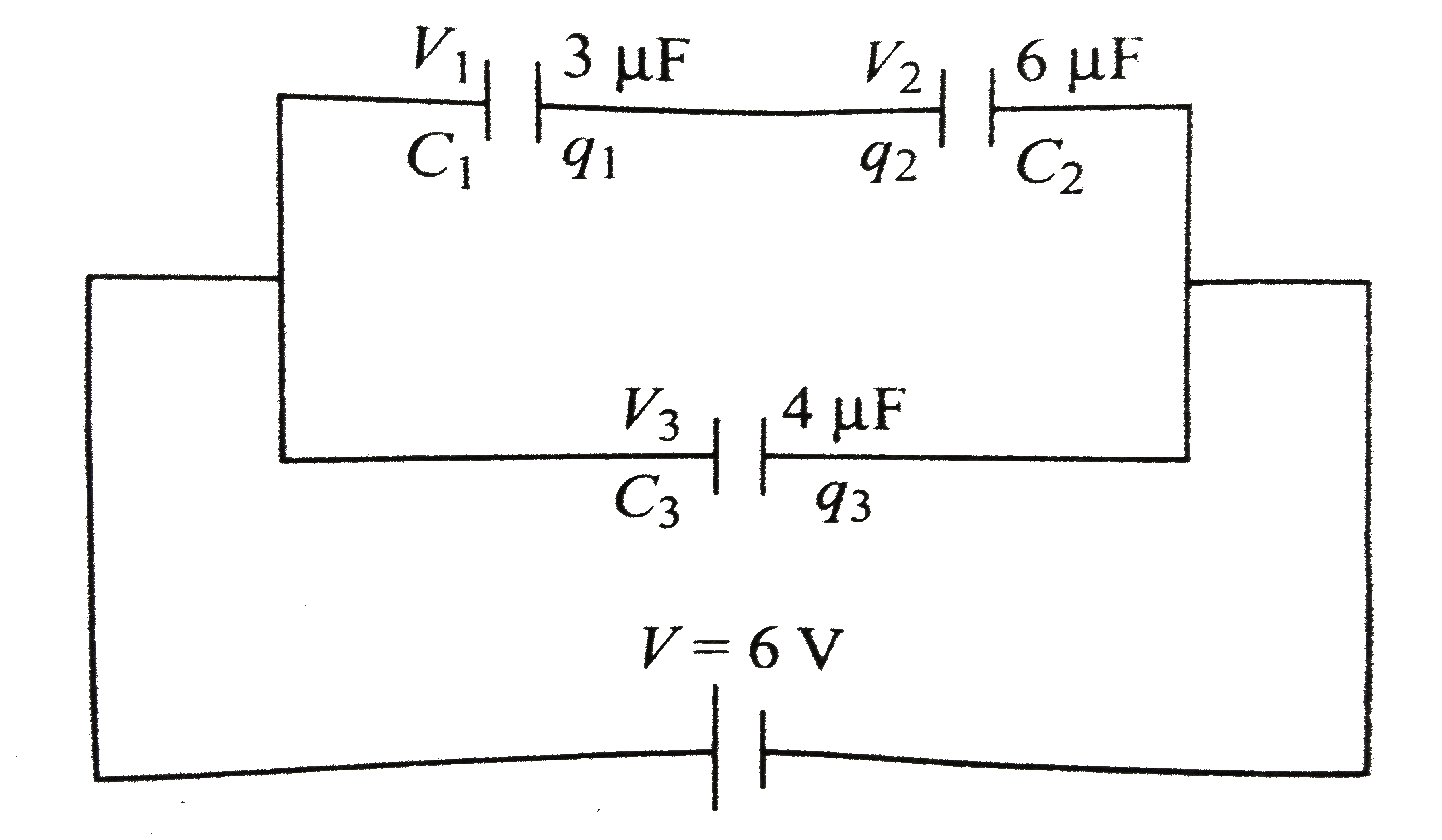 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.
i. C1 and C2 are in series, so their equivalent capacitance is
C=C1C2C1+C2=3×63+6=2μF
This C' will be in parallel C3,So<br>C_(eq)=C'+ C_(3)=2+4=6 muF<br>ii.6 Vwillbe∈paral≤lacrossC_(1)andC_(2)∈the∈verseratioofthe∩acitances.SopotentialdefferenceacrossC_(1)is<br>V_(1)=(C_(2)V)/(C_(1)+C_(2))=(6xx6)/(3+6)=4 V.<br>andpotentiald⇔ernceacrossC_(2)isV_(2)=(C_(1)V)/(C_(1)+C_(2))=(3xx6)/(3+6)=2 V<br>BecauseC_(3)isco∩ecteddirectlyarossthebaerywithoutanyother∩aci→r∈between,sopotentiald⇔erenceacrossC_(3)isV_(3) =V=6 V.Alsochar≥onC_(1)is<br>q_(1)=C_(1)V_(1)=3xx4=12 muC<br>andchar≥onC_(2)is<br>1q_(2)=C_(2)V_(2)=6xx2-12 muC<br>Weseetˆq_(1)q_(2),∵isseries,char≥isthesame.<br>chae≥onC_(3)is<br>q_(3)=C_(3)V_(3)=4xx6=24 muC.<br>A<ernativemethode→f∈dchar≥.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V03_C04_S01_016_S01.pngwh=80%mx-autosty≤=background:white;><br>Totalchar≥tˆwillflowthroughthebaeryis<br>Q = C_(eq)V = 6 xx 6 = 36 muC<br>Itwillbe÷d∫hedirectratioofC'andC_(3),so<br>q_(1) = (C'Q)/(C'+C_(3)) = (2 xx 36)/(2+4) = 12 muC<br>q_(3) = (C'Q)/(C'+C_(3)) = (4 xx 36)/(2+4) = 24 muC<br>E≠rgy∈C_(1)is<br>U_(1) = (1)/(2)C_(1)V_(1)^(2) = (1)/(2)xx3xx4 = 24mu J<br>E≠rgy∈C_(2)is<br>U_(2) = (1)/(2)C_(2)V_(2)^(2) = (1)/(2)xx6xx2^(2) = 12mu J<br>E≠rgyisC_(3)is<br>U_(3) = (1)/(2)C_(3)V_(3)^(2) = (1)/(2)xx4xx6 = 72mu J<br>Totale≠rgyis<br>U = U_(1) + U_(2) + U_(3) = 24 + 12 + 72 = 108 mu J<br>A<ernatively<br>U = (1)/(2) xx 6 xx 6^(2) = 108 muJ
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Solved Examples10videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Exercise 4.113videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.315videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
Similar Questions
Three capcitors of capacitances 4μF,
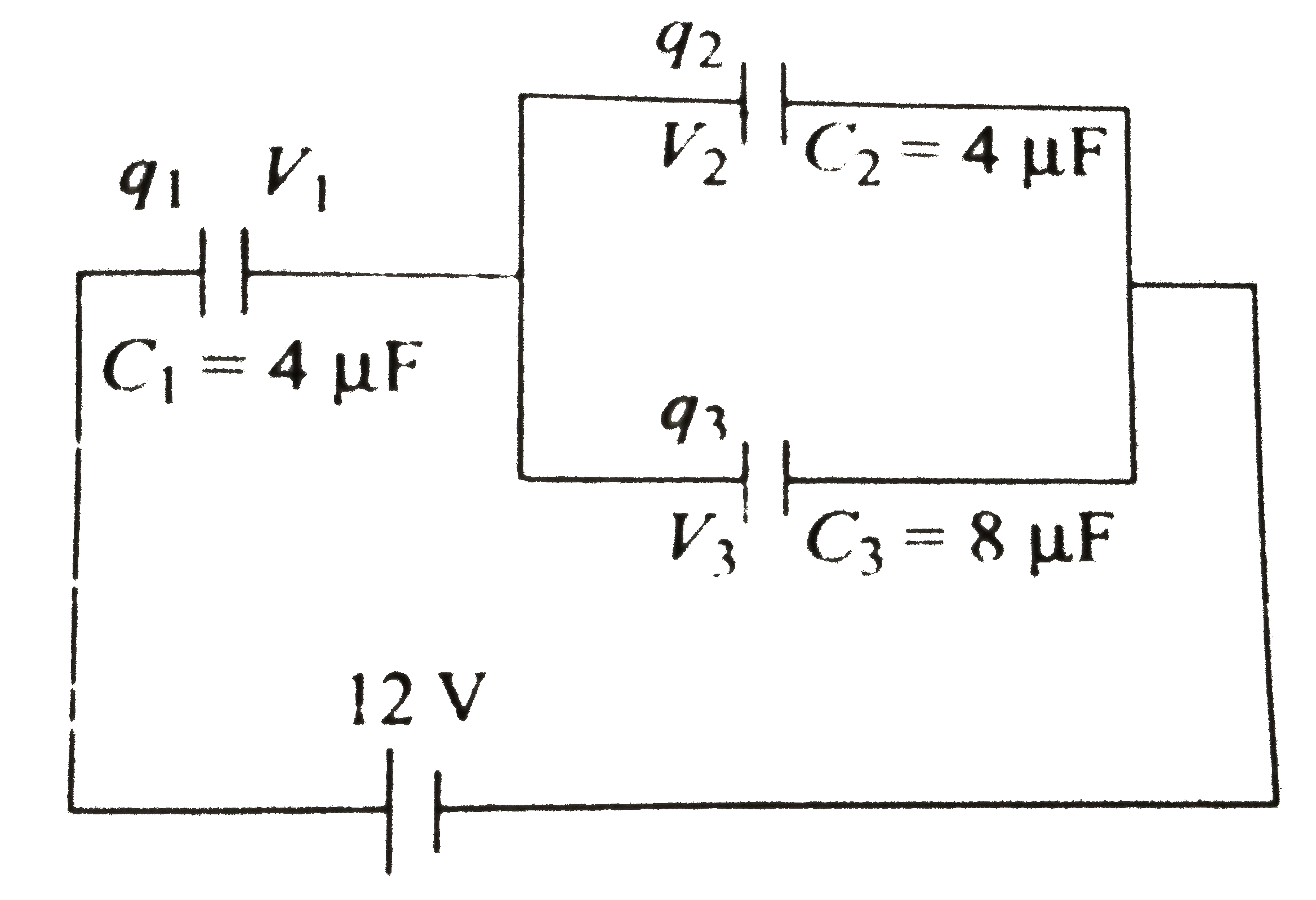 .
.
4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.View SolutionThe energy stored in 4μF capacitors is
View SolutionFind the equivalent capacitance between points A and B. Capacitance of each capacitor is 2μF.
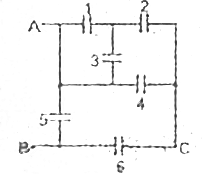 View Solution
View SolutionTwo capacitor of capacitance 4.0μFand 6.0muF' are connected in series with a battery of 20 V . Find the energy supplied by the battery .
View SolutionThree capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
View SolutionIn the circuit shown in figure find

a. the equivalent capacitance
b. the charge stored in each capacitor and
c. the potential difference across each capacitor.View SolutionIf potential difference across 3μF is 4V, then total energy stored in all capacitors is
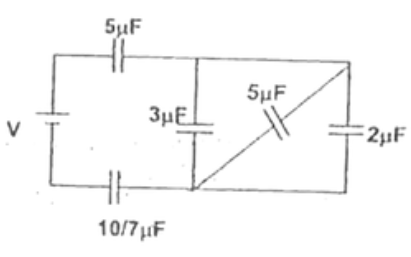 View Solution
View SolutionThree capacitors having capanctances 20μF,30μF and 40μF are conneceted in series with a 12V battary. Find the charge on each of the capacitors. How much work has been done by the battery in charging the capacitors?
View SolutionIn the circuit shown in figure 3.141, find the energy stored in 4μF capacitor in steady state.
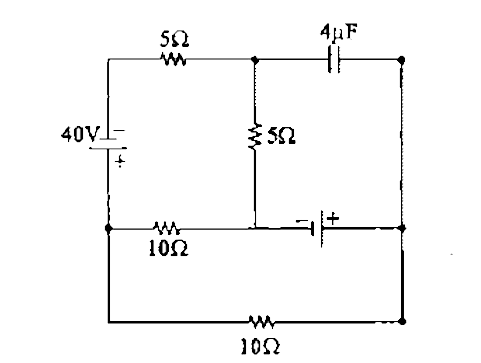 View Solution
View SolutionTwo capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View Solution


