Consider
<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V03_C04_E01_141_Q01.pngwh=80%mx-autosty≤=background:white;>.<br>Thechar≥appear∈gisC_(2) is.
E(C3C4C1+C2)
E(C1C2C1+C2)
E(C1C2C3+C4)
E(C3C4C3+C4)
The correct Answer is:B
Let charge be as shown. (Capacitors in series have the same the charge.)
Taking loop containing C1,C2, and E, we get
qC1+qC2−E=0 or q=E[C1C2C1+C2]
Similarly, from loop containing C3,C4, and E, we get
q'C3+q'C4−E=0 or q'=E[C3C4C3+C4]
Now, VA−VB=qC2−q'C
=E[C1C1+C2−C3C3+C4]
=E[C1C4−C3C2(C1+C2)(C3+C4)]
Now VA−VB=E⇒C1C4−C2C3=0
or C1C2=C3V4.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer5videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Multile Correct11videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.315videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
Similar Questions
Condsider
 .
.
Now the switch is shifted to position 2. The charge appearing on capacitor C3 isView SolutionCondsider
 .
.
The charge on capacitor C1 is.View SolutionFor the system shown in capacitance is C The left plate is given a charge Q1 and the switch is closed.
 .
.
Find the charge appearing on the inner face of the left plate.View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View Solution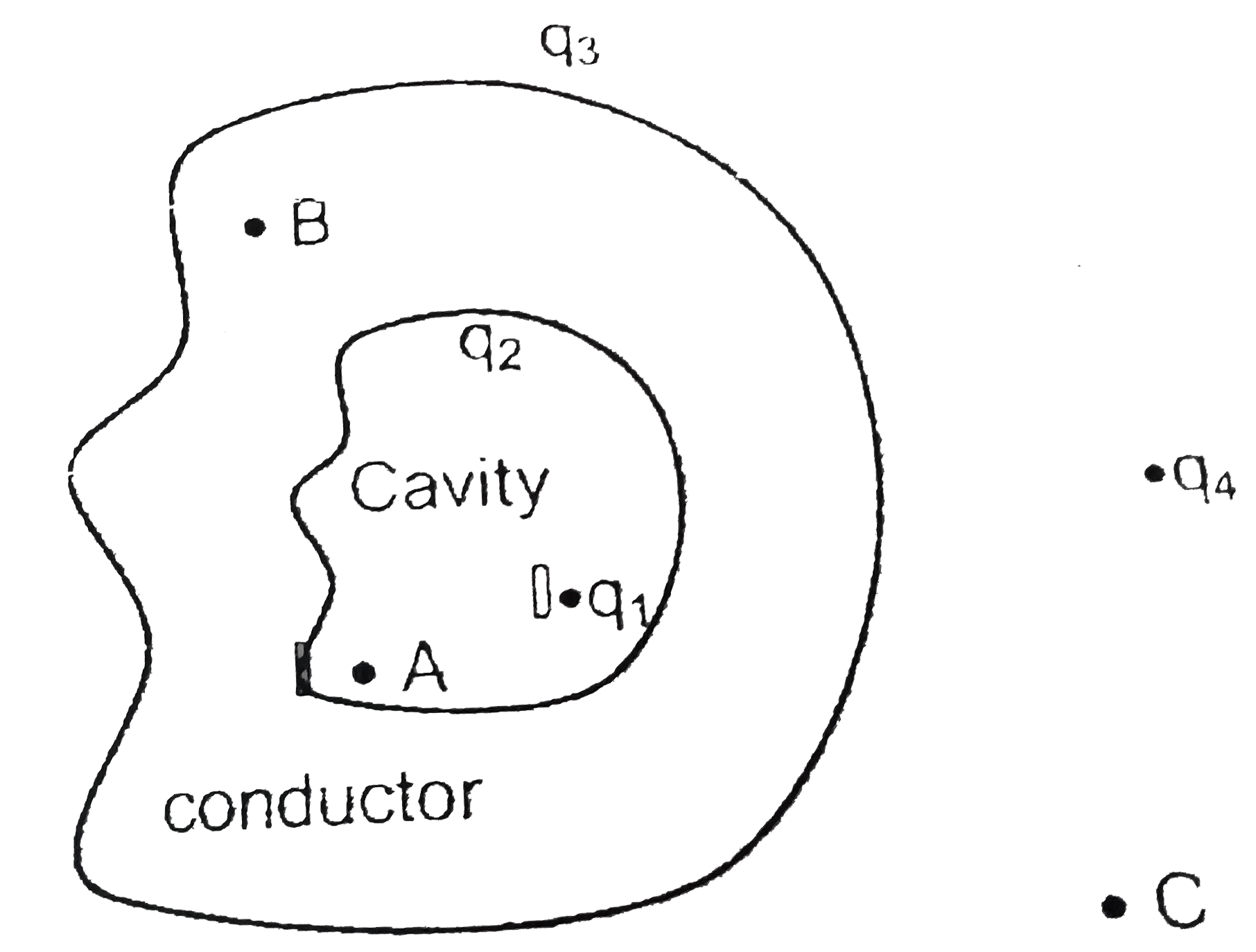
We have a fixed conductor having a cavity inside. There is a point charge q1 kept inside the cavity charge appearing at the inner surface of the cavity is q2. Charge appearing at outer surface of conductor is q3 and there lies another point charge q4 out side the conductor. Whole situation is shown in figure. q4. is held stationary by applying an external force →F0 on it. Three points A, B and C are shown. Answer the following two questions.
Q. If keeping the magnitude and nature of q1 fixed position of q1 is changed inside the cavity. Then choose the correct option(s)View Solution
We have a fixed conductor having a cavity inside. There is a point charge q1 kept inside the cavity charge appearing at the inner surface of the cavity is q2. Charge appearing at outer surface of conductor is q3 and there lies another point charge q4 out side the conductor. Whole situation is shown in figure. q4. is held stationary by applying an external force →F0 on it. Three points A, B and C are shown. Answer the following two questions.
Q. If keeping the nature and position of q1 fixed, magnitude of q1 is changed, then choose the INCORRECT options(s)View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.
 View Solution
View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.
 View Solution
View SolutionAn arrangement of three large metallic parallel plates with respective charges marked in figure is shown . What is the charge appearing on the left face of plate B ?
View SolutionFigure shows three concentric metallic spherical shells. The outermost shell has charge q2, the inner most shell has charge q1, and the middle shell is uncharged. The charge appearing on the inner surface of outermost shell is
View Solution

